Gage R&R für quantitative Daten in Excel - Anleitung
Dieses Tutorium zeigt Ihnen, wie Sie eine Messsystemanalyse (Gage R&R) (Nachvollziehbarkeit & Wiederholbarkeit) auf quantitativen Daten in Excel mithilfe der Statistiksoftware XLSTAT einrichten und interpretieren.
Datensatz für Messsystemanalyse (Gage R&R): Kontrollieren und validieren Sie Ihre Messmethode und -systeme, wenn Sie mehrere quantitative Messungen durch einen oder mehrere Prüfer an mehreren Teilen durchführen lassen
Die Messsystemanalyse (MSA) oder Gage R&R (Gage Repeatability und Reproducibility) ist ein Verfahren zum Überwachen und Beurteilen des Messprozesses. Es ist nützlich, um die für die Streuung der Messdaten verantwortlichen Quellen zu ermitteln. Die Streuung kann durch das Messgerät, den Prüfer und durch die Teile verursacht werden.
Das Wort „Gage" (oder Messgerät) geht darauf zurück, dass diese Methode darauf zielt ein Messgerät zu prüfen.
Eine Messung ist „wiederholbar", falls die Messungen eines bestimmten Prüfers für das gleiche Objekt (Produkt, Einheit, Teil oder Stichprobe je nach dem Anwendungsgebiet) wiederholt nicht weiter als ein vorgegebener Schwellwert variieren. Falls die Wiederholbarkeit eines Messsystems nicht befriedigend ist, sollte man die Qualität des Messinstrument in Frage stellen oder die Prüfer schulen, die keine wiederholbaren Ergebnisse erhalten, so fern man annehmen kann, dass das Messsystem nicht für die hohe Variabilität verantwortlich ist.
Eine Messung ist „reproduzierbar", falls die Messungen für ein bestimmtes Objekt (Produkt, Einheit, Teil oder Stichprobe je nach dem Anwendungsgebiet) von verschiedenen Prüfern nicht weiter als ein vorgegebener Schwellwert variiert. Falls die Reproduzierbarkeit eines Messsystems nicht befriedigend ist, so sollten die Prüfer geschult werden, damit die Ergebnisse homogener werden.
Das Ziel der Gage R&R Analyse ist es die Quellen der Variabilität zu identifizieren und notwendige Maßnahmen zur Reduktion einzuleiten, falls notwendig.
Wenn die Messwerte als quantitative Daten vorliegen, so stehen zwei alternative Methoden zur Gage R&R Analyse zur Auswahl. Die erste basiert auf der Varianzanalyse (ANOVA) und die zweite basiert auf R-Kontrollkarten (Bereich-Kontrollkarten).
Erstellen einer quantitativen Gage R&R-Analyse Im vorliegenden Beispiel wird die ANOVA-Methode verwandt, um das Messsystem zu beurteilen.
Nach dem Öffnen von XLSTAT, wählen Sie den Befehl XLSTAT / SPC / RRX.

Nach dem Klicken des Buttons erscheint das entsprechende Dialogfenster der Messsystemanalyse. Sie können nun die Daten im Excel-Blatt auswählen. Es gibt mehrere Arten die Daten in den XLSTAT Dialogfenstern auszuwählen (siehe auch das Tutoriel zu diesem Thema). Im untersuchten Beispiel beginnen die Daten in der ersten Zeile; es ist daher schneller die Spaltenauswahl zu benutzen. Daher erscheinen im Dialogfenster unten die Auswahlen in Form von Spalten. Die Option „Variablenbeschriftungen“ ist aktiviert, da die erste Zeile der Daten die Namen der Variablen enthält.
Wählen Sie die Spalte „Messwert“ als Y / Mass, die Spalte „Prüfer“ als X / Prüfer und die Spalte „Teil“ als Teile. Wählen Sie die Methode „ANOVA“

Im Reiter „Optionen“ wählen Sie „k Sigma“ als 6 und wählen Sie die gekreuzte ANOVA, um die Varianz in der Untersuchung als das 6fache der globalen Standardabweichung der Stichprobe zu wählen.

Im Reiter „Schätzung“ wird die Option „R-quer“ ausgewählt.

Im Reiter „Ausgabe“ werden alle Optionen aktiviert.

Im Reiter „Diagramme“ werden alle Optionen aktiviert.

Die Berechnungen beginnen, sobald der Button "OK" geklickt wird.
Interpretieren der Ergebnisse einer quantitativen Gage R&R-Analyse
Falls Sie in den Optionen von XLSTAT die Option „Auswahl bestätigen lassen“ aktiviert haben, so bittet Sie XLSTAT die Anzahl der Zeilen und der Spalten der Auswahlen zu bestätigen.
Das erste Ergebnis sind Varianzkomponenten der Daten mit zugehöriger Grafik. Man erkennt, dass der größte Anteil der Varianz ist auf Unterschiede zwischen den Teilen zurückzuführen ist (96.4 % Beitrag zur Varianz). Das Messsystem hat einen sehr geringen Anteil an der Gesamtvarianz (3.6%) und kann daher als angemessen bezeichnet werden.

Die folgenden Tabellen geben Einzelheiten über die Aufteilung der Streuung und von den daraus abgeleiteten Kennzahlen an. Eine Tabelle mit den Werten der Streuung der Untersuchung (basiert Faktor k Sigma der vom Benutzer hier als 6 gewählt wurde).
Darüber hinaus sind Kennzahlen zur Beurteilung der Messsystems angeben.

Wurde wie in diesem Beispiel die ANOVA-Methode ausgewählt, so werden die Ergebnisse der ANOVA mit den Anpassungskoeffizienten und der Tabelle der Varianzanalyse angezeigt.

Die folgenden Tabellen mit ihrem zugehörigen Diagramm stellen die Kontrollkarte X-quer mit den verschiedenen Kontrollgrenzen und Zentrallinien dar.
In einer ersten Tabelle werden die Daten der X-quer Kontrollkarte mit dem Gruppenmittelwert, Gruppenminimum und Gruppenmaximum angezeigt. Darüber hinaus sind noch die Zentrallinie (CL), die untere (LCL) und obere (UCL) Kontrollgrenze sowie die unteren und oberen Zonengrenzen A und B für jede Gruppe angegeben.
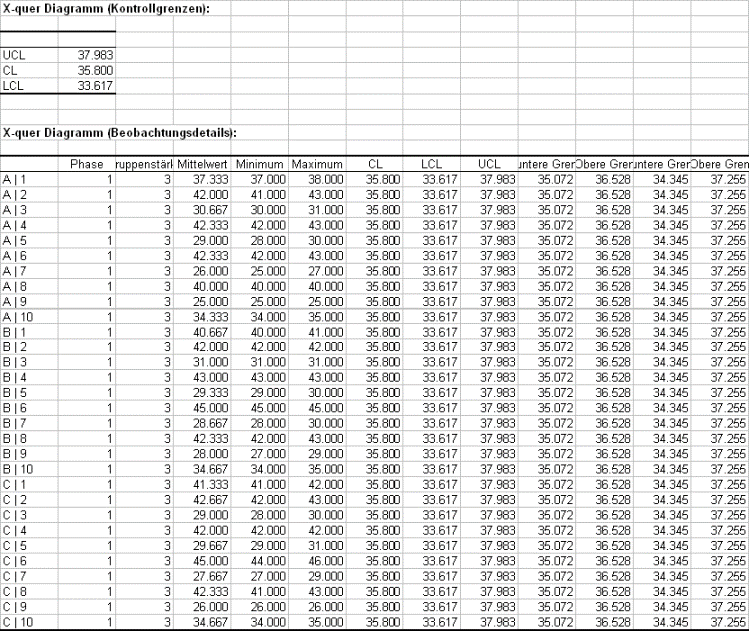
Zusammenfassend kann man dies auch in der Kontrollkarte X-quer sehen. Die Mittelwerte liegen nicht zwischen dem unteren und oberen Kontrollgrenzen. Die Varianz zwischen den einzelnen Teilen ist deutlich nicht unter Kontrolle.

In der gleichen Weise sind auch die Daten des R Diagramms zu lesen. Sie liegen allesamt innerhalb der Kontrollgrenzen. Dies ist ein typisches Ergebnis eines gültigen Messsystems.

Die beiden Kontrollkarten lassen daher den Schluss zu, dass das Messsystem fähig ist.
Es folgen nun Diagramme mit Box-Plots und Scatterdiagrammen pro Teil und pro Prüfer. So kann man die unterschiedlichen Verteilungen visuell vergleichen.
Man kann erneut feststellen, dass die Varianz zwischen den Teilen sehr groß ist. Die Teile 2, 4, 6 und 8 weisen deutlich höhere Messwerte als die Teile 3, 5, 7 und 9 auf.

Die Streuung zwischen den Prüfern dagegen ist sehr gering. Man kann visuell keine Unterschiede feststellen.

Abschließend werden die Mittelwertprofile pro Teil, pro Prüfer und pro Teil*Prüfer dargestellt.
Im Mittelwertdiagramm der Teile kann man die unterschiedlichen Teilegruppen wiederfinden.
Im Mittelwertdiagramm der Prüfer kann man leichte Unterschiede zwischen den Prüfern feststellen, diese sind jedoch gering im Vergleich zu den Unterschieden zwischen den Teilen 10-mal geringer.
In den beiden Profildiagrammen der Interaktion Teil*Prüfer kann man erneut feststellen das die Profile der Prüfer pro Teil sehr eng beieinander liegen, jedoch die Profile der Teile pro Prüfer auseinandergehen.

War dieser Artikel nützlich?
- Ja
- Nein