Einfache Simulationsmodelle in Excel - Anleitung

Dieses Tutorium zeigt Ihnen, wie Sie ein einfaches Simulationsmodell in Excel mithilfe der Statistiksoftware XLSTAT einrichten und interpretieren.

Simulationsmodelle erlauben es Informationen wie Mittelwert oder Median über Variablen zu erhalten, deren Werte nicht genau bekannt sind deren Verteilung jedoch bekannt oder geschätzt werden kann. Wenn einige „Ergebnis-Variablen“ von den „Verteilungs-Variablen“ durch eine genau bekannte oder unterstellte Formel abhängig sind, dann haben diese „Ergebnis-Variablen“ ebenfalls eine Verteilung. Sim erlaubt es Verteilungen zu definieren und dann mittels Simulation und eine empirische Verteilung der Ausgangs- und Ergebnisvariablen als auch über die zugehörigen Statistiken zu erhalten.

Simulationsmodelle finden heute Anwendung in vielen Gebieten wie Finanz und Versicherung, Medizin, Öl- und Gasprospektion, Buchhaltung oder Absatzplanung.

Zu Erstellung eines Simulationsmodells stehen Ihnen in XLSTAT die folgenden vier Bausteine zur Verfügung:

Verteilungen sind Zufallsvariablen zugeordnet. XLSTAT gibt einen die Wahl zwischen mehr als 20 Verteilungen, um die Ungewissheit der Werte, die die Variable annehmen kann, zu beschreiben (siehe Kapitel Definition einer Verteilung für mehr Details). Beispielsweise kann eine Trianguläre Verteilung gewählt werden, falls bekannt ist, dass die Werte zwischen zwei Grenzen variieren und ein wahrscheinlichster Wert (Modus) existiert. In jeder Iteration der Berechnung des Simulationsmodells wird eine zufällige Ziehung für jede definierte Verteilung durchgeführt.

Szenariovariablen erlauben das Modellieren eines Parameters der während des Simulationsmodells fix ist, außer während der Tornado- und Spinnenanalyse, in der sie zwischen zwei Grenzen variieren kann.

Ergebnisvariablen entsprechen den Ergebnissen oder Outputs des Modells. Sie hängen entweder direkt oder indirekt mittels einer oder mehreren Excelformeln von den Zufallsvariablen ab, denen Verteilungen zugeordnet sind, und falls vorhanden ebenfalls von Szenariovariablen. Das Ziel der Berechnungen des Simulationsmodells ist es die Verteilung der Ergebnisvariablen zu.

Statistiken erlauben das Verfolgen einer vorgegebenen Statistik einer Ergebnisvariablen. Zum Beispiel kann die Standardabweichung einer Ergebnisvariablen verfolgt werden.

Ein sinnvolles Modell sollte mindestens eine Verteilung und ein Ergebnis enthalten. Modelle können beliebig viele dieser Bausteine enthalten.

Sie können ein Modell entweder auf ein Excelblatt beschränken oder die gesamte Excelmappe benutzen.

Im Rahmen dieses Tutoriels wird ein sehr einfaches Simulationsmodell erstellt mit zwei zufälligen Eingangsvariablen und einer Ergebnisvariablen, um die Grundlagen der Simulationsmodelle darzustellen. Weitere Tutoriels mit allen 4 Modellelementen und Optionen finden Sie hinter folgenden Links: Sim2, Sim3, and Sim4.

Unser Simulationsmodell behandelt die Verkäufe und Kosten eines Geschäfts. Der Erfolg ergibt sich aus der Differenz zwischen Verkäufen und Kosten. Auf Basis von historischen Daten der Kosten und Verkäufen, die mittels des Tool „Anpassen an eine Verteilung“ analysiert wurden, wurde ermittelt, dass die Kosten einer Normalverteilung (mu=120, sigma=10) und die Verkäufe einer Normalverteilung (mu=80, sigma=20) folgen (siehe auch Tutoriel Anpassung eines Wahrscheinlichkeitsgesetzes an Daten für weitere Details).

Gehen wir zunächst von dem statischen Modell aus mit Verkäufen von 120 und Kosten in Höhe von 80. Der Erfolg ergibt sich als Differenz zu 40. Ausgehend von diesem statischen Modell fügen wir nun die verschiedenen Modellvariablen ein:

Dies finden Sie im Excel Blatt Statisch.

Wählen Sie als aktive Zelle die erste Verteilungsvariable, die den Wert 120 als Betrag der Verkäufe enthält.

Nach dem Öffnen von XLSTAT, wählen Sie den Befehl XLSTAT/Sim/Definition einer Verteilung oder klicken Sie auf den entsprechenden Button in der Toolbar " Sim " (siehe unten).

Nach dem Klicken des Buttons erscheint das entsprechende Dialogfenster der Definition einer Verteilung. Sie können nun die Daten im Excel-Blatt auswählen. Wählen Sie die Excel-Zelle mit dem Inhalt „Verkäufe“ als Namen. Als Verteilung wählen wir Normalverteilung mit mu = 120 und sigma = 10.

Nach dem Klicken des Buttons „OK“ wird der entsprechende Aufruf auf die Funktion XLSTAT_SimDist in die aktive Zelle einfügt.

Sie können nun die zweite Verteilung für die Kosten analog vornehmen. Als Verteilung wählen wir Normalverteilung mit mu = 80 und sigma = 20. Hier das zugehörige Auswahlfeld:

Wählen Sie als aktive Zelle die Ergebnisvariable, die den Wert 40 und die Formel =B2-B3 enthält. Nun wird die Ergebnisvariable definiert. Wählen Sie den Befehl XLSTAT/Sim/Definition eines Ergebnisses oder klicken Sie auf den entsprechenden Button in der Toolbar " Sim ".

Nach dem Klicken des Buttons erscheint das entsprechende Dialogfenster der Ergebnisdefinition. Sie können nun die Daten im Excel-Blatt auswählen. Wählen Sie die Excel-Zelle mit dem Inhalt „Erfolg“ als Namen.

Nach dem Klicken des Buttons wird der entsprechende Aufruf auf die Funktion XLSTAT_SimRes in die aktive Zelle einfügt.

Dies finden Sie im Excel Blatt Modell.

Um die Simulation nun zu starten klicken, wählen Sie den Befehl XLSTAT/Sim/Sim — Start der Simulation oder klicken Sie auf den entsprechenden Button in der Toolbar " Sim ".

Nach dem Klicken des Buttons erscheint das entsprechende Dialogfenster der Simulation. Sie können nun die Daten im Excel-Blatt auswählen. Setzen Sie die Anzahl der Simulationen auf 1000.

Im Reiter Optionen wählen Sie die Parameter der Tornado- und Spinnenanalyse. Wählen Sie den zentralen Wert als Vorgabewert der Zelle. Wählen Sie 10 Datenpunkte im Intervall und wählen Sie ein Intervall von -10% bis +10% der Wertabweichung:

Die Berechnungen beginnen, sobald der Button "OK" geklickt wird. Falls Sie in den Optionen von XLSTAT die Option „Auswahl bestätigen lassen“ aktiviert haben, so bittet Sie XLSTAT die Anzahl der Zeilen und der Spalten der Auswahlen zu bestätigen.

Das erste Ergebnis ist eine Zusammenfassung des konstruierten Modells. Es sind Details der beiden Verteilungs- und der Ergebnisvariablen zu finden.

Die folgenden Tabellen geben Einzelheiten über die beiden Verteilungsvariablen. Es werden deskriptive Statistiken, ein Histogramm und Statistiken über die Intervall angegeben.

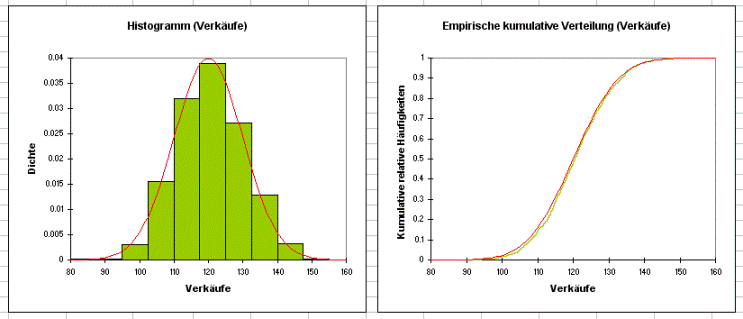
Die folgenden Tabellen geben die gleichen Einzelheiten über die Ergebnisvariablen. Es werden deskriptive Statistiken, ein Histogramm und Statistiken über die Intervall angegeben. Anschließend sind die Ergebnisse der Sensitivitäts-Analyse zu sehen.

Es schließt sich nun die Tornado-Analyse an.

Die Tornadoanalyse basiert nicht auf den Iterationen der Simulation, sondern auf einer Punkt-für-Punkt Analyse aller Ausgangsvariablen (Zufallsvariablen mit Verteilungen und Szenariovariablen).

Während der Tornado-Analyse wird für jede Ergebnisvariable, jede zufällige Ausgangsvariable und jede Szenariovariable einzeln untersucht. Ihre Werte werden dabei zwischen zwei Grenzen variiert und die Werte der Ergebnisvariablen werden gespeichert, um herauszufinden, wie jede zufällige und Szenariovariable die Ergebnisvariable beeinflusst. Für eine zufällige Variable können die angenommenen Werte entweder um den Median oder um den Vorgabewert der Zelle variieren. Die Grenzen können mittels Perzentilen oder Abweichungen definiert werden. Für eine Szenariovariable, wird die Analyse zwischen zwei bei der Definition der Szenariovariablen definierten Grenzen variiert. Die Anzahl der Punkte ist eine Option, die vom Benutzer vor Ausführen des Simulationsmodells bestimmt werden kann.

In einer Tabelle werden für die Verteilungen jeweils die maximale und minimale Veränderung des Ergebnisses und die sich daraus ergebende Bandbreite angezeigt. Im folgenden Diagramm wird sichtbar, dass die Kosten den stärksten Einfluss auf die Entwicklung des Erfolgs haben. Diese Ergebnisse basieren nicht auf den gesamten Simulationsiterationen.

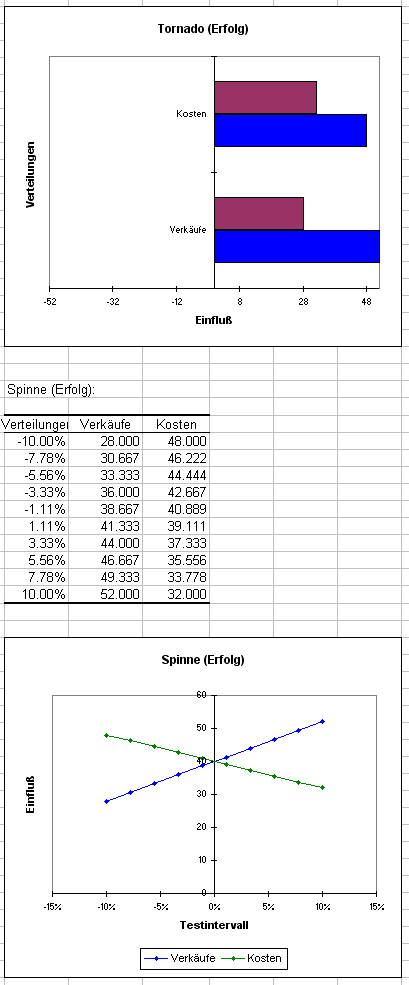
Abschließend wird die Korrelationsmatrix der verschiedenen Verteilungs- und Ergebnisvariablen angezeigt. Man sieht, dass Kosten und Verkäufe nicht korreliert sind. Jedoch der Erfolg mit Kosten und Verkäufen korreliert.