Prueba Kolmogorov-Smirnov: tutorial en Excel

Este tutorial le mostrará cómo ejecutar e interpretar una Prueba de Kolmogorov-Smirnov para comparar dos distribuciones en Excel usando XLSTAT.

¿No está seguro de si esta es la prueba estadística que está buscando? Consulte por favor esta guía.

Datos para ejecutar una prueba de Kolmogorov-Smirnov para comparar dos distribuciones

Los datos corresponden a las puntuaciones (0 - 30) usadas para medir la calidad de dos marcas de zapatos (marcas A y B). Las puntuaciones se calculan sobre la base de una encuesta dirigida a los clientes que usan ambas marcas. 15 clientes respondieron sobre la marca A y 8 clientes diferentes sobre la marca B.

Objetivo de este tutorial

Este tutorial se divide en dos partes: En la primera parte se comparan las distribuciones de las dos muestras sin hacer suposiciones sobre las distribuciones teóricas subyacentes (distribución normal, por ejemplo). Utilizamos la prueba no paramétrica de Kolmogorov-Smirnov, que es muy adecuada en este caso. En la segunda parte, utilizamos la prueba de Kolmogorov-Smirnov para comparar la distribución de una muestra con una distribución teórica.

Parte 1: Ejecución de una prueba de Kolmogorov-Smirnov en Excel para comparar dos distribuciones observadas

En este caso, estamos interesados en la comparación de las distribuciones de las dos muestras. En primer lugar, ¿cuál es la apariencia de estas distribuciones? Los histogramas son una buena herramienta para visualizar distribuciones continuas: XLSTAT / Visualización de datos / Histogramas. En la pestaña General, seleccione las dos muestras dentro del rango de celdas de datos. En la pestaña Opciones, active la opción mínima y escriba 0 en el cuadro. Esto obligará a los histogramas a tener el mismo límite inferior en el eje x haciendo más fácil compararlos. Haga clic en el botón OK.

Los histogramas aparecen en la hoja de resultados:

Sin hacer ninguna suposición teórica, podemos decir que la distribución de la muestra B está más sesgada hacia los valores bajos en comparación con la distribución de la muestra A. Utilizamos la prueba no paramétrica de Kolmogorov-Smirnov para comparar las dos distribuciones: XLSTAT / Pruebas no paramétricas / Comparación de dos distribuciones.

Seleccione la columna Marca A en la Muestra 1 y la columna de la marca B en la muestra 2. La prueba de Kolmogorov-Smirnov permite que las muestras sean desequilibrados como sucede en nuestros datos: la muestra B contiene un menor número de puntajes que la muestra A. En la pestaña Opciones, observe que es posible seleccionar una hipótesis alternativa de una cola y / o un cálculo exacto del valor p. En la pestaña Gráficos, activar la opción Histogramas acumulativos. Haga clic en el botón OK.

La hoja de resultados contiene el estadístico de Kolmogorov-Smirnov (0.475) que se puede extraer con facilidad (ver, más adelante, el gráfico de histogramas acumulativos). Este estadístico está asociado a un valor de p (0.133) que indica que las dos distribuciones no son significativamente diferentes con alfa = 0.05.

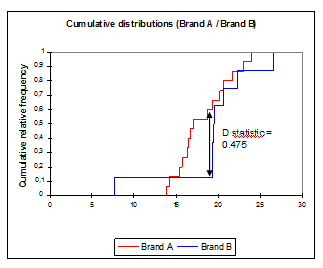
El gráfico de distribuciones acumulativas presenta la variable estudiada (resultados de la encuesta) en el eje x. Para un punto dado en el eje x, la frecuencia relativa acumulada de una marca es la proporción de resultados menores que ese punto entre las puntuaciones de la marca. Por lo tanto, como ya sugirieron los histogramas, la marca B parece comenzar a acumular puntuaciones antes que la marca A a lo largo del eje x. Echemos un vistazo a las medianas, que son las puntuaciones correspondientes a una frecuencia relativa acumulada de 0.5. La mediana de la marca B (~ 20) parece ser más alta que la mediana de la marca A (~ 17).

El estadístico D de Kolmogorov-Smirnov es la desviación más alta que se produce entre las dos curvas. En nuestro ejemplo, esta desviación cae dentro de la región de la mediana, pero este puede no ser necesariamente el caso cuando se utilizan otros datos. Cuanto mayor sea el estadístico D, menor es el valor de p y más significativa es la diferencia entre las dos distribuciones.

Parte 2: Ejecución de una prueba de Kolmogorov-Smirnov en Excel para comparar una distribución observada con una teórica

Supongamos que las puntuaciones de calidad de la marca A se obtuvieron en Francia. Para los clientes de Estados Unidos, este resultado sigue una distribución normal con una media de 21.5 y una desviación estándar de 2.3. Podemos preguntarnos si la distribución de las puntuaciones en Francia es significativamente diferente de la distribución teórica de las puntuaciones de los Estados Unidos. También en este caso, utilizamos la prueba de Kolmogorov-Smirnov. La única diferencia con la parte anterior es que nuestro objetivo es la comparación de una distribución observada con una teórica en lugar de comparar dos distribuciones diferentes.

Seleccionamos el comando XLSTAT / Pruebas no paramétricas / Ajuste de una distribución. En la pestaña General, seleccione los datos de la marca A, la distribución normal, active la opción Introducir e introduzca los siguientes parámetros: µ = 21.5 y sigma = 2.3. En la pestaña Gráficos, active la opción Histogramas acumulativos. Haga clic en el botón OK.

En la hoja de resultados, el histograma (abajo a la izquierda) muestra que la distribución observada se sitúa en valores bajos de puntuación en comparación con la curva teórica que refleja la distribución de puntuaciones de los Estados Unidos (línea roja).

La prueba de Kolmogorov-Smirnov se asocia a un valor de p de 0.000, lo que sugiere que la distribución observada es significativamente distinta de la teórica con alfa = 0.05.