Modèle Illness-Death paramétrique dans Excel

Ce tutoriel explique comment mettre en place et interpréter un modèle Illness-Death paramétrique dans Excel avec le logiciel XLSTAT.

Modèle Illness-Death

Le modèle Illness-Death est un modèle de survie à 3 états. Il permet d’observer la survie des individus et de modéliser l’évolution entre les différents états. Des variables explicatives peuvent être ajoutées au modèle pour évaluer l’effet de facteurs extérieurs sur la survie.

Ce modèle est basé sur l’estimation des paramètres par maximum de vraisemblance et s’applique à des données de survie, c’est-à-dire à des données temporelles éventuellement censurées et tronquées.

Jeu de données

Un extrait de 1000 individus choisis aléatoirement parmi les données Paquid est utilisé pour illustrer l’application du modèle Illness-Death. Les données Paquid ont été récoltées sur 3777 individus du sud-ouest de la France, âgés de 65 ans et plus, entre 1988 et 2018. L'un des principaux objectifs de cette collecte était de développer les recherches sur la démence et d’en déterminer certaines des causes notamment pour la maladie d'Alzheimer.

Le jeu de données contient 7 variables :

Les indicateurs d’état :

• démence : qui vaut
  * 1 si l’individu est dément,
  * 0 sinon.

• décès : qui vaut
  * 1 si l’individu est décédé,
  * 0 sinon.

Les données de dates (âges) :

• entrée : L’âge d’entrée dans l’étude

• gauche :
  * l'âge lors de la visite précédant le diagnostic de la démence si l’individu est dément,
  * l'âge de la dernière visite sinon.

• droite :
  * l'âge lors de la visite de diagnostic de la démence si l’individu est dément,
  * l'âge de la dernière visite sinon.

• fin : L’âge
  * de décès si l’individu est décédé,
  * de dernières nouvelles sinon.

La variable explicative :

• certif : qui vaut
  * 1 si l’individu n’a pas eu son certificat d’études primaires
  * 0 sinon.

L’âge des dernières nouvelles correspond à l’âge auquel l’individu a été vu pour la dernière fois.

L’objectif de ce tutoriel est de répondre aux questions suivantes :

• La démence augmente-t-elle le risque de décès ?

• La certification diminue-t-elle les chances d’être dément ?

Pour répondre à ces questions, il faut modéliser les transitions entre les états sain, dément et décès et évaluer l’impact de la certification sur ces transitions.

Paramétrer un modèle Illness-Death avec XLSTAT

Pour activer la boîte de dialogue du modèle Illness-Death, lancez XLSTAT, puis sélectionnez la commande XLSTAT / Fonctions Avancées / Analyse de survie / Modèle Illness-Death.

Dans l’onglet Général, sélectionnez la démence et le décès dans les Indicateurs d’états et les 4 âges dans les données de date :

Dans l’onglet Covariables, sélectionnez la variable qualitative certif du jeu de données.

L’option Différentes par transition permet de personnaliser les covariables selon les différentes transitions. En choisissant uniquement l’option Covariables, seule la variable « Certif » est évaluée sur toutes les transitions.

Les autres onglets de la boîte de dialogue permettent de paramétrer l’estimation et les sorties.

Dans l’onglet Options, paramétrez les critères de convergence, le nombre d’itérations et le temps maximum de calcul de l’algorithme d’optimisation.

Dans ce tutoriel, les valeurs par défaut de ces paramètres sont conservées.

Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.

Interpréter les résultats d'un modèle Illness-Death avec XLSTAT

Des statistiques générales sont d’abord affichées pour les données de temps et les indicateurs d’états :

Puis un résumé du nombre d’individus par transition est donné ressemblant à la figure ci-dessous.

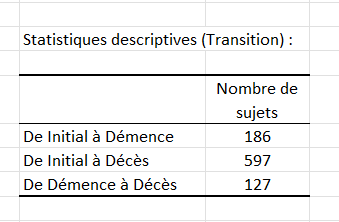
Sur ce tableau on observe que la plupart des individus décède sans être dément (597 individus).

Les deux tableaux suivants donnent les paramètres du modèle : les coefficients de régression associés aux variables explicatives et les paramètres de Weibull.

Dans le tableau des coefficients de régression, le test de Wald nous indique les p-valeurs de chaque variable pour chaque transition. Une variable influence une transition si son effet est significativement non nul c’est-à-dire si sa p-valeur est inférieure au seuil alpha = 0.05, choisi dans l’onglet Options.

On déduit que seulement la première transition « Etat Initial --> Etat Dément » est influencée par la certification car sa p-valeur = 0.010 < 0.05. La certification a donc un impact sur la démence, mais pas sur la mortalité.

Maintenant que nous avons prouvé qu’il existe un lien entre la certification et la démence il faut en déterminer la nature : est-ce que la certification favorise ou défavorise la démence ?

Dans un modèle Illness-Death, la valeur des coefficients classiques est difficile à interpréter. On s’intéressera plutôt au rapport de risque (l’exponentielle du coefficient). Il s’interprète comme un risque relatif des individus non certifiés sur ceux qui le sont.

• HR = 1 : Pas d’effet / Même risque,

• HR < 1 : Risque réduit / Un individu non-certifié a un risque plus faible qu’un individu certifié,

• HR > 1 : Risque augmenté / Un individu non-certifié a un risque plus élevé qu’un individu certifié.

Pour la première transition les individus non certifiés ont 0.597 fois plus de chances d’être déments que les individus certifiés. Dans ce cas, on peut dire que la certification favorise la démence puisque le risque des individus non-certifiés est réduit.

Dans le tableau des paramètres de Weibull, on a pour chaque transition les paramètres de forme et d’échelle de Weibull.

Grâce aux paramètres de Weibull, on peut calculer les intensités de transition de base :

Grâce au graphique des intensités de transition, on observe que le risque de démence et de décès augmente avec l’âge puisque toutes les courbes sont croissantes. On observe également que le risque de décès pour un individu malade, représenté en bleu, est plus important que le risque de décès pour un individu en bonne santé, représenté en rouge. Enfin, en regardant la courbe noire, on observe que le risque de démence augmente fortement à partir de 90 ans.

D’autres quantités, autres que les intensités de transition, peuvent être analysées. Les probabilités de transition et les fonctions de survie peuvent ajouter de l’information et permettent une interprétation plus naturelle.

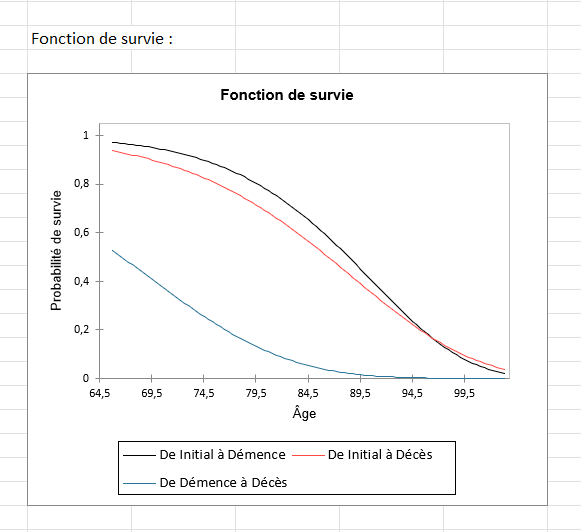
Notez que la courbe de survie, en noir, ne correspond pas à la survie dans le sens commun du terme (probabilité d’être toujours en vie) mais à la survie ou probabilité d’être en bonne santé (en vie et non malade).

Finalement, cette étude apporte plusieurs informations. Tout d’abord, la certification a un effet significatif sur le risque de démence. Plus particulièrement, les individus ayant obtenu une certification des études primaires sont davantage touchés par la démence que les individus sans certification. On a également pu montrer qu’un individu atteint de démence à une survie plus faible qu’un individu sain et qu’à partir de l’âge de 90 ans le risque de démence augmente fortement.