Nichtparametrische Regression (kernel & lowess) in Excel
Dieses Tutorium wird Ihnen helfen, eine a nichtparametrische Regression (Kernel/Lowess) in Excel mithilfe der XLSTAT Software einzurichten und zu interpretieren. Sie sind nicht sicher, ob es sich hierbei um die Modellierungsfunktion handelt, nach der Sie suchen? Weitere Hinweise finden Sie hier.
Was ist Kernel-Regression?
Die Kernel Regression ist ein Tool der Modellierung, das gleichzeitig Teil der Familie der Glättungsmethoden ist. Im Gegensatz zur linearen Regression, die mit einem erklärenden und vorhersagendem Ziel betrieben wird (Verständnis eines Phänomens und seine anschließende Vorhersage) , so ist die Kernel regression unter den nicht parametrischen Regressionsmethoden erfasst mit überwiegendem Vorhersagecharakter.
Die Kernel Regression gehört zur Familie der nichtparametrischen Regressionsmethoden. Die Kernel Regression gliedert sich in drei Phasen auf:
- Eine Anpassungsetape während derer man versucht die beste Kombination eines Modelltyps, einer Kernelfunktion und einer Bandbreite auf Basis einer Teststichprobe zu finden.
- Eine Bestätigungsphase die es erlaubt das Modell an neuen Beobachtungen zu überprüfen für die Vorhersagewerte bekannt sind;
- Eine Anwendungsphase, in der das Modell auf einen neuen Datensatz angewendet wird, für den die Vorhersagewerte unbekannt sind.
Bemerkung: Die nichtparametrische Regression beinhaltet eine Bestätigungsphase, da eine bestimmte Beobachtung niemals zum Erstellen des Modells benutzt wird, das die zugehörige Vorhersage erzeugt. Jedoch ist es jederzeit möglich, eine Unterstichprobe zu isolieren, die ausschließlich zur Bestätigungsphase des Modells eingesetzt wird, um die Robustheit des Modells zu überprüfen.
Im Gegensatz zur linearen Regression, die mit einem erklärenden und vorhersagendem Ziel betrieben wird (Verständnis eines Phänomens und seine anschließende Vorhersage) , so ist die Kernel regression unter den nicht parametrischen Regressionsmethoden erfasst mit überwiegendem Vorhersagecharakter. Die Modellstruktur ist wirklich variabel und komplex, ähnlich einem Filter oder einer Black Box. Es existieren zahlreiche Varianten der Kernel regression.
Daten für die Kernel-Regression
Das in diesem Tutorial behandelte Beispiel entspricht einem sehr einfachen Fall, der nur von illustrativen Interesse ist. Die nichtparametrische Regression kann von großen Nutzen sein, um komplexe Phänomene vorherzusagen, wie Zeitreihen im Finanzwesen, Luftverschmutzung von einem Tag auf den anderen oder Verkaufszahlen von Quartal zu Quartal. Sie wird ebenfalls manchmals zum Glätten einer Zeitreihe eingesetzt.
Das Beispiel benutzt die gleichen Daten wir das Tutorial über die lineare Regression.
Nach dem Öffnen von XLSTAT, wählen Sie den XLSTAT/Modellieren der Daten/Nichparametrische Regression Befehl oder klicken Sie auf den entsprechenden Button der "Modellierung der Daten" Toolbar (siehe unten).

Nach den Klicken des Bouttons erscheint das Dialogfenster der nichtparametrischen Regression. Sie können nun die Daten auf dem Excel-Blatt auswählen. Die "Ahängige Variable" entspricht der Variablen, die erklärt werden soll (oder der Variable, die modelliert werden soll). In diesem Fall ist es das Gewicht. Die erklärenden Variablen sind die Größe und das Alter (quantitative Daten) und das Geschlecht (qualitative Daten). Die Auswahlen werden spaltenweise durchgeführt, da die Daten in der ersten Zeile beginnen. Die Option "Beschriftung der Variablen" ist aktiviert, da die erste Zeile den Namen der Variablen entspricht. Hier wird eine Polynomielle Funktion ersten Grades mit alle Daten (außen denen die zur Vorhersage bestimmt sind), einer Gewichtung auf Basis des Gauß-Kernels und einer Bandbreite basierend auf der Standardverteilung der Variablen gewählt. Letztere erlaubt es Skaleneffekte während der Berechnungen zu vermeiden.
Bemerkung: Die Methode ist einem ANCOVA Modell sehr verwandt, der Unterschied besteht darin, dass man eine Beobachtung nicht im Modell benutzt um die zugehörige Vorhersage zu treffen und darin dass die Gewichtung der Beobachtungen im Modell von ihrem Abstand zu der vorherzusagenden Beobachtung abhängen.

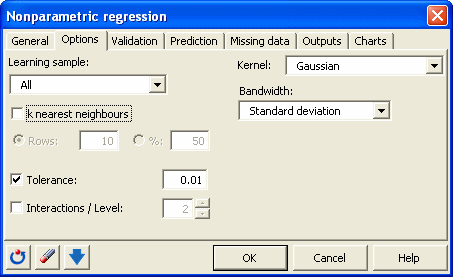

Die Berechnungen beginnen, sobald der Button OK geklickt wurde.
Interpretieren der Ergebnisse einer Kernel-Regression
Die Ergebnisse werden angezeigt. Die Koeffizienten der Anpassungsgüte erlauben es die Performanz des Modells zu beurteilen und mehrere Modelle zu vergleichen. Die R’² (der Bestimmungskoeffizient) gibt eine Idee des %-Satzes der Variabilität der Gewichtsvariablen, die durch die erklärenden Variablen erklärt wird. Je näher R’² bei 1 liegt, desto besser ist das Modell.
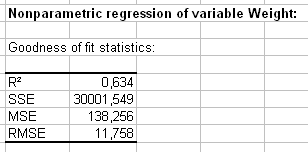
Die Tabelle der Vorhersagen und Residuen erlaubt es für jedes Individuum die Ausgangsdaten, die Vorhersage und das Residuum zu betrachten. Die Residuen variieren in absoluten Werten zwischen 0.01 (Individuum 45) und 40 (Individuum 195). Bei den Valdierungsdaten im zweiten Teil der Tabelle bemerkt man, dass die Residuen stark variieren. Für die Individuen 229 und 235 sind die Vorhersagen ausgezeichnet. Es ist um einiges schlechter für das Individuum 224.

War dieser Artikel nützlich?
- Ja
- Nein