Monotone Regressionen (MONANOVA) in Excel

Dieses Tutorium zeigt Ihnen, wie Sie eine Monotone Regression (MONANOVA) in Excel mithilfe der Statistiksoftware XLSTAT entwerfen und interpretieren.

Monotone Regression-MONANOVA-Methode

Die Monotone Regression und die MONANOVA-Methode unterscheiden sich nur durch die Tatsache, dass die erklärenden Variablen entweder quantitativ oder qualitativ sind. Diese Methoden basieren auf iterativen Algorithmen, die auf dem ALS-Algorithmus (alternierende kleinste Quadrate) basieren. Ihr Prinzip ist einfach: Sie bestehen aus einer Alternierung zwischen einer gewöhnlichen linearen Regression oder ANOVA und einer monotonen Transformation der abhängigen Variablen (nach Ermitteln der optimalen Skalierung).

Der MONANOVA-Algorithmus wurde von Kruskal (1965) eingeführt. Monotone Regressionsmethoden und die Arbeit am ALS-Algorithmus gehen zurück auf Young et al. (1976).

Diese Methoden werden häufig als Teil der Conjoint-Analyse mit vollständigem Profil verwendet. XLSTAT kann sie innerhalb einer Conjoint-Analyse, aber auch unabhängig anwenden.

Das Tool für die monotone Regression (MONANOVA) kombiniert eine monotone Transformation der Antwortvariablen mit einer linearen Regression, um die Ergebnisse der Regression zu verbessern.

Datensatz für die MONANOVA-Methode (monotone Regression)

Absicht dieser MONANOVA-Analyse

Mithilfe der MONANOVA-Methode möchten wir herausfinden, wie das Gewicht der Kinder in Abhängigkeit von ihrem Geschlecht, (eine qualitative Variable, die den Wert f oder m annimmt), ihrer Größe und ihrem Alter variiert, und überprüfen, ob eine monotone Transformation die Qualität des Modells verbessert.

Anders als bei einem linearen Modell kombiniert sie eine monotone Transformation der abhängigen Variablen mit einer gewöhnlichen Kleinste Quadrate Regression. Sie basiert auf einem iterativen Algorithmus, der zwischen einem allgemeinen linearen Modell (GLM) und einer monotonen Transformation alterniert, um die Qualität der Vorhersage zu verbessern.

Einrichten einer MONANOVA

Nach dem Öffnen von XLSTAT wählen Sie den Befehl XLSTAT/CJT/MONANOVA oder klicken Sie auf den entsprechenden Button der Symbolleiste XLSTAT-CJT (siehe unten).

Nach dem Klicken des entsprechenden Buttons erscheint das Dialogfenster MONANOVA. Markieren Sie die Daten in dem Excel-Tabellenblatt. Die abhängige Variable (oder zu modellierende Variable) ist hier das Gewicht.

Die quantitativen erklärenden Variablen sind Größe und Alter. Die qualitative Variable ist das Geschlecht. Da wir den Spaltennamen für die Variablen ausgewählt haben, lassen wir die Option Variablenbeschriftungen aktiviert. Bei den anderen Optionen wurde der Vorgabewert beibehalten.

Die Berechnungen beginnen, sobald Sie auf OK geklickt haben. Die Ergebnisse werden dann angezeigt.

Interpretieren der Ergebnisse einer MONANOVA-Analyse

Die erste Tabelle zeigt die Anpassungskoeffizienten des Modells an. Der R² (Bestimmtheitskoeffizient) zeigt den Prozentsatz der Variabilität der abhängigen Variablen an, was durch die erklärenden Variablen erklärt wird. Je näher der R² an 1 liegt, desto besser ist die Anpassung.

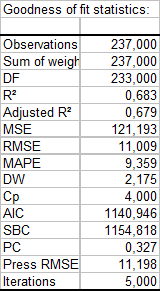
In diesem besonderen Fall werden 68 % der Variabilität des Gewichts durch die Größe, das Alter und das Geschlecht erklärt. Die restliche Variabilität ist auf einige Effekte (andere erklärende Variablen), die während dieses Experiments nicht gemessen wurden oder nicht gemessen werden konnten, zurückzuführen. Wir können raten, dass bestimmte genetische und ernährungstechnische Effekte involviert sind.

Als Teil der MONANOVA-Methode wird eine Tabelle mit zusätzlichen Anpassungstests angezeigt. Diese Tests ermöglichen das Erreichen von Grenzen des p-Werts des Modells.

Es ist wichtig, die Ergebnistabelle der Varianzanalyse zu untersuchen (siehe unten). Die Ergebnisse ermöglichen es uns festzustellen, ob die erklärenden Variablen signifikante Informationen (Nullhypothese H0) für das Modell liefern oder nicht. In anderen Worten, sie bieten Ihnen die Möglichkeit, sich selbst zu fragen, ob es gültig ist, den Mittelwert zum Beschreiben der Gesamtpopulation zu verwenden, oder ob die von der erklärenden Variablen gelieferten Informationen nützlich sind oder nicht.

Der Fishers F-Test wird verwendet. Angesichts der Tatsache, dass die Wahrscheinlichkeit entsprechend dem F-Wert niedriger als 0,0001 ist, bedeutet das, dass wir einen niedrigeren Risikowert als 0,01 % für die Annahme, dass die Nullhypothese (keine Auswirkung auf die beiden erklärenden Variablen) falsch ist, verwenden würden. Daher können wir mit Sicherheit daraus schließen, dass die drei Variablen eine signifikante Menge an Informationen liefern.

Die folgende Tabelle liefert Details zum Modell. Diese Tabelle ist hilfreich, wenn Vorhersagen erforderlich sind oder wenn Sie die Koeffizienten des Modells für eine gegebene Population mit den für eine andere Population erhaltenen vergleichen möchten. Wir können sehen, dass der p-Wert für den Geschlechtsparameter 0,69 ist, und dass der entsprechende Konfidenzbereich 0 beinhaltet. Dies bestätigt den schwachen Einfluss des Geschlechts auf das Modell. Wenn wir uns den Parameter ansehen, der dem Geschlecht-w entspricht, scheint es, dass für ein bestimmtes Alter und eine bestimmte Größe eine geringe Gewichtszunahme bei Mädchen festzustellen ist.

Das nachstehende Diagramm liefert die Analyse der durchgeführten monotonen Transformation.

Wir sehen, dass die Transformation nahe an der linearen Transformation liegt. Dies bringt uns dazu, die Ergebnisse mit denen einer Kovarianzanalyse (ANCOVA) des linearen Modells zu vergleichen. Die Ergebnisse in Zusammenhang mit dieser Analyse stehen im Tabellenblatt ANCOVA zur Verfügung. Wir sehen, dass der R² 0,63 ist. Dieser Wert ist niedriger als beim transformierten Modell, aber die Differenz ist nicht sehr wichtig.

Daraus folgt, dass der Umfang des Effekts der monotonen Transformation nicht viele zusätzliche Informationen über die Qualität der Modellvorhersage liefert. Die erklärenden Variablen haben immer noch signifikante Einflüsse und wir können sagen, dass eine lineare Beziehung im Modell besteht.