Régression monotone / MONANOVA dans Excel
Ce tutoriel explique comment calculer et interpréter une Régression monotone / MONANOVA avec Excel en utilisant XLSTAT.
La régression monotone - La méthode MONANOVA
La régression monotone et la méthode MONANOVA diffèrent uniquement dans le fait que les variables explicatives sont soit quantitatives, soit qualitatives. Ces méthodes sont basées sur des algorithmes itératifs issus de l’algorithme ALS (moindres carrés alternés). Leur principe est simple, il consiste en l’alternance entre une estimation classique du type régression linéaire ou ANOVA et d’une transformation monotone des variables dépendantes (issue des recherches sur l’optimal scaling).
L’algorithme MONANOVA a été présenté par Kruskal (1965). Les méthodes de régression monotone et les travaux sur l’algorithme ALS sont quant à eux dus à Young et al. (1976).
Ces méthodes sont utilisées couramment dans le cadre de l’analyse conjointe basée sur les profils complets. XLSTAT-Conjoint permet de les appliquer à l’intérieur d’une analyse conjointe mais aussi de manière indépendante.
L’outil régression monotone (MONANOVA) permet de combiner une transformation monotone des réponses à une régression linéaire de manière à améliorer les résultats de la régression.
Jeu de données pour la méthode MONANOVA (régression monotone)
Les données proviennent de Lewis T. and Taylor L.R. (1967). Introduction to Experimental Ecology, New York: Academic Press, Inc.. Elles concernent 237 enfants, décrits par leur sexe, leur âge en mois, leur taille en inch (1 inch = 2.54 cm), et leur poids en livres (1 livre = 0.45 kg).
But de ce tutoriel sur la méthode MONANOVA
En utilisant la méthode MONANOVA, notre but est d'étudier comment le poids varie en fonction du sexe (variable qualitative prenant la valeur f ou m), de l'âge et de la taille de l'enfant, et de vérifier si une transformation monotone de la variable poids améliore la qualité du modèle.
La méthode MONANOVA (régression monotone) est une méthode proche de la régression linéaire ou de l'ANOVA, elle permet de modéliser une relation entre une variables dépendante quantitatives et des variables explicatives quantitatives ou/et qualitatives. A la différence d'un modèle linéaire, elle combine une transformation monotone de la variable dépendante à la méthode des moindres carrés. Elle est basée sur un algorithme itératif alternant entre un modèle linéaire général (GLM) et une transformation monotone permettant d'améliorer la qualité de prédiction.
Paramétrer une analyse MONANOVA
Une fois XLSTAT lancé, choisissez la commande XLSTAT-CJT/ MONANOVA (régression monotone) ou cliquez sur le bouton MONANOVA de la barre d'outils XLSTAT-CJT.

Une fois le bouton cliqué, la boîte de dialogue correspondant à la MONANOVA apparaît.
Vous pouvez alors sélectionner les données sur la feuille Excel.
La Variable dépendante correspond à la variable expliquée (ou variable à modéliser), qui est dans ce cas précis le "poids".
Les variables quantitatives explicatives sont ici la "taille" et l'"âge", tandis que la variable qualitative est le "sexe".
L'option Libellés des variables est laissée activée car la première ligne des colonnes comprend le nom des variables.
Les options des autres onglets sont laissées à leur valeur par défaut.

Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.
Interpréter les résultats d'une MONANOVA ou régression monotone
Le premier tableau de résultats fournit les coefficients d'ajustement du modèle. Le R² (coefficient de détermination) donne une idée du % de variabilité de la variable à modéliser, ici le poids, expliquée par les variables explicatives. Plus ce coefficient est proche de 1, meilleur est le modèle.

Dans notre cas, 68% de la variabilité est expliquée par la taille, l'âge et le sexe. Le reste de la variabilité est dû à des effets (autres variables explicatives) qui n'ont pas été mesurés ou mesurables au cours de l'expérience. Des effets génétiques et nutritifs sont de toute évidence impliqués, mais néanmoins une recherche plus poussée pourrait donner de meilleurs résultats.
Dans le cadre de la méthode MONANOVA, un tableau de tests d'ajustement supplémentaires est affiché. Ces tests permettent d'obtenir des bornes sur la p-valeur du modèle.

Les p-valeurs obtenues étant petite on peut dire que l'impact des variables explicatives est différent de 0.
Le tableau d'analyse de la variance est un résultat qui doit être analysé attentivement (voir ci-dessous). C'est à ce niveau que l'on teste si l'on peut considérer que les variables explicatives sélectionnées (la taille et le poids) apportent une quantité d'information significative au modèle (hypothèse nulle H0) ou non. En d'autres termes, c'est un moyen de tester si la moyenne de la variable à modéliser (le poids) suffirait à décrire les résultats obtenus ou non.
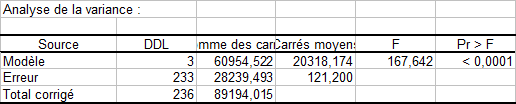
Le test du F de Fisher est utilisé. Étant donnée que la probabilité associée au F est dans ce cas inférieure à 0.0001, cela signifie que l'on prend un risque de se tromper de moins de 0.01% en concluant que les variables explicatives apportent une quantité d'information significative au modèle.
Le tableau suivant fournit les détails sur le modèle et est essentiel dès lors que le modèle doit être utilisé pour faire des prévisions, des simulations ou s'il doit être comparé à d'autres résultats. Nous voyons que la p-value associé au test de Student pour le sexe est de 0.698, et que l'intervalle de confiance à 95% associé au sexe comprend la valeur 0. Cela confirme le faible impact du sexe sur le modèle. Si l'on s'en tient à la valeur du paramètre associé au sexe féminin, il semblerait que pour une taille et un âge donnés, le fait d'être une fille ait un impact légèrement positif sur le poids.

Le graphique plus bas permet d'analyse la transformation monotone effectuée.

On voit que la transformation est proche de la transformation linéaire. Ceci nous pousse à comparer les résultats à ceux d'un modèle linéaire appliqué avec l'analyse de covariance (ANCOVA) ,les résultats associés à cette analyse sont disponibles dans la feuille ANCOVA. On voit que le R² est de 0,63. Celui-ci est moins élevé que pour la modèle transformé mais la différence n'est pas très importante.
En conclusion, la transformation monotone de la taille n'apporte pas beaucoup d'informations supplémentaires sur la qualité de prédiction du modèle. Les variables explicatives ont toujours des impacts significatifs et on peut dire qu'il existe une relation linéaire dans le modèle.
Cet article vous a t-il été utile ?
- Oui
- Non