ANOVA unifactorial y comparaciones múltiples en Excel
Este tutorial le mostrará cómo configurar e interpretar un Análisis de Varianza (ANOVA) unifactorial (One-way Analysis of Variance) seguido de comparaciones múltiples de Tukey & Dunnett en Excel usando el software XLSTAT.
Datos para ejecutar un ANOVA unifactorial
Los datos corresponden a una experiencia en que 4 dentàfricos fueron probados, cada uno, en 6 personas con el fin de medir su impacto sobre la blancura de los dientes. Todos los pacientes utilizaban antes el mismo dentàfrico.
Objetivo de este tutorial
En utilizar la herramienta del ANOVA function de XLSTAT, aquà buscamos a determinar si existe una diferencia significativa entre los diferentes dentàfricos, y si es asà, cual seria el más eficaz. Estamos en un caso de ANOVA de un factor (la clase de dentàfrico) equilibrado ya que el número de repeticiones es el mismo para los diferentes grupos.
Configuración de un ANOVA unifactorial
-
Abra XLSTAT.
-
Seleccione el comando XLSTAT / Modelado de datos / ANOVA. Una vez que haya hecho clic en el botón, aparecerá el cuadro de diálogo de ANOVA.
-
Seleccione los datos en la hoja de Excel. La variable dependiente corresponde aquí a la "Blancura", cuya variabilidad deseamos explicar por el efecto de la fórmula de "Pasta de dientes", siendo esta última la variable explicativa cualitativa.
-
Asegúrese de marcar la opción Etiquetas de variables.
-
En este ejemplo, queremos mostrar los resultados en la misma hoja donde están almacenados los datos, por lo que elegimos la opción Rango y seleccionamos la celda que corresponde a la esquina superior izquierda del informe de resultados que se mostrará.
En XLSTAT, es posible seleccionar los datos de dos maneras diferentes para la ANOVA. La primera es en forma de columnas, una columna para la variable dependiente y otra para la variable explicativa.
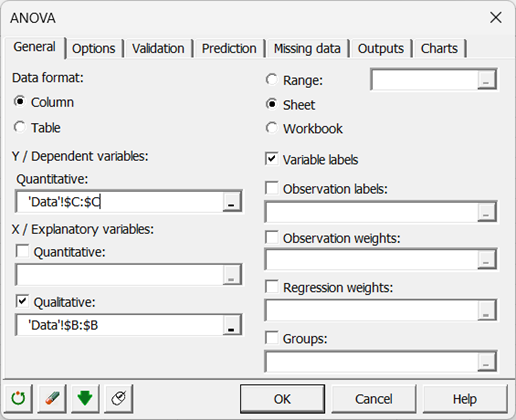
La segunda forma de seleccionar los datos es en forma tabular, con cada columna representando una modalidad de la variable explicativa.
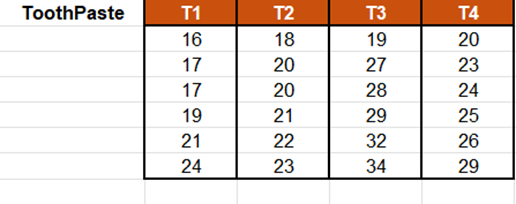
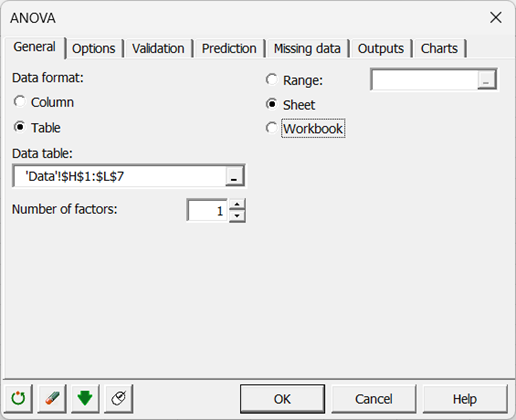
-
En la pestaña Opciones, deje la opción de restricción en a1=0. Esto significa que deseamos que el modelo se construya bajo la suposición de que la pasta de dientes T1 tiene el efecto básico sobre la blancura: sabemos que el promedio para T1 es el más bajo y esto garantiza que los otros efectos serán positivos.
-
Aplicar una restricción al modelo ANOVA es necesario por razones teóricas, pero no tiene efecto en los resultados (ajuste, predicciones). La única diferencia radica en la forma en que se redactará el modelo.
-
En la pestaña Salidas (subpestaña Medias), marque una prueba de Tukey y una prueba REGWQ en el campo Comparaciones pareadas.
-
Active la opción Comparaciones con un control para realizar una prueba de Dunnett bilateral.
-
Haga clic en OK para iniciar los cálculos.
-
En el cuadro de diálogo de selección de la categoría de control, elija el grupo de control T1 para la prueba de Dunnett.
-
Una vez que haga clic en el botón OK, se reanudan los cálculos y se muestran los resultados.
Interpretación de un ANOVA unifactorial
Los primeros resultados mostrados por XLSTAT son los coeficientes de bondad de ajuste, incluidos el R² (coeficiente de determinación), el R² ajustado y varias otras estadísticas.
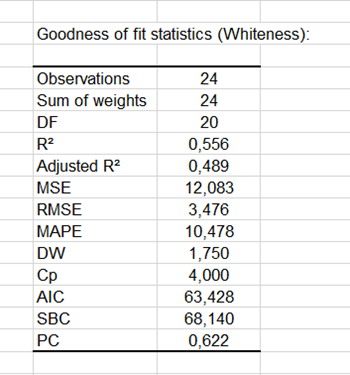
El coeficiente de determinación (aquí 0.56) proporciona una idea clara de cuánto de la variabilidad de la variable modelada (en este caso, la blancura) está siendo explicada por las variables explicativas (en este caso, el tipo de pasta de dientes); en nuestro caso, se explica el 56% de la variabilidad. El otro 44% está oculto en otras variables que no están disponibles y que el modelo oculta como "errores aleatorios".
La tabla de análisis de varianza es un resultado muy importante a considerar (ver abajo). Aquí es donde determinamos si la variable explicativa (la fórmula de la pasta de dientes) aporta información significativa (hipótesis nula H0) al modelo o no. En otras palabras, es una manera de preguntarse si es válido utilizar la media para describir toda la población, o si la información proporcionada por las categorías (en este caso, el tipo de pasta de dientes) tiene valor o no.
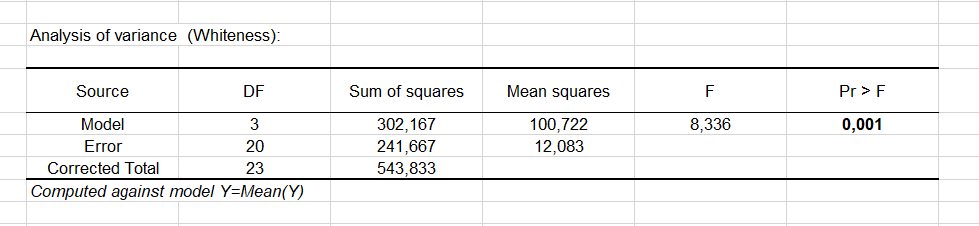
La prueba utilizada es la prueba del F de Fisher. Dado que la probabilidad asociada al F es, en este caso, de 0.001, significa que nos arriesgamos del 0.09% concluyendo que la variable explicativa origina una cantidad de información significativa al modelo.
El cuadro siguiente proporciona los detalles sobre el modelo y es esencial en cuanto que el modelo debe ser utilizado para proyectar previsiones o simulaciones. En nuestro caso particular no tiene mucho interés. Observaremos simplemente que el intervalo de confianza para el efecto del dentàfrico T2 incluye el valor 0, lo que indica que el dentàfrico T2 no es significativamente diferente de T1.
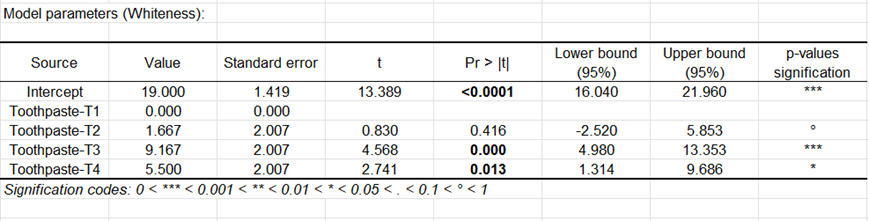
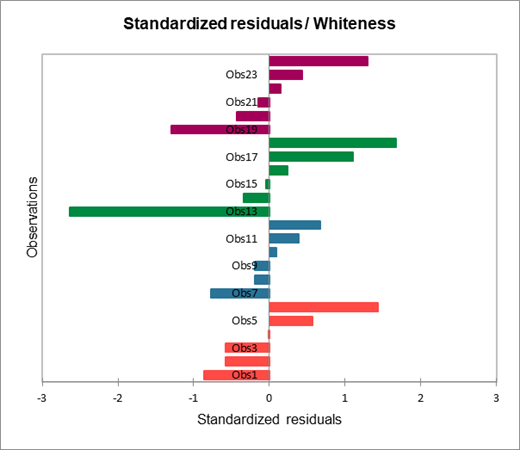
El gráfico de barras de los coeficientes estandarizados nos permite comparar visualmente el impacto relativo de las categorías y ver si los intervalos de confianza incluyen 0 o no.
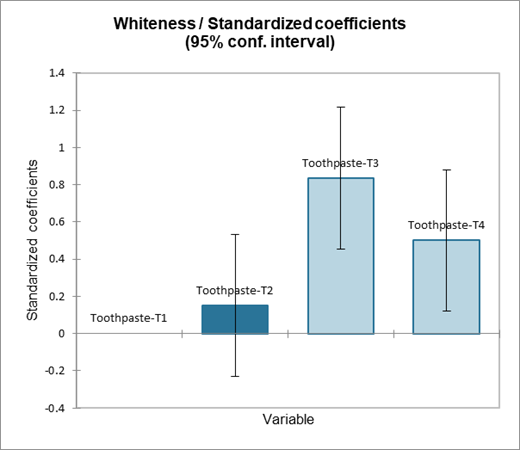
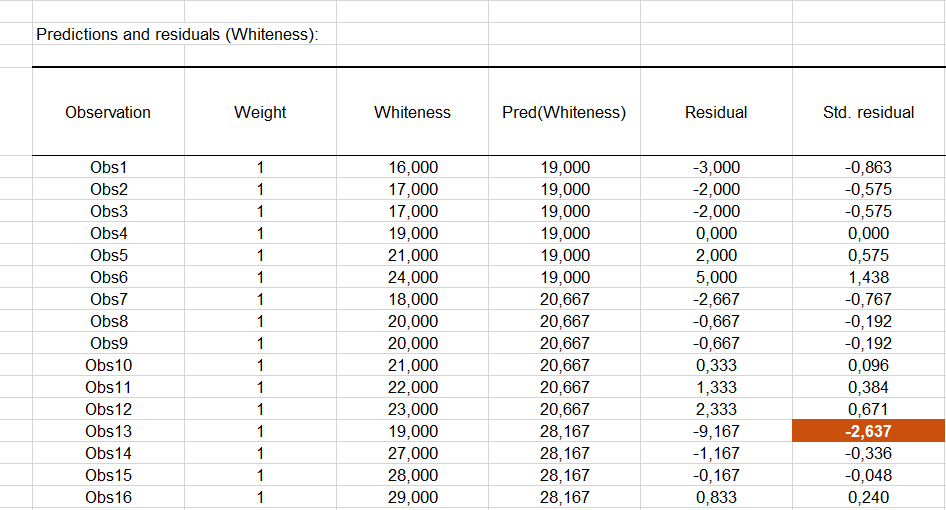
El cuadro siguiente expone el análisis de los residuos. Los residuos centrados reducidos deben tener una atención particular, dado que las hipótesis vinculadas al ANOVA, deben ser distribuidos según una ley normal N(0,1). Eso significa que el 95% de los residuos deben encontrarse en el intervalo [-1.96, 1.96]. Dado que el escaso número de datos del que disponemos aquà, cualquier valor fuera de este intervalo es revelador de un dato sospechoso. Podemos identificar aquà un valor sospechoso (decimotercera observación) el residuo siendo igual a -2.8279. Con el fin de explicar este valor, podremos verificar que el dentàfrico bueno fue entregado efectivamente a esa persona, o analizar la razón por la cual la reacción del paciente al dentàfrico fue más escasa que para otros.
El histograma de los residuos centrados reducidos permite señalar rápidamente la presencia de valores fuera del intervalo [-1.96, 1.96].
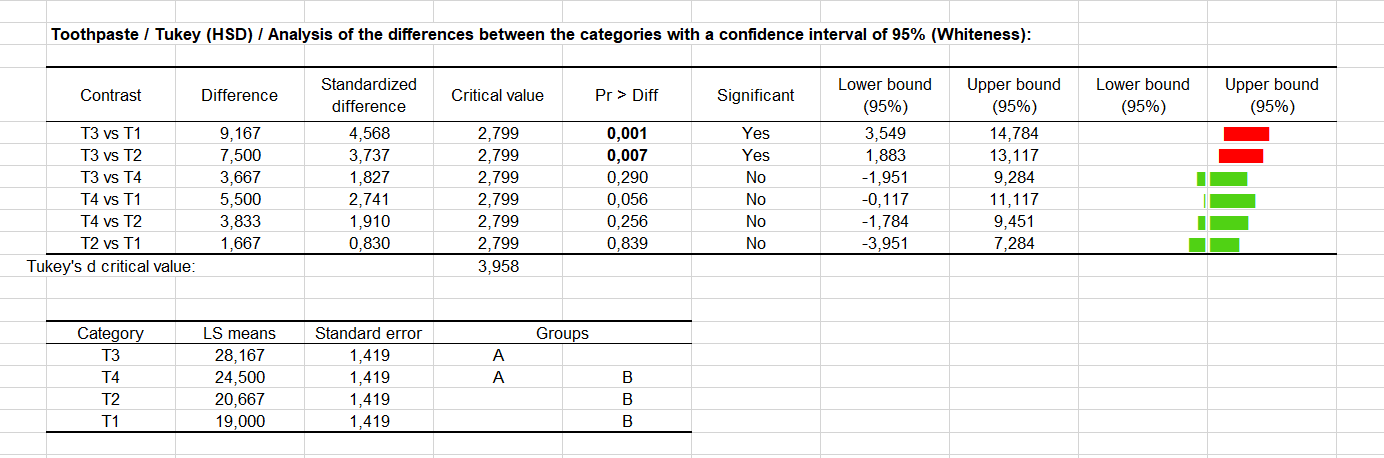
Por último, conseguiremos responder a nuestra pregunta inicial: ¿Existe una diferencia significativa entre los dentàfricos?, y en caso afirmativo, ¿Cómo podemos clasificarlos?. Como está mostrado en el cuadro a continuación, la prueba de Tukey HSD (Honestly Significantly Different), fue aplicada al conjunto de las parejas de diferencias posible. El riesgo de 5% que hemos elegido es utilizado para determinar el valor critico q, que es comparado a la diferencia entre las medias normalizadas. Otros programas se basan sobre el valor d, también proporcionado por XLSTAT. Solamente dos pares parecen ser significativamente diferentes (T1, T3) y (T2,T3). Utilizando el resultado de las pruebas, los dentàfricos son después clasificados. Apuntaremos que no hay transitividad ( significa no significativamente diferente, y significa significativamente diferente): T4 </> T3 T4 </> T2 but T2 <> T3
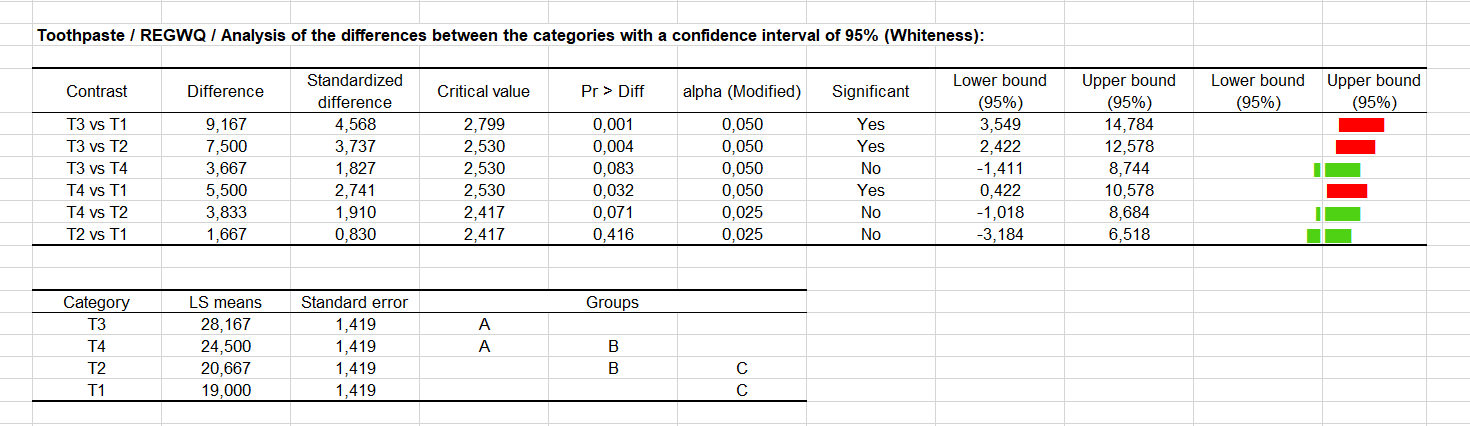
El procedimiento REQWQ proporciona un resultado diferente (ver más abajo), lo que demuestra que podemos ser prudente cuando utilizamos procedimientos de comparación múltiples.
Tres parejas de modalidades son aquà significativamente diferentes: T1 y T4 son aquà calificados significativamente diferentes. El cuadro de reagrupamientos destaca ahora tres grupos de modalidades.
La prueba de Dunnett fue calculado para comparar cada modalidad con la modalidad T1. La prueba de Dunnett destaca también una diferencia significativa entre T1 y T4.

Conclusión de este ANOVA unifactorial
En conclusión, los diferentes dentàfricos probados tienen un impacto significativamente diferente sobre la blancura de los dientes. Como el dentàfrico T1 ya está en el mercado, con el fin de promover el nuevo producto, los dentàfricos T3 o T4 podrán ser elegidos para ser puesto en el mercado.
Por favor, tenga en cuenta que ANOVA se fundamenta en una serie de asunciones paramétricas que deben ser verificadas para asegurarse de la fiabilidad del resultado.
¿Ha sido útil este artículo?
- Sí
- No