Modelo mixto de componentes aleatorios Excel

Este tutorial le mostrará cómo configurar e interpretar un modelo mixto de componentes aleatorios (random components mixed model) en Excel con el software XLSTAT.

Datos para ejecutar un modelo mixto de componentes aleatorios

Descargar los datos

Utilizamos un conjunto de datos procedentes de Mendenhall, Wackerly y Schaeffer (1996, Mathematical Statistics with Applications, Duxbury Press). En este ejemplo, se estudian lingotes hechos de diferentes metales. Buscamos conocer el impacto del lingote tratado y el tipo de metal que se utiliza como enlace en este lingote (N: níquel, I: hierro y C: cobre) sobre la presión necesaria para romperlo en dos. Tenemos 7 lingotes, tres tipos de uniones y una variable dependiente. Los lingotes tratados se han extraído de una población más grande y por lo tanto constituyen un factor aleatorio en nuestro modelo.

Un modelo lineal mixto se basa en el mismo modelo que un modelo lineal tradicional con un término asociado con los efectos aleatorios. El modelo tendrá la siguiente forma:

En nuestro caso, Y es la variable presión (press), X es la unión (factor fijo) y Z es el lingote (factor aleatorio). Por otra parte, podemos elegir la estructura de la matriz de covarianza de los efectos aleatorios. Vamos a elegir una estructura denominada “componente de la varianza”, que se basa en una matriz diagonal. Por favor, consulte la ayuda de XLSTAT para más detalles sobre la estructura de covarianza.

Configuración de un modelo mixto de componentes aleatorios

• Una vez abierto XLSTAT, seleccione el comando XLSTAT / Modelación de datos / Modelos mixtos, o bien haga clic en el botón correspondiente de la barra de herramientas Modelación de datos (véase más adelante).

• Una vez que haya hecho clic en el botón, aparece el cuadro de diálogo del modelo mixto.

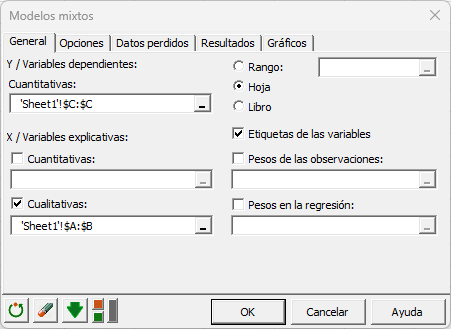
• Seleccione los datos en la hoja de cálculo de Excel.

• La Variable dependiente (o variable a modelar) es aquí la presión “pressure”.

• Nuestro objetivo es determinar el efecto de la unión y del lingote sobre la variabilidad de la presión.

• Puesto que hemos elegido el título de la columna para las variables, dejamos activada la opción Etiquetas de las variables.

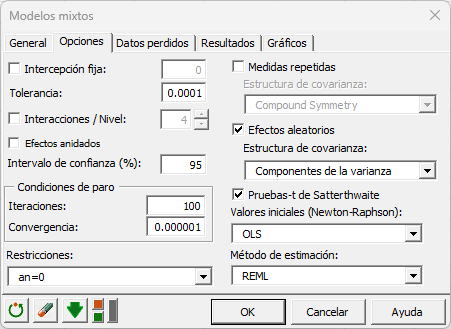
• Dejamos la opción de restricción en an=0, lo que significa que queremos que el modelo se construya bajo el supuesto de que el cobre tiene el efecto estándar en la presión.

• Cuando se trata de variables cualitativas, aunque es preciso aplicar una restricción al modelo de ANOVA por razones teóricas, ello no afectará a los resultados (bondad de ajuste). La única diferencia tiene que ver con la escritura real del modelo.

• La estructura de covarianza seleccionada es la pretedeterminada (i.e., componente de la varianza).

• Una vez que haya hecho clic en el botón OK, aparece un cuadro de diálogo para que pueda elegir qué factores han de ser tenidos en cuenta en el modelo. El efecto fijo es “metal” y el efecto aleatorio corresponde a los lingotes (“ingots”).

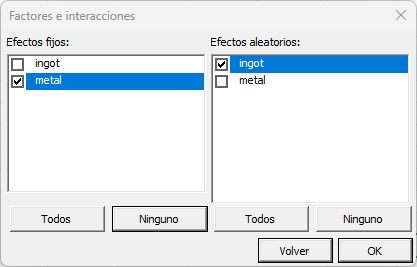
Nota: un factor no puede ser a la vez aleatorio y fijo.

• Una vez que haya hecho clic en el botón “OK”, se inician los cálculos. A continuación, se muestran los resultados.

Interpretación de los resultados de un modelo mixto de componentes aleatorios

Los primeros resultados que muestra XLSTAT son los coeficientes de bondad del ajuste.

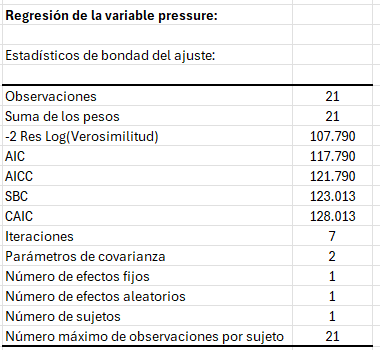
Los parámetros del modelo se obtienen utilizando el método de máxima verosimilitud restringida (REML), y serán diferentes a lo que sucede cuando se aplica un modelo lineal clásico. Todos los índices se utilizan para comparar modelos con diferentes estructuras de covarianza.
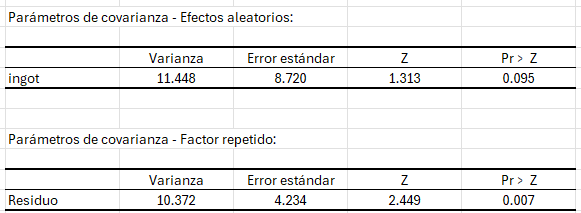
Se muestran a continuación las tablas de los parámetros de covarianza. La primera está asociada a los componentes aleatorios del modelo y la segunda está asociada a la matriz de covarianzas del error. En nuestro caso, ya que no hay medidas repetidas, la matriz de covarianzas del error es diagonal con un valor asociado a la varianza.

Se puede visualizar la matriz de covarianzas completa cuando se selecciona la matriz G (covarianza de componente aleatorio) y la matriz R (covarianza de error) en el cuadro de diálogo de salida.

Podemos ver que la varianza de error es significativa, y que el componente de variación aleatoria no es significativo. El componente aleatorio no tendrá un efecto significativo en el modelo global.

Para entender la influencia de los efectos fijos en el modelo, se estudian las pruebas de tipo III de efectos fijos. Podemos ver que el metal tiene un efecto significativo en el modelo.

El metal utilizado tiene un efecto significativo sobre la presión necesaria para romper el lingote.

Cuando nos fijamos en los parámetros del modelo (ver más abajo), podemos ver que el uso de hierro como unión del lingote produce un aumento significativo en la presión necesaria. El uso de níquel no produce una diferencia significativa.

Al mirar los coeficientes de efectos aleatorios, podemos ver que ningún coeficiente es significativo y, por lo tanto, llegamos a la conclusión de que el lingote tratado no tiene efecto en el modelo.

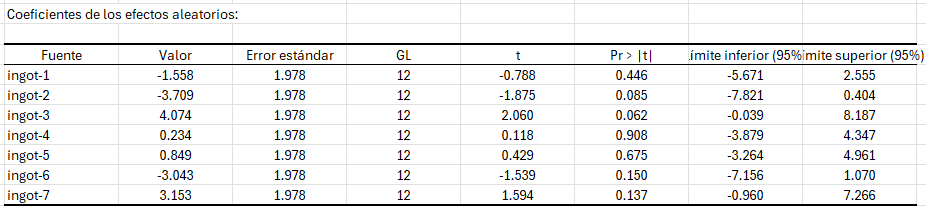
Por último, podemos decir que la unión es el único factor en el modelo que tiene un efecto significativo sobre la presión necesaria para romper el lingote.
En XLSTAT están disponibles algunos otros resultados tales como residuos, gráficos de los residuos, etc.