Modèle mixte avec facteur aléatoire dans Excel

Jeu de données pour appliquer un modèle à facteurs aléatoires en utilisant les modèles mixtes

Nous étudions des données utilisées dans Mendenhall, Wackerly et Schaeffer (1996, Mathematical Statistics with Applications, Duxbury Press). Dans cet exemple, des lingots composés de différents métaux sont étudiés.

Nous cherchons à connaître l’impact du lingot traité et du type de métal servant de lien dans ce lingot (n : nickel, i : fer et c : cuivre) sur la pression requise pour casser en deux ce lingot. Nous avons donc 7 lingots différents, trois types de liens et une variable dépendante quantitative (la pression). Les lingots traités sont tirés aléatoirement et constituent donc un effet aléatoire dans notre modèle.

Un modèle linéaire mixte est basé sur le même modèle qu’un modèle linéaire classique avec un terme associé aux effets aléatoires. Le modèle aura la forme suivante :

Dans notre cas, Y est la variable pression, X correspond aux effets fixes (ici le métal utilisé) et Z contient les effets aléatoires (le lingot analysé). De plus, nous pouvons choisir la structure de la matrice de covariance entre les effets aléatoires cov(gamma).

Nous choisirons une structure classique appelée « variance component » qui est basé sur une matrice de covariance diagonale. Pour obtenir des détails sur les structures de covariance, veuillez consulter l’aide d’XLSTAT.

Paramétrer un modèle à facteurs aléatoires en utilisant les modèles mixtes

• Une fois XLSTAT lancé, choisissez la commande XLSTAT / Modélisation / Modèles mixtes ou cliquez sur le bouton Modèles mixtes de la barre d'outils Modélisation.

• Une fois le bouton cliqué, la boîte de dialogue correspondant aux modèles mixtes apparaît. Dans le premier onglet, vous pouvez sélectionner les données sur la feuille Excel.

• La Variable dépendante correspond à la variable expliquée (ou variable à modéliser), qui est dans ce cas précis pression.

• Toutes les variables restantes sont qualitatives, sélectionnez les deux variables (vous devez sélectionner aussi bien les variables associées aux effets fixes que celles associées aux effets aléatoires).

• L'option Libellés des variables est laissée activée car la première ligne des colonnes comprend le nom des variables.

• Dans l'onglet Options, il n’y a pas de mesures répétées dans notre modèle donc l’option mesures répétées n’est pas activée (la matrice de covariance des erreurs sera donc diagonale avec la valeur de la variance sur la diagonale).

• L’option facteur aléatoire doit être activée et nous sélectionnons comme structure variance component.

• Nous choisissons la contrainte an=0, ce qui implique que le modèle s'écrira de façon à considérer que le cuivre aura l'effet de base.

• Appliquer une contrainte lorsqu’on a des facteurs qualitatifs est indispensable pour des raisons théoriques, mais cela ne change ni les résultats, ni la qualité de l'analyse.

• Une fois que l'utilisateur a cliqué sur OK, une nouvelle fenêtre permettant de sélectionner les facteurs fixes et les facteurs aléatoires apparaît :

• Nous appliquons un modèle mixte en utilisant comme effet fixe la variable "métal" et comme effet aléatoire la variable "lingot".

• Une fois que l'utilisateur a cliqué sur OK, les calculs reprennent et les résultats sont affichés.

Interpréter les résultats d'un modèle à facteurs aléatoires en utilisant les modèles mixtes

Le premier tableau de résultats fournit les coefficients d'ajustement et des informations associées aux données.

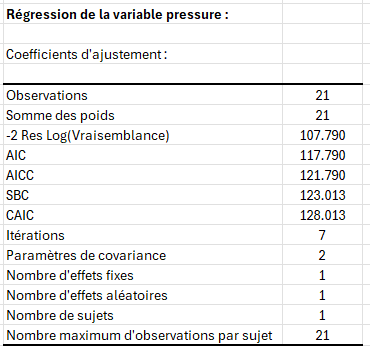
Les coefficients du modèle sont obtenus en utilisant le maximum de vraisemblance restreint (REML), on obtient donc des indices différents de ceux du modèle linéaire classique. Les AIC, AICC, SBC et CAIC sont des indices qui permettent de comparer des modèles en utilisant différentes structures de matrices de covariance.

Les deux tableaux suivants donnent les paramètres des matrices de covariance du modèle. Tout d’abord, les covariances associées aux effets aléatoires (paramètres de covariance — facteurs aléatoires), puis celles associées au terme d’erreur du modèle (Paramètre de covariance — mesures répétées). XLSTAT permet d’afficher aussi les matrices complètes de covariance et de corrélation induites par le modèle (la matrice associée aux composantes aléatoires est appelée matrice G). Dans notre cas, les deux matrices sont diagonales. Pour la covariance des erreurs, la variance obtenue est significative alors que pour les effets aléatoire, la variance n'est pas significative. Ceci nous montre qu'on risque d'avoir un effet aléatoire non significatif.

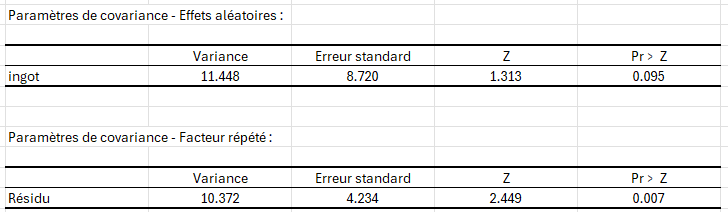
Nous voulons maintenant savoir si les effets fixes contribuent à expliquer la variable dépendante. Pour cela nous devons analyser les tableaux de résultats des tests de type III des effets fixes.

Le tableau des tests de type III des effets fixes permet de vérifier la significativité des effets fixes en utilisant un test F de Fisher. Nous voyons donc que le type de matériaux utilisé a un effet sur la pression nécessaire. Le tableau suivant rassemble les paramètres du modèle, leur écart-type ainsi qu’un intervalle de confiance. Ces paramètres s’interprètent de la même façon que dans le cas d’un modèle linéaire classique.

L’analyse de la composante aléatoire peut être faite en utilisant le tableau des effets aléatoires.

Nous voyons que le lingot sélectionné n’a pas d’impact significatif sur la pression nécessaire. Ainsi, le choix du lingot n’aura pas d’impact sur le modèle. C’est uniquement le liant qui aura un impact sur la pression nécessaire.

Cette analyse nous a permis d’analyser un modèle mixte en prenant en compte l’aspect aléatoire de certains effets.
D’autres sorties sont disponibles dans XLSTAT et nous permettrons d’approfondir notre analyse. Par exemple, les différents types de résidus ainsi que les graphiques associés aux résidus.