Analyse de contrastes à l'issue d'une ANOVA à un facteur dans Excel
Ce tutoriel explique comment calculer et interpréter une analyse de contrastes à l'issue d'une ANOVA avec Excel en utilisant XLSTAT
Jeu de données pour l'analyse de contrastes à l’issue d’une ANOVA à un facteur
Le jeu de données correspond à une expérimentation en agronomie visant à tester l’effet de 4 traitements (contrôle, engrais K, engrais N et engrais P) sur un rendement de maïs. Chaque traitement est appliqué sur huit parcelles distinctes.
But de ce tutoriel sur l’analyse de contrastes à l’issue d’une ANOVA à un facteur
Ce tutoriel a pour objectif de se focaliser sur des questions très précises qu’on peut se poser à l’issue d’un modèle linéaire (ici une ANOVA à un facteur). Par exemple, nous pouvons nous demander si un engrais est capable de doubler (ou tripler) significativement le rendement agricole. Nous pouvons aussi nous demander si la différence entre deux ensembles de moyennes distincts est significative, par exemple, si trois engrais améliorent significativement en moyenne le rendement par rapport au contrôle. Il est possible de répondre à ces questions à travers la manipulation de contrastes. Techniquement, un contraste correspond à une somme pondérée des coefficients d’un modèle linéaire. La différence entre cette somme et zéro est testée.
Quelques notes préliminaires
Avant d’illustrer le concept de contrastes et d’en paramétrer, il est vivement recommandé d’extraire les noms des coefficients du modèle étudié (ici ANOVA à un facteur) tels qu’ils sont définis par XLSTAT. Ces noms peuvent facilement être récupérés dans les résultats d’ANOVA à un facteur fournis par XLSTAT. Cliquer sur modélisation / ANOVA, et procéder au paramétrage en suivant ce tutoriel par exemple. Détails du paramétrage : variable dépendante = rendement ; variable explicative qualitative = engrais.
Dans les résultats, examiner le tableau intitulé « paramètres du modèle »

La colonne Source contient les noms donnés par XLSTAT aux coefficients du modèle, et Valeur les valeurs de ces coefficients qui structurent l’équation du modèle liant la variable explicative (facteur « engrais ») à la variable à expliquer (rendement) affichée en-dessous. XLSTAT utilise par défaut la moyenne de la première modalité (par ordre alphanumérique) du facteur étudié (ici la modalité « Contrôle ») en guise de modalité de référence (Intercept) pour le calcul des effets. L’effet des autres modalités est calculé sous forme de différence de la moyenne de la modalité avec la moyenne de référence. Par exemple, la différence de moyenne entre la modalité P et la modalité Contrôle est de 26.90. Cet écart est significativement différent de zéro (P value < 0.0001). Cela indique une différence significative entre la modalité Contrôle et la modalité P.
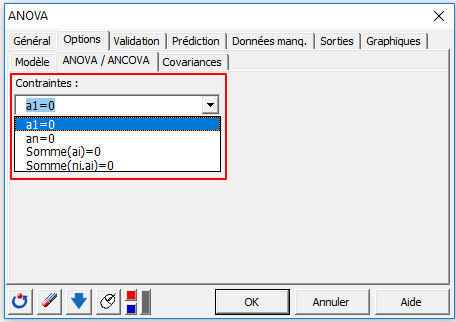
Notez que le mode calcul des effets peut être modifié pendant le paramétrage de l’ANOVA dans l’onglet options / contraintes. Une contrainte an=0 utilisera la dernière modalité (modalité P) en modalité de référence. Une contrainte somme(ai)=0 examinera les écarts de toutes les modalités par rapport à la moyenne générale des données. Une contrainte somme(ni.ai)=0 (utilisée moins souvent) permet en plus de prendre en compte la taille des groupes dans la définition de la contrainte.
Contrastes, approche conceptuelle
Conceptuellement, tester si une valeur de coefficient (colonne Valeur) est différente de zéro revient à annuler tous les autres coefficients dans l’équation du modèle et de comparer le résultat à zéro.
Par exemple, pour le coefficient engraisN (écart par rapport à la modalité de référence), l’équation s’écrit :
0 x Constante + 0 x engraisC + 0 x engraisK + 1 x engraisN + 0 x engraisP (1)
= engraisN
= 67.038
L’écart entre la valeur 67.038 et zéro est testée (ici cet écart est significatif : P value < 0.0001).
Reprenons l’équation (1) et multiplions le coefficient engraisN par 1 :
0 x Constante + 0 x engraisC + 0 x engraisK + 1 x engraisN + 0 x engraisP
L’ensemble des chiffres multipliant chaque coefficient du modèle dans un test particulier constitue un contraste. Ici nous appelons arbitrairement le contraste Cont1, que nous écrivons de la sorte :
Cont1 : 0 0 0 1 0
Ainsi, le contraste correspondant au test du coefficient engraisP s’écrit :
Cont2 : 0 0 0 0 1
Nous pouvons définir un contraste pour tester si la moyenne du rendement des parcelles soumises à l’engrais K est significativement différente de zéro. Ceci revient à faire la somme entre la modalité de référence (Constante) et l’écart ajouté par l’engrais K (coefficient engraisK) et de tester si cette somme est significativement différente de zéro. Le contraste s’écrit de la sorte :
Cont3 : 1 0 1 0 0
Nous pouvons nous demander si l’apport de l’engrais N est au moins deux fois plus important que l’apport de l’engrais P. Cela revient à voir si la différence entre engrais-N – 2 x engrais-K est positive et significative. Ceci peut se paramétrer sous forme de contraste :
Cont4 : 0 0 0 1 -2
Par ailleurs, nous pouvons nous intéresser à l’apport moyen des trois engrais (K, N, P) par rapport au contrôle. Cela revient à calculer l’écart entre la moyenne des apports des engrais et zéro et te tester sa significativité. Mathématiquement, cette moyenne s’écrit de la sorte :
(engraisK + engraisN + engraisP)/3 = 0.33 x engraisK + 0.33 x engraisN + 0.33 x engraisP
Le contraste équivalent :
Cont5 : 0 0 0.33 0.33 0.33
Enfin, nous nous demandons si l’engrais N double (au moins) le rendement agricole total du contrôle. Nous pouvons répondre à cette question en vérifiant si la quantité moyenne(parcelles N) – 2 x moyenne(parcelles Contrôle) est positive et significativement différente de zéro. Traduisons équation en utilisant les coefficients avant d’écrire le contraste équivalent :
moyenne(parcelles N) – 2 x moyenne(parcelles Contrôle)
= Constante + engraisN – 2 x (Constante + engraisContrôle)
= engraisN – Constante
Contraste :
Cont6 : -1 0 0 1 0
Analyse de contrastes, pratique avec XLSTAT
Dans les résultats de l’ANOVA, copier la colonne contenant les noms des coefficients et la coller dans la page des données (2 figures). Cette étape n’est pas obligatoire mais elle facilite la définition des contrastes souhaités.
Ecrire les contrastes souhaités en colonnes en face des coefficients (une colonne par contraste). Ici nous prendrons les 6 contrastes définis dans le paragraphe précédent.
Pour une meilleure lisibilité, inclure les noms de contrastes au-dessus de chaque colonne.
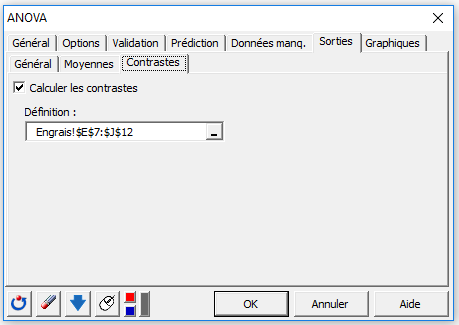
Paramétrer la même ANOVA de nouveau, en rajoutant une option : dans Sorties / Contrastes, cocher la case Calculer les Contrastes et sélectionner la matrice de contrastes (incluant les noms de colonnes, mais excluant la colonne des coefficients) (figure). Cliquer sur OK.
L’analyse de contrastes apparaît à la fin des résultats ANOVA.

Chaque contraste est défini par une valeur correspondant à la quantité testée et calculée dans l’équation du contraste, associée à une erreur standard et aux bornes inférieure et supérieure d’un intervalle de confiance à 95%. Enfin, une statistique t et une P value associée permettent de voir si la valeur calculée est significativement différente de zéro.
Voici un récapitulatif des questions posées dans le paragraphe précédent et leur résolution via l’analyse de contrastes :
Cont1 : L’écart entre N et le contrôle est-il significatif au seuil 0.05?
Réponse : Oui (P value < 0.0001)
Cont2 : L’écart entre P et le contrôle est-il significatif au seuil 0.05 ?
Réponse : Oui (P value < 0.0001)
Cont3 : Quelle est la moyenne du rendement des parcelles soumises à l’engrais K. Cette moyenne est-elle significativement différente de zéro au seuil 0.05?
Réponse : moyenne = 73.938, significativement différente de zéro (P value < 0.0001)
Cont4 : l’apport de l’engrais N est au moins deux fois plus important que l’apport de l’engrais P au seuil 0.05 ?
Réponse : Oui, car la valeur du contraste est positive (+13.238) et significative (P value < 0.05).
Cont5 : Quel est l’apport moyen des trois engrais (K, N, P) par rapport au contrôle, et cet apport est-il significatif au seuil 0.05?
Réponse : apport = 30.958, significativement différent de zéro (P value < 0.0001)
Cont6 : L’engrais N double-t-il (au moins) le rendement agricole total du contrôle au seuil 0.05?
Réponse : la différence entre le rendement des parcelles soumises à l’engrais N et le double de celui des parcelles contrôle n’est pas significative au seuil choisi (P value > 0.05).
Pour aller plus loin
Les contrastes peuvent être définis quelle que soit la complexité du modèle linéaire mis en jeu (ANOVA à plusieurs facteurs avec interactions, ANCOVA, etc.). Ainsi, dans les modèles impliquant des variables explicatives quantitatives, il sera possible de manipuler des coefficients correspondant à des pentes ou à des différences de pentes.
Cet article vous a t-il été utile ?
- Oui
- Non