Prueba de Kruskal-Wallis: tutorial en Excel

Este tutorial le mostrará cómo configurar e interpretar una Prueba de Kruskal-Wallis sobre dos muestras independientes en Excel usando XLSTAT.

¿No está seguro de si esta es la prueba estadística que está buscando? Consulte por favor esta guía.

Datos para ejecutar una prueba de Kruskal-Wallis en Excel usando XLSTAT

Los datos corresponden a un análisis sensorial, donde se ha pedido a 10 expertos que califiquen a ciegas durante dos sesiones separadas la dureza de cuatro tipos de quesos, en una escala [0-> 5]. En el tutorial sobre el test de Friedman se consideró que los mismos 10 expertos calificaron a los cuatro quesos (los datos fueron emparejados debido a eso). Aquí, consideramos que diferentes expertos calificaron los quesos. Nuestro objetivo es determinar si la diferencia de dureza entre los quesos es significativa o no.

Configuración de una prueba de Kruskal-Wallis en XLSTAT

Una vez activado XLSTAT, seleccione el comando XLSTAT / Pruebas no paramétricas / Comparación de k muestras, o bien haga clic en el botón correspondiente del menú Pruebas no paramétricas (véase más abajo).

Una vez que haya hecho clic en el botón, aparece el cuadro de diálogo. Active en primer lugar la opción Una columna por muestra y, a continuación, haga clic en el campo Muestras, y seleccione los datos en la hoja de Excel: seleccione con el ratón las 4 columnas de datos correspondientes a los 4 quesos (o muestras, o tratamientos).

Ya que los nombres de los quesos se incluyen en la primera fila de la selección, deje marcada la opción Etiquetas de las columnas.

A continuación, active la opción Comparaciones múltiples y la opción Bonferroni, de modo que si la hipótesis de que los quesos son los mismos es rechazada, se puede identificar quesos son diferentes.

Tras hacer clic en el botón OK, aparecen los resultados en una nueva hoja de Excel (ya que esa es la opción seleccionada para los resultados).

Interpretación de una prueba de Kruskal-Wallis

La primera tabla muestra el estadístico K de Kruskal-Wallis y el valor p correspondiente. El valor de p nos dice que la probabilidad de rechazar la hipótesis nula aunque sea verdadera es aproximadamente 0.0005. Concluimos que podemos rechazar firmemente la hipótesis nula de que no hay diferencia entre los quesos.

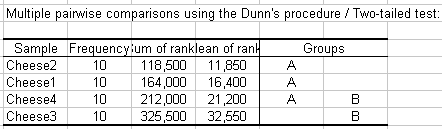
Los siguientes resultados permiten identificar qué quesos son diferentes de los demás, como se haría con pruebas de comparaciones múltiples en ANOVA. Para tener en cuenta el hecho de que hay múltiples comparaciones sobre los k grupos, se utiliza la corrección de Bonferroni. A partir de la tabla de abajo podemos ver que los quesos 2 y 3, y 1 y 3 se identifican como diferentes. Mirando hacia atrás en los datos, el queso número 3 es claramente el queso más duro.