Prueba F de Fisher para comparar dos varianzas en Excel
Este tutorial le mostrará cómo someter a prueba la diferencia entre dos varianzas observadas, mediante la prueba de Fisher, en Excel usando el software XLSTAT.
¿No está seguro si esta es la prueba estadística que está buscando? Consulte por favor esta guía.
Datos para ejecutar una prueba F de Fisher en XLSTAT para evaluar lal igualdad de la varianza de 2 muestras
Los datos provienen de [Fisher M. (1936). The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7, 179 -188], y se corresponden con las características de los sépalos de las flores 100 iris descritas por dos variables (longitud del sépalo, anchura del sépalo). Hay dos especies diferentes incluidas en este ejemplo: setosa y versicolor.
Objetivo de este tutorial
Nuestro objetivo es evaluar si hay una diferencia entre las especies en la longitud y la anchura de los sépalos. A continuación, compararemos la distribución de estas variables para las 2 muestras.
Comprobación de la normalidad de las muestras
Lo primero que debemos hacer es evaluar si las muestras siguen una distribución normal, dado que la preba F de Fisher es sensible a los datos que no siguen una distribución normal. Encontrará esos estadísticos calculados en la hoja de cálculo de Excel. Todas las 4 muestras (Versicolor-longitud sépalo, Versicolor-anchura sépalo, Setosa- longitud sépalo, Setosa- anchura sépalo) siguen una distribución normal.
Configuración de una prueba F de Fisher en XLSTAT para evaluar lal igualdad de la varianza de 2 muestras
A continuación, hacemos una prueba de F para saber si las varianzas son iguales. Si las varianzas son iguales, podemos hacer una prueba para comparar los promedios. Para llevar a cabo una comparación de las varianzas de dos muestras, seleccionamos en el menú Pruebas paramétricas / Comparación de las varianzas de dos muestras.
 En el cuadro de diálogo de la comparación de las varianzas dos muestras, en la pestaña General, seleccione los datos de las muestras 1 y 2. Para la Muestra 1 seleccione la columna B (que contiene la longitud sépalo de la variedad Versicolor), y para la Muestra 2 la columna E (correspondiente a la longitud sépalo para la muestra Setosa).
En el cuadro de diálogo de la comparación de las varianzas dos muestras, en la pestaña General, seleccione los datos de las muestras 1 y 2. Para la Muestra 1 seleccione la columna B (que contiene la longitud sépalo de la variedad Versicolor), y para la Muestra 2 la columna E (correspondiente a la longitud sépalo para la muestra Setosa).
El Formato de datos es Una columna por muestra, dado que cada columna corresponde a una de las muestras.
Seleccionamos la opción de Hoja para obtener los resultados en una nueva hoja de cálculo del libro.
Puesto que las columnas tienen etiquetas, dejamos seleccionada la opción Etiquetas de las columnas.
La prueba que decidimos realizar es la Prueba F de Fisher.

Una vez fijadas todas estas elecciones, podemos pasar a la pestaña Opciones.
Queremos someter a prueba la igualdad de varianzas, lo que significa que necesitamos poner a prueba la hipótesis alternativa: Varianza 1 / Varianza 2 ≠ R, donde R es 1.
Mantenemos el nivel de significación del 5% establecido por defecto.
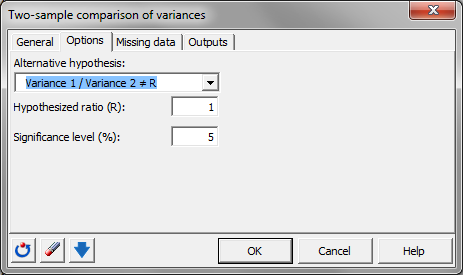
No tenemos datos perdidos, de modo que podemos ir directamente a la pestaña Resultados y marcamos la única opción disponible: Estadísticos descriptivos.

Pulse OK, cuando todo esté listo.
Resultados de una prueba F de Fisher en XLSTAT para evaluar lal igualdad de la varianza de 2 muestras
Los resultados que aparecen en una nueva hoja muestran que la hipótesis H0 debe ser rechazada, dado que el valor de p de 0.009 es inferior a nuestro límite del 5%. Por tanto, las varianzas no pueden ser considerados iguales. La longitud de los sépalos en las dos poblaciones -Versicolor y Setosa- no siguen la misma distribución.
Ahora vamos a hacer lo mismo pero para la anchura de los sépalos.
El único cambio en el procedimiento descrito anteriormente es la selección de datos. Para la Muestra 1 seleccionamos la columna C y para la Muestra 2 seleccionamos la columna F.

En esta ocasión las varianzas pueden ser consideradas como iguales, ya que el valor p de la prueba (0.189) es superior a 0.05.

Puesto que asumimos que existe igualdad de varianzas u homocedasticidad, podemos realizar una prueba de comparación de las medias.
Podemos notar en la Tabla de estadística descriptiva que la media de la anchura del sépalo para Versicolor es inferior a la media de Setosa para la misma característica. En consecuencia, podemos ejecutar una prueba de una cola para la prueba de la media.
Seleccionamos en el menú Pruebas paramétricas / Pruebas t y z para dos muestras

En la pestaña General hacemos la misma selección de la muestra que anteriormente hicimos para la anchura del sépalo.
Seleccionamos la opción de Prueba de Student, ya que no conocemos las varianzas verdaderas de las poblaciones.

En la pestaña Opciones elegimos la alternativa Media 1 – Media 2 < D, donde D es 0.
Podemos Suponer la igualdad de las varianzas, ya que antes hemos calculado la prueba correspondiente.

Hacemos clic en OK.
Como puede verse en los resultados de esta prueba, se concluye que hay diferencia significativa entre las dos medias, de manera que la anchura de sépalo de la iris Versicolor es menor que la anchura del sépalo de la iris Setosa. La variable anchura de los sépalos en las dos poblaciones -Versicolor y Setosa- no siguen la misma distribución.

¿Ha sido útil este artículo?
- Sí
- No