Comparar ≥ 2 muestras descritas por varias variables

Este tutorial le mostrará cómo comparar las muestras descritas por varias variables utilizando la distancia de Mahalanobis en Excel con el software XLSTAT.

Datos para probar la diferencia entre muestras utilizando la distancia de Mahalanobis

Comprobación de la diferencia entre las muestras utilizando la distancia de Mahalanobis

Con el fin de demostrar cómo utilizar la herramienta y la pertinencia de las pruebas, haremos en primer lugar una prueba multidimensional sobre las 3 primeras columnas, luego sobre las 3 siguientes, y por último sobre las 6 columnas conjuntamente.

1. Pruebas sobre las tres primeras columnas

Configuración de una prueba multidimensional Una vez activado XLSTAT, seleccione el comando XLSTAT / Pruebas paramétricas / Pruebas multidimensionales, o bien haga clic en el botón correspondiente de la barra de herramientas Pruebas paramétricas (véase siguiente captura de pantalla).

Al hacer clic en el botón, aparece un cuadro de diálogo. Seleccione los datos correspondientes a las tres primeras columnas en la hoja de Excel y, a continuación, seleccionamos la columna B que contiene los identificadores de grupo.

Haga clic en OK para iniciar los cálculos.

Resultados de la prueba multidimensional

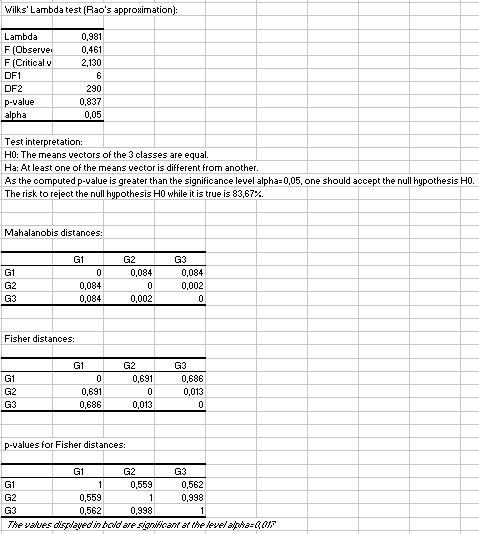
Los resultados indican que tanto para las medias (prueba de Wilks) como para las matrices de covarianzas (pruebas de Box y Kullback), los tres grupos se pueden considerar como idénticos y extraidos de la misma población. Observamos con distancias de Fisher que la distancia entre G1, por un lado, y G2 o G3 por otro lado, es mayor que la distancia entre G2 y G3, pero esa diferencia no llega a ser significativa.

2. Pruebas sobre las últimas tres columnas

Esta vez elegimos sólo las últimas tres columnas. El resto de las opciones permanecen sin cambios.

En este caso, las pruebas sobre las medias identifican la diferencia: la prueba Lambda de Wilks llega a la conclusión de que existe una diferencia significativa entre las medias de los grupos. Nos damos cuenta de que las distancias de Mahalanobis sólo son significativas cuando se refieren al grupo 3. No es de extrañar que la pequeña diferencia entre los 2 primeros grupos no se haya detectado como significativa, ya que el tamaño del grupo es demasiado reducido como para identificar una diferencia tan pequeña.

En lo que atañe a las matrices de covarianza, las pruebas de Box están en el límite para encontrar una diferencia, obteniendo un valor de p de 0.06. Pero la prueba de Kullback no logra identificar la diferencia. Esto es debido que los tamaños de los grupos son demasiado pequeños para distinguir grupos en los cuales las varianzas son 5’² y 7’².

3. Pruebas sobre las seis columnas

Esta vez seleccionamos todas las columnas. En la pestaña “Resultados” solicitamos las matrices de correlaciones y de covarianzas.

Las pruebas sobre las medias rinden resultados muy similares al caso 2 (véase más arriba). La diferencia entre G1 y G2 basada en la distancia de Mahalanobis es ligeramente inferior.

Sin embargo, las pruebas sobre las matrices de covarianza son sorprendentemente diferentes. Se acumulan las pequeñas diferencias observadas en las 3 primeras columnas, y las más grandes observadas en las últimas 3 columnas. Además hay covarianzas no despreciables entre RV1 y RV4, entre RV2 y RV5 y entre RV3 y RV6. Al final, esto arroja diferencias significativas cuando las pruebas se realizan sobre las 6 columnas.