Compare ≥ 2 samples described by several variables

This tutorial will help you compare samples described by several variables using the Mahalanobis distance in Excel with the XLSTAT software.

Dataset to test the difference between samples using the Mahalanobis distance

This tutorial is based on artificial data that have been generated with the distribution sampling tool of XLSTAT. The first three columns are drawn in a standard normal distribution N(0,1). The following three columns have been sampled in a Normal N(2, 5) distribution for G1, in a Normal N(2.2, 5.2) distribution for G2 and in a Normal N(8, 7) distribution for G3.

Testing the difference between samples using the Mahalanobis distance

In order to demonstrate how to use the tool and the relevance of the tests, we will first do a multidimensional test on the first 3 columns, and then on the following 3, and then on the 6 columns together.

1. Tests on the first three columns

Setting up a multidimensional test

Once XLSTAT is activated, select the XLSTAT / Parametric tests / Multidimensional tests command, or click on the corresponding button of the Parametric tests toolbar (see below).

When you click on the button, a dialog box appears. Select the data corresponding to the first three columns on the Excel sheet, then select column B that contains the group identifiers.

Click OK to launch the computations.

Results of the multidimensional test

The results indicate that for both averages (Wilks test) and covariance matrices (Box and Kullback tests), the three groups can be regarded as identical and from the same population. We note with the Fisher's distances that the distance between G1, on the one hand, and G2 or G3 on the other hand, is greater than the distance between G2 and G3, but still not significant however.

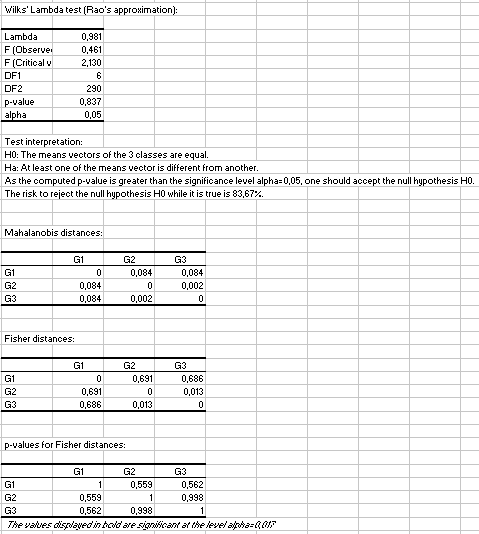
2. Tests on the last three columns

This time we select only the last three columns. Other options are unchanged.

In this case, tests on averages identify the difference: the test of the Wilks' Lambda concludes that there is a significant difference between the groups means. We notice that the Mahalanobis distances are only meaningful when the group 3 is concerned. It is not surprising that the small difference between the first 2 groups has not been detected as significant, as the group size is too small to identify such a small difference.

Regarding the covariance matrices, the Box tests are on the borderline of finding a difference, the p-value being equal to 0.06. But the test of Kullback fails to identify the difference. This is due to the size of the groups that are too small to distinguish groups for which variances are 5’² and 7’².

3. Tests on the six columns

This time all columns are selected. In the "Outputs" tab we request correlation and covariance matrices.

Tests on the means yield results very close to the case 2 (see above). The difference between G1 and G2 based on the Mahalanobis distance is slightly lower.

However, the tests on the covariance matrices are surprisingly different. Small differences observed on the first 3 columns, and the larger ones observed on the last 3 columns accumulate. Furthermore there are non neglectable covariances between RV1 and RV4, between RV2 and RV5 and between RV3 and RV6. In the end this gives significant differences when the tests are performed on the 6 columns.