Vergleich von ≥ 2 Stichproben die durch mehrere Variablen beschrieben sind

Dieses Tutorium wird Ihnen helfen, Stichproben, die durch mehrere Variablen beschrieben sind, mithilfe des Mahalanobis-Abstands in Excel mit der XLSTAT Software zu vergleichen.

Datensatz für das Testen der Differenz zwischen Stichproben mithilfe des Mahalanobis-Abstands

Um die Benutzung dieses Tool besser zu verstehen und die Relevanz der Tests zu betrachten, wird zunächst ein multidimensionaler Test auf den ersten 3 Spalten und dann auf den folgenden 3 Spalten und schließlich auf den gesamten 6 Spalten zusammen durchgeführt.

1. Tests auf den ersten drei Spalten

Einrichten eines multidimensionalen Tests

Nach dem Aktivieren von XLSTAT-Pro wählen Sie den Befehl XLSTAT/Parametrische Tests/Multidimensionale Tests oder klicken Sie auf den entsprechenden Button der Symbolleiste Parametrische Tests (siehe unten).

Nach dem Klicken auf den Button erscheint ein Dialogfenster. Wählen Sie die den ersten drei Spalten entsprechenden entsprechenden Daten auf den Excelblatt aus, dann die wählen Sie die Spalte B, die den Gruppenidentifikator enthält.

Klicken Sie auf OK, um die Berechnungen zu beginnen.

Ergebnisse des multidimensionalen Tests

Die Ergebnisse zeigen an, dass für beide Durchschnitte (Wilks' Test) und Kovarianzmatrizen (Box- und Kullback-Tests) die drei Gruppen als identisch und aus derselben Population angesehen werden können. Wir stellen bei den Fisher-Distanzen fest, dass die Distanz zwischen G1 einerseits und G2 oder G3 andererseits größer ist als die Distanz zwischen G2 und G3, jedoch immer noch nicht signifikant.

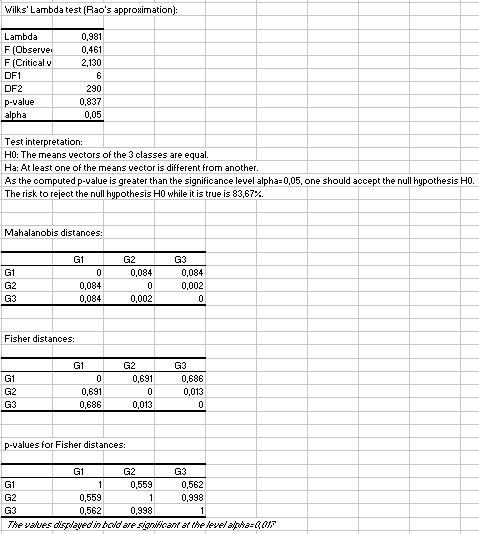
2. Test auf

2. Tests auf den letzten drei Spalten

Dieses Mal wählen wir nur die letzten drei Spalten aus. Andere Optionen bleiben unverändert.

In diesem Fall decken die Tests der Mittelwerte den Unterschied auf: Wilks' Lambda-Test lässt den Schluss zu, dass eine signifikante Differenz zwischen den Gruppenmittelwerten besteht. Wir stellen fest, dass die Mahalanobis-Abstände nur von Bedeutung sind, wenn die Gruppe 3 betroffen ist. Es ist nicht überraschend, dass die kleine Differenz zwischen den ersten beiden Gruppen nicht als signifikant erkannt wurde, da die Gruppengröße zu klein ist, um eine solche kleine Differenz zu identifizieren.

Betrachtet man die Kovarianzmatrizen, so sind die Box-Tests im Begriff fast einen Unterschied anzuzeigen, der p-Wert liegt bei 0,06. Der Kullback-Test stellt jedoch keine Differenz fest. Dies ist zurückzuführen auf die Größe der Gruppen, die zu klein ist, um Gruppen mit Varianzen zwischen 5’² und 7’² zu unterscheiden.

3. Test auf

3. Tests auf allen sechs Spalten

Dieses Mal werden alle sechs Spalten ausgewählt. In der Registerkarte „Ausgabe“ fordern wir Korrelations- und Kovarianzmatrizen.

Die Tests der Mittelwerte führen zu ähnlichen Ergebnissen wie im Fall 2 (siehe oben). Die Differenz zwischen G1 und G2 basierend auf dem Mahalanobis-Abstand ist etwas kleiner.

Dennoch sind die Tests der Kovarianzmatrizen überraschenderweise unterschiedlich. Kleine Differenzen, die auf den ersten 3 Spalten beobachtet werden, und die größeren, die auf den letzten 3 Spalten beobachtet werden, häufen sich an. Darüber hinaus gibt es nicht zu vernachlässigende Kovarianzen zwischen RV1 und RV4, zwischen RV2 und RV5 und zwischen RV3 und RV6. Schließlich erhält man signifikante Differenzen, wenn der Test auf allen 6 Spalten durchgeführt wird.