Quel outil de validation de méthodes choisir ?

Quel outil de validation de méthodes choisir ?

Ce guide décrit des outils de validation de méthodes et vous aidera à choisir la méthode adaptée à vos besoins.

Toutes les méthodes mentionnées ci-dessous se trouvent dans le menu XLSTAT Validation de Méthodes, à l’exception de la régression linéaire, qu’on retrouve dans le menu modélisation des données, les tests de corrélation qui font partie du menu tests de corrélation / d’association, ainsi que les fonctionnalités d’analyse de systèmes de mesure (Gage R&R), qui se trouvent dans le menu Maîtrise Statistique des Procédés (SPC).

Qu’es-ce que la comparaison de méthodes ?

Les outils de comparaison de méthodes permettent d’étudier la concordance entre deux méthodes de mesure d’un même paramètre. Ils sont largement utilisés dans le monde médical, lors du développement d'instruments de mesure pour remplacer des instruments mesurant le même paramètre, mais plus coûteux, invasifs ou chronophages. Plusieurs aspects peuvent être abordés, notamment les limites d’agrément (Limits of Agreement), ainsi que les biais (ou erreurs) constant et proportionnel.

Les méthodes développées ci-dessous ne fonctionnent que sur des variables quantitatives. D'autres méthodes statistiques telles que le Kappa de Cohen sont adaptées pour l’étude de la concordance entre deux méthodes mesurant des variables qualitatives ou catégorielles.

Analyse de Bland-Altman : évaluer le biais constant et les limites d’agrément

L'analyse de Bland-Altman permet d'évaluer la concordance entre deux méthodes de mesure. Comparons deux méthodes (A et B) visant à mesurer un résultat clinique. Le résultat est mesuré en utilisant la méthode A et la méthode B sur 50 patients.

Dans le nuage de points ci-dessous, nous représentons la méthode B sur l'axe des Y et la méthode A sur l'axe des X. Chaque point correspond à un patient. Idéalement, les points devraient être agrégés autour de la ligne à 45 ° (Y = X). Dans le graphique ci-dessous, la plupart des mesures de la méthode B semblent être décalées vers le haut par rapport à la méthode A. Il s'agit d'un biais constant systématique. Plus loin, nous aborderons un autre type de biais, le biais proportionnel.

Bien que cette approche ne soit pas recommandée, la concordance entre deux méthodes a souvent été évaluée via une analyse de corrélation, une corrélation élevée indiquant une bonne concordance. L'analyse de corrélation comporte des limites lorsqu'elle est utilisée pour comparer deux méthodes. Par exemple, elle ne tient pas compte des biais constants ou proportionnels.

L'analyse de Bland-Altman permet une analyse plus approfondie de l'accord et aide à mesurer avec précision le biais constant. Parmi les résultats de cette analyse, on peut trouver le graphique de Bland et Altman, représenté la plupart du temps de la manière suivante :

• Axe des Y : Différence entre les deux méthodes pour chaque unité statistique (patients dans notre cas).
• Axe des X : Moyenne entre les deux méthodes pour chaque unité statistique.

La ligne horizontale noire Y = 0 est la ligne idéale d’absence de différence entre les deux méthodes. Les lignes bleues représentent le biais constant avec son intervalle de confiance à 95%. Les lignes rouges représentent l'intervalle de confiance à 95% des différences, autrement dit les limites d'agrément à 95% entre les deux méthodes. Cela signifie que les différences entre les deux méthodes se situeront entre ces deux limites 95% des fois. L'acceptabilité de cette fourchette doit généralement être déterminée par les utilisateurs a priori en fonction de leur domaine d'expertise.

L'analyse de Bland-Altman permet également de détecter la présence d’un biais proportionnel, qui se traduit par une dépendance entre les différences et les valeurs de la mesure. Dans le nuage de points ci-dessous, la méthode B donne des valeurs de mesure plus faibles que la méthode A à faibles niveaux de mesure (partie gauche du graphique). A l’opposé, lorsque les valeurs de mesure sont élevées, la méthode B surestime les valeurs par rapport à la méthode A (partie droite du graphique). Ce biais proportionnel peut clairement être détecté sous forme d'une tendance linéaire dans le graphique de Bland-Altman. De nombreux autres résultats et options sont disponibles dans la fonctionnalité Bland-Altman. Par exemple, il est possible de travailler sur les différences en pourcentage plutôt que les différences brutes sur l'axe des Y. Ceci est utile lorsque la variabilité des différences augmente en fonction des valeurs du paramètre mesuré. Comment mesurer les biais constants et proportionnels lors de la comparaison de deux méthodes ?

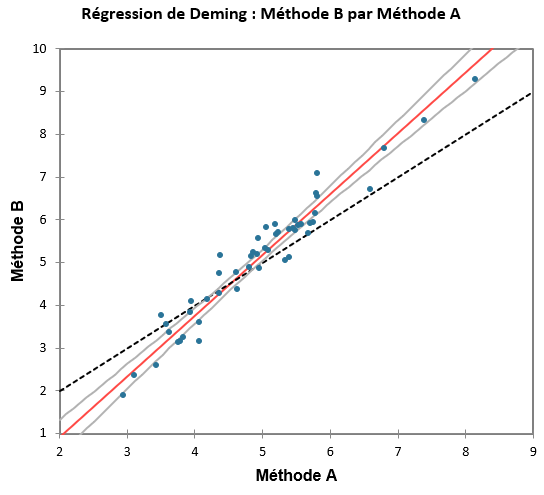
Régressions de Deming et de Passing-Bablok : quantifier les biais constant et proportionnel

Afin de quantifier les biais constants et proportionnels entre deux méthodes, il est possible d’exécuter une régression linéaire simple avec une méthode comme variable dépendante et la deuxième comme indépendante. Cependant, la régression linéaire classique présente un inconvénient majeur dans cette situation. L'une des hypothèses de la régression linéaire est que la variable indépendante n'est pas soumise à une erreur de mesure. Des outils de régression adaptés ont été développés pour résoudre ce problème. Ces techniques incluent la régression de Deming ainsi que la régression de Passing et Bablok. Les deux méthodes ajoutent un terme d'erreur à chacune des variables Y et X.

Tout comme la régression linéaire simple classique, les régressions Deming et de Passing-Bablok estiment une constante et une pente à partir desquelles les biais constant et proportionnel peuvent être évalués :

La constante estimée représente le biais constant, dont la significativité peut être évaluée en examinant l'intervalle de confiance associé : s’il inclut zéro, le biais est non-significatif. S’il n’incult pas zéro, le biais est significatif.

Le biais proportionnel est représenté par la différence entre la pente de régression et la pente de la ligne Y = X, qui est égale à 1. L'importance de ce biais peut être évaluée en vérifiant si l'intervalle de confiance associé à la pente de régression comprend la valeur 1 (non significatif) ou non (significatif).

Deming ou Passing-Bablok ?

La régression de Deming est paramétrique et, en tant que telle, comporte des hypothèses relativement strictes à respecter, en comparaison avec la régression de Passing-Bablok, qui elle est non-paramétrique. Par exemple, les résidus d'une régression de Deming doivent suivre une distribution normale, et la régression de Passing-Bablok est moins sensible aux valeurs hors-normes.

Lorsque la variabilité des différences change en fonction de la taille de la mesure, la régression de Deming peut être adaptée et devient une régression de Deming pondérée (activez erreurs proportionnelles dans la boîte de dialogue). De plus, si les variances des méthodes de mesure sont connues, elles peuvent être introduites manuellement dans l'onglet Options.

La régression de Passing-Bablok peut être adaptée à des instruments mesurant le même paramètre mais sur des échelles différentes, et avec une corrélation potentiellement négative (activer la part III – échelles différentes dans l'onglet options).

Répétabilité, reproductibilité et graphiques de Youden

Pour étudier la répétabilité et la reproductibilité avec XLSTAT, nous recommandons d'utiliser les fonctionnalités d’analyse de systèmes de mesure (Gage R&R) pour les données quantitatives ou pour les attributs. Ces outils se trouvent dans le menu Maîtrise Statistique des Procédés (MSP).

Cependant, les graphiques de Youden sont remarquablement efficaces pour étudier visuellement et intuitivement la reproductibilité inter-laboratoire et la répétabilité intra-laboratoire pour une certaine mesure. De plus, l'analyse de Bland-Altman permet de quantifier la répétabilité de chaque méthode, à condition que l'utilisateur fournisse plusieurs mesures appariées par unité statistique – chaque unité pouvant être un patient ou un opérateur par exemple (utilisez le champ Groupes).