Lancer une analyse XLSTAT Cloud
Dans ce tutoriel nous allons dans un premier temps générer un échantillon aléatoire tiré dans la loi normale et un dans une loi Uniforme. Par la suite nous allons réaliser des tests de normalités sur les deux échantillons en utilisant XLSTAT Cloud.
Jeu de données pour l'échantillonnage d'une distribution et test de normalité
Dans ce tutoriel nous vous montrons comment générer un échantillon aléatoire tiré dans une loi Normale (de moyenne 2, et d'écart type (sigma) = 2), puis dans une loi Uniforme entre -1.5 et 5. Pour réaliser cette tâche, nous allons utiliser la fonctionnalité Echantillonnage dans une distribution dans le menu Préparation des données.
Faire un échantillonage d'une distribution avec XLSTAT Cloud
Après avoir ouvert XLSTAT Cloud, cliquez sur Echantillonnage dans une distribution dans le menu Préparation des données.

Une fois après avoir cliqué sur le bouton, la fenêtre de la fonctionnalité Echantillonnage dans une distribution apparaît.
Sélectionnez la Distribution théorique dans la première liste déroulante et ensuite la loi dans la deuxième liste déroulante afin de l’utiliser et de définir les paramètres. Dans notre cas, sélectionnez la loi Normale, qui est le choix par défaut.
Renseignez ensuite les paramètres de la loi dans les champs prévus à cet effet puis le nombre d’échantillons à générer ainsi que leurs tailles.
L’interface affichée ci-dessous correspond à la génération d'un échantillon de 1000 individus à partir d'une loi N(2,2).

Une fois que vous avez cliqué sur le bouton Lancer, l'échantillon est affiché dans une nouvelle feuille.
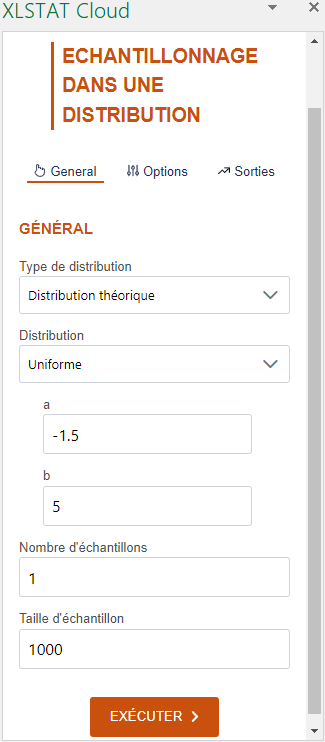
Nous allons ensuite générer un second échantillon qui suit une loi uniforme entre -1.5 et 5. Pour ce faire il faut sélectionner la loi Uniforme dans la deuxième liste déroulante et renseigner les paramètres, à savoir -1.5 et 5.
L’interface affichée ci-dessous correspond à cette génération.
Dans l’onglet Sorties, désactivez Afficher l’en-tête du rapport et dans l’onglet Options, sélectionnez l’option d’affiche Plage dans la liste déroulante qui permet de choisir un endroit pour afficher notre échantillon. Choisir comme plage d’affichage la première cellule à côté du haut de la colonne du premier échantillon. Cette manipulation permet d’afficher le deuxième échantillon juste à côté du premier.


Cliquez sur Lancer et le second échantillon est affiché.
Paramétrer un test de la normalité avec XLSTAT Cloud
La prochaine étape est de tester la normalité des deux échantillons générés. Cliquez sur Tests de normalité dans le menu Description de données.
Une fois après avoir cliqué sur le bouton, la fenêtre de la fonctionnalité Tests de normalité apparaît.

Sélectionnez les deux échantillons générés précédemment dans le champ Données, il faut également activer l’option Libellés des échantillons.
Pour sélectionner des données, il faut dans un premier temps sélectionner la plage de données sur la feuille de calcul et ensuite cliquer sur la flèche située à droite du champ de saisi que l’on souhaite remplir. La sélection se fera automatiquement.

Dans l’onglet Sorties, activez l’affichage des Graphiques Q-Q (loi normale) afin de nous permettre de visualiser l'écart à la normalité des échantillons

Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués et les résultats sont affichés sur une nouvelle feuille.
Interprétation des résultats des tests de normalité
Les résultats sont d'abord fournis pour le premier échantillon, puis pour le second.
Le premier résultat affiché est le Q-Q plot pour le premier échantillon. Le Q-Q plot permet de comparer la fonction de répartition de l'échantillon (en abscisses) à celle qu'aurait une loi normale théorique de même moyenne et même variance (en ordonnées). Dans le cas d'un échantillon issu d'une distribution normale, on doit observer un alignement presque parfait avec la première bissectrice du plan. Dans le cas contraire des écarts doivent être observés.

Nous voyons ici que la fonction de répartition empirique est très proche de la bissectrice.

Les tests de Shapiro-Wilk et de Jarque-Bera confirment que l'on ne peut pas rejeter l'hypthèse de normalité de l'échantillon (p > alpha). On notera qu'avec le test de Shapiro-Wilk, le risque de se tromper en rejetant l'hypothèse serait plus important qu'avec le test de Jarque-Bera.
Les résultats qui suivent concernent le second échantillon, avec dans un premier temps, le Q-Q plot.
Contrairement à ce que nous avons observé pour le premier échantillon, nous remarquons ici un fort écart à la normalité.

Cet écart est confirmé par les tests ci-dessous qui permettent d'affirmer sans hésitation que l'on doit rejeter l'hypothèse de normalité de l'échantillon.

En conclusion, dans ce tutoriel, nous avons vu comment générer deux échantillons, l'un suivant une loi normale, l'autre suivant une loi uniforme. Nous avons ensuite appliqué sur ces deux échantillons les tests de Shapiro-Wilk et Jarque-Bera : nous avons vu que les tests ont n'ont pas rejeté l'hypothèse de normalité pour le premier échantillon, alors qu'ils l'ont infirmée pour le second échantillon.
Notez qu'aucune de vos données n'est stockée lorsque vous utilisez le module XLSTAT-Cloud.
Cet article vous a t-il été utile ?
- Oui
- Non