Coefficient de corrélation de Pearson dans Excel

Ce tutoriel explique comment calculer et interpréter le coefficient de corrélation de Pearson pour des variables quantitatives sous Excel en utilisant XLSTAT.

Jeu de données pour calculer le coefficient de corrélation de Pearson

Les données représentent un échantillon de clients d’une boutique de vente de chaussures en ligne décrits par différentes variables (par exemple le montant de la facture, la pointure…).

But de ce tutoriel

L’objectif est d’étudier les corrélations entre le montant dépensé et les diverses caractéristiques des clients. Nos données sont quantitatives continues. Une option est donc de nous orienter vers le coefficient de corrélation de Pearson. Un coefficient de corrélation mesure la force de la liaison (positive ou négative) qui peut exister entre deux variables quantitatives.

Nous testerons également la significativité des corrélations et générer les sorties suivantes :

• Une matrice de corrélation pour visualiser l’ensemble de coefficients de corrélations sous forme d’une matrice,

• Une matrice des nuages de points pour afficher les nuages de points pour toutes les combinaisons possibles de variables deux à deux.

Un peu de théorie : Comment calculer le coefficient de corrélation de Pearson ?

Aujourd'hui, beaucoup de calculateurs en ligne de coefficients de corrélation sont disponibles, mais vous pouvez facilement calculer le coefficient de corrélation par vous-même.
Le coefficient de corrélation de Pearson se calcule avec la formule suivante :

Comment interpréter la corrélation ?

Plus sa valeur est proche de -1, plus fort est le lien négatif entre les variables : quand l'une augmente, l'autre diminue.
Plus sa valeur est proche de 1, plus fort est le lien positif entre les variables : les deux variables augmentent ou diminuent simultanément.
Si le coefficient de corrélation est proche de 0, cela signifie qu'il n'y a pas de lien entre les deux variables.

Comment tester la significativité ?

Une statistique de test est calculée avec la formule ci-dessous qui suit une distribution de Student à n-2 degrés de liberté.

Si ces valeurs dépassent les bornes définies par le seuil alpha=0.05, alors l'hypothèse nulle est rejetée et le coefficient de corrélation de Pearson est significativement différent de 0.

Paramétrer le calcul du coefficient de corrélation de Pearson avec XLSTAT

• Ouvrez XLSTAT

• Sélectionnez la commande Tests de Corrélation/Association / Tests de corrélation

• Dans l’onglet Général de la boîte de dialogue affichée, sélectionnez les colonnes A-E dans le champ Observations/Variables quantitatives. Ensuite, choisissez Pearson comme type de corrélation à utiliser pour les calculs.

• Dans l’onglet Sorties, activez l'affichage des p-values, les coefficients de détermination (R2), ainsi que le filtrage et le tri des variables selon leur R2.

• Cliquez sur OK pour lancer les calculs.

Comment interpréter les résultats du calcul du coefficient de corrélation de Pearson ?

Les premiers résultats dans XLSTAT sont les statistiques descriptives de toutes les variables (moyenne, écart-type etc.). La matrice de corrélation suivie des intervalles de confiance (95%) sont affichés dans les tableaux ci-dessous :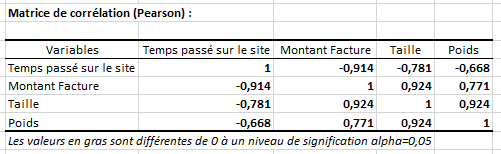

Les coefficients de corrélation varient entre -1 et 1. Une valeur positive indique une corrélation positive. Une valeur négative reflète une corrélation négative. Une valeur proche de zéro reflète l’absence d'une corrélation linéaire.

Par exemple, la paire Facture et Taille est caractérisée par une corrélation positive et forte (0,924). A contrario, nous pouvons conclure que plus les clients passent du temps sur le site moins ils dépensent d'argent (-0,914).

A noter que la variable Pointure a été exclue par les sorties puisque sa somme des R2 avec toutes les autres variables est minimale.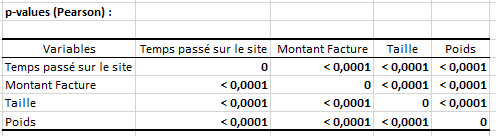
Tous les coefficients sont significatifs au seuil de significativité de 0,05 (p < 0,05). Cela signifie que le risque de rejeter l'hypothèse nulle alors qu’elle est vraie est inférieur à 5%. Ceci est confirmé par le tableau des p-values ci-dessus (toutes les p-values sont inférieures à 0.0001).
Les coefficients de détermination correspondent aux coefficients de corrélation au carré. Ils mesurent la force de la corrélation, qu'elle soit négative ou positive. Ici, en utilisant l'option "filtrer les variables", nous avons choisi de représenter seulement les 4 variables dont la somme du R2 avec d'autres variables est la plus élevée.
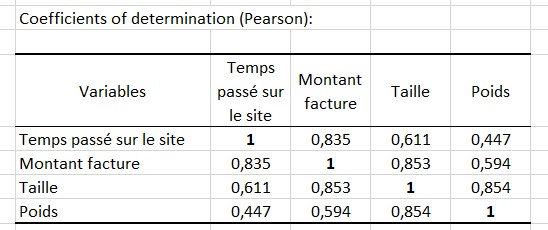De plus, nous avons trié les variables avec le BEA (Bond Energy Algorithm). Cette méthode applique une permutation sur les lignes et les colonnes d'une matrice carrée afin de placer les colonnes dont les lignes ont des valeurs similaires côte à côte.

La carte de corrélation au-dessus s'appuie sur une échelle de couleurs allant du bleu au rouge (échelle froid-chaud) pour l'affichage des corrélations. La couleur bleue correspond à une corrélation négative proche de -1 (ex : Temps passé sur le site vs Facture) et la couleur rouge correspond à une corrélation positive proche de 1 (ex : Taille vs Facture).

La matrice de graphiques au-dessus affiche un histogramme par variable (sur la diagonale) et un nuage de points pour toutes les paires possibles de variables.

L’histogramme révèle les caractéristiques de la distribution d’une variable. Le nuage de points reflète le signe et la force d’une corrélation. Pour le signe, nous pouvons utiliser la couleur des points ainsi que la pente de la droite de régression. Pour la force, il suffit d'observer la dispersion des points autour la droite. Par exemple, nous pouvons suggérer que la Pointure a une très faible relation linéaire avec les autres attributs (dernière colonne de la matrice).

Aller plus loin : explorer des variables quantitatives avec une Analyse en Composantes Principales

L’analyse en Composantes Principales (ACP) est une méthode d’analyse multivariée qui permet d'explorer facilement une matrice de corrélations. Elle permet également de mieux comprendre la structure de nos données et la relation entre les observations (clients) et les variables. Un avantage de l'ACP est la représentation graphique synthétique des résultats (cercle de corrélation, biplot…).