Régressions Lasso et Ridge avec Excel

Ce tutoriel vous guidera dans la mise en place et l’interprétation d’une régression Lasso et d’une régression Ridge dans Excel à l’aide de XLSTAT-R.

Quelques mots sur les régressions Lasso et Ridge

Dans les cas de régression où le nombre de prédicteurs est très élevé, les régressions Ridge et Lasso ont été proposées pour fournir des estimations plus précises des coefficients par rapport aux approches plus classiques. Ridge et Lasso ajoutent un terme dit de régularisation à la fonction de coût de la régression. Ce terme pénalise la fonction de coût lorsque la somme des valeurs absolues des coefficients augmente. Dans le cadre de la régression Lasso, ce terme est appelé norme L1 et est proportionnel à la somme des coefficients pris en valeur absolue (somme des |beta|). Dans le cadre d’une régression Ridge, le terme est appelé norme L2 ou régularisation de Thikhonov et est proportionnel à la somme des carrés des coefficients (somme des ||beta||²).

Alors que la régularisation Ridge a tendance à rapprocher les coefficients de zéro sans toutefois les annuler, la régularisation Lasso peut aussi rendre certains coefficients nuls.

Une technique intermédiaire, appelée Elastic Net, a également été proposée pour surmonter certaines limitations de chacune des régularisations Ridge et Lasso.La régularisation peut être contrôlée grâce à un paramètre de calibration appelé Lambda. La force de régularisation augmente avec Lambda.

Dans l’univers du Machine Learning, les régularisations Lasso et Ridge sont également appelées des techniques de weight decay (dégradation des poids). Les régressions Ridge, Lasso et Elastic Net peuvent toutes être utilisées lorsque le nombre de prédicteurs est supérieur au nombre d’observations.

La fonction Ridge/Lasso/Elasticnet développée dans XLSTAT-R appelle la fonction glmnet de la librairie glmnet dans R (Jerome Friedman, Trevor Hastie, Noah Simon, Junyang Qian, Rob Tibshirani).

Jeu de données pour exécuter des régressions Ridge et Lasso avec XLSTAT-R

Les données ont été simulées et correspondent à 36 échantillons biologiques d’individus sains et malades de 3 génotypes différents. Pour chaque échantillon, l’expression de 1561 gènes est mesurée par quantification des ARN. Plus de détails ici. Pour une meilleure lisibilité des coefficients dans les résultats, il est recommandé de labelliser les réponses binaires en 0 et 1. Ici, les patients sains sont labellisés 0 et les individus malades sont labellisés 1.

L’objectif est d’identifier les gènes ayant l’influence la plus importante sur la variable Sain-Malade. Ceci est équivalent à une étude d’expression différentielle. Nous utiliserons une régression Lasso suivie d’une régression Ridge puis comparerons les résultats. La régression logistique ne peut être utilisée ici parce que le nombre de variables (gènes) est bien plus élevé que le nombre d’observations (échantillons).

Paramétrer une régression Lasso dans XLSTAT-R

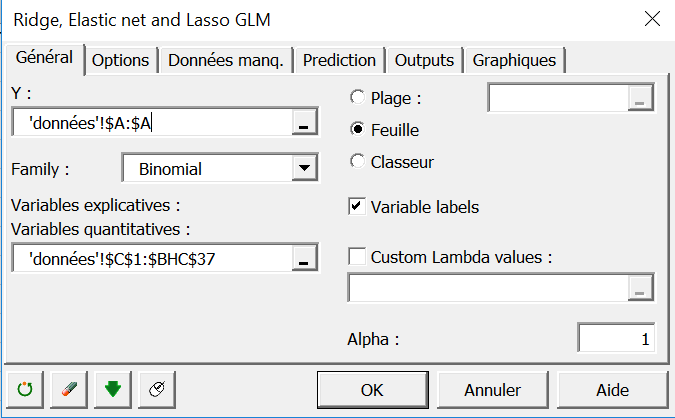Allez dans XLSTAT-R / glmnet / Ridge, Elastic net and Lasso GLM(glmnet) Dans l’onglet général, sélectionnez la variable de statut (sain/malade) dans le champ Y. La réponse est binaire. Sélectionnez donc Binomial dans la liste family. Sélectionnez toutes les données d’expression dans le champ variables explicatives quantitatives. Le paramètre alpha contrôle le type de pénalisation à appliquer. Zéro correspond à Ridge, 1 à Lasso et les valeurs intermédiaires à Elastic Net. Entrez 1 pour le moment.

Dans l’onglet options, assurez-vous d’activer l’option standardize afin d’appliquer une standardisation des données avant les calculs. Paramétrez le champ number of Lambda values à 100. R lancera un modèle sur 100 valeurs de lambda et utilisera une validation croisée k-fold pour identifier une valeur optimale. Activez tous les graphiques dans l’onglet Graphiques. 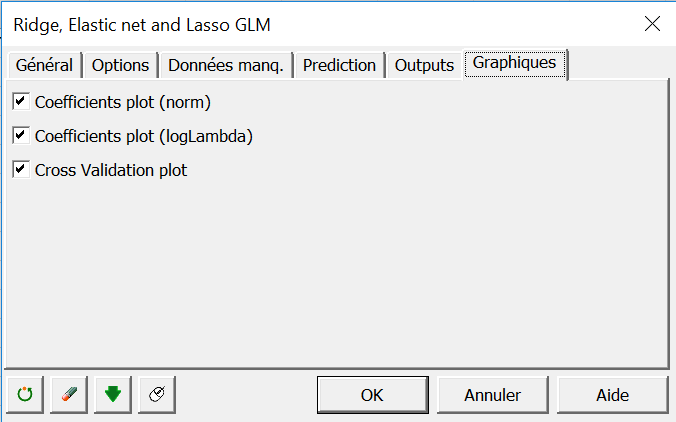Cliquez sur OK pour lancer les calculs.

Régression Lasso : Interprétation des sorties

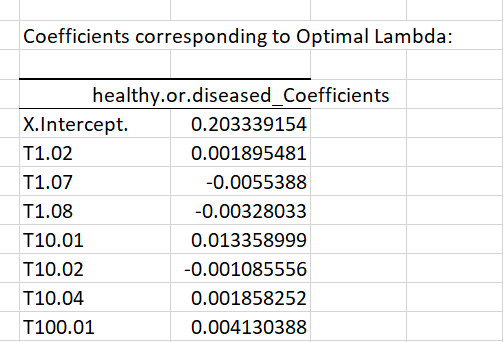
D’abord, la valeur de lambda minimisant la déviance est affichée. Il s’agit de la valeur optimale de lambda déterminée par la validation croisée. Ceci est suivi par les coefficients correspondants calculés sur tous les gènes : 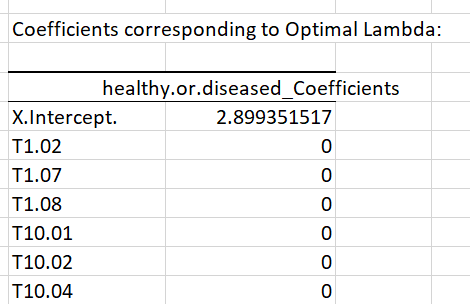La pénalisation Lasso a réduit la majorité des coefficients à zéro. Ceci peut aider à déterminer les gènes les plus influents pour la réponse, comme le gène T106.02 par exemple. Comme la réponse est binaire, les coefficients doivent être interprétés en tant que log-odds. Le signe positif reflète le fait que le gène T106.02 semble être plus exprimé chez les patients malades que chez les patients sains (rappel : les patients malades sont affectés au statut 1 dans le jeu de données). 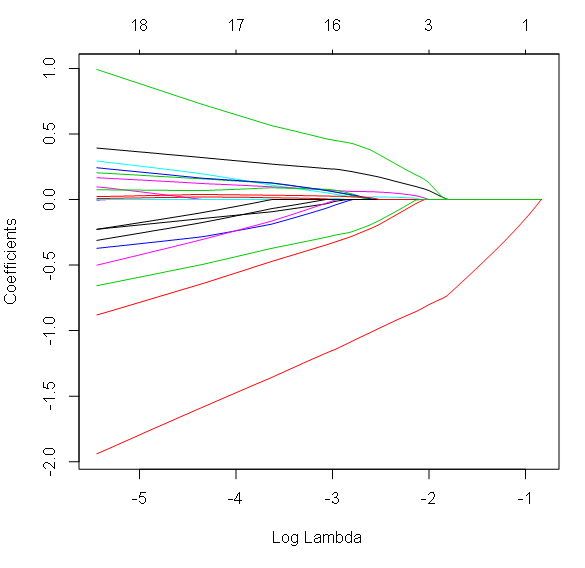Le graphique Coefficients plot avec les valeurs de Log Lambda sur l’axe des abscisses montre la détérioration des valeurs de coefficients avec l’augmentation du terme de pénalisation lambda (ou son logarithme). Un grand nombre de coefficients deviennent nuls pour des valeurs élevées de lambda. Les chiffres en haut du graphique sont les nombres de coefficients restants pour la valeur de log lambda correspondante. 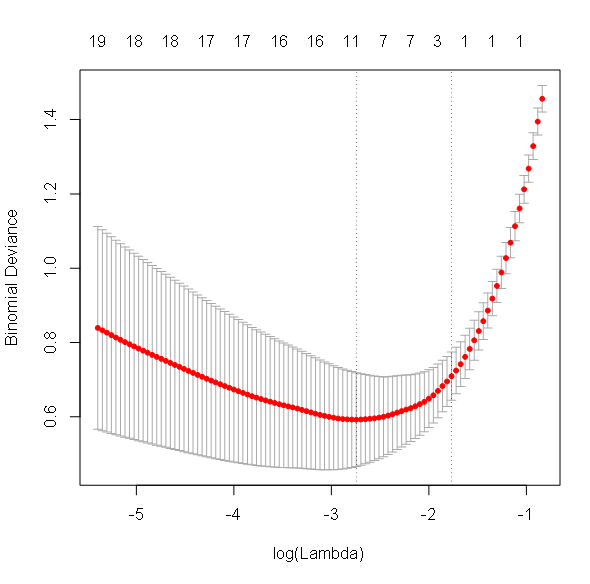Le graphique Cross Validation plot montre les résultats de la validation croisée. La déviance (ou erreur) est affichée en fonction des valeurs de lambda. La valeur optimale de lambda correspond à la valeur de lambda au minimum de cette fonction. Notez que le logarithme utilisé pour lambda ici est le logarithme népérien. Comparons ces sorties aux sorties d’une régression Ridge à présent.

Paramétrer une régression Ridge avec XLSTAT-R

Revenez à la boîte de dialogue glmnet et introduisez 0 pour le paramètre alpha. 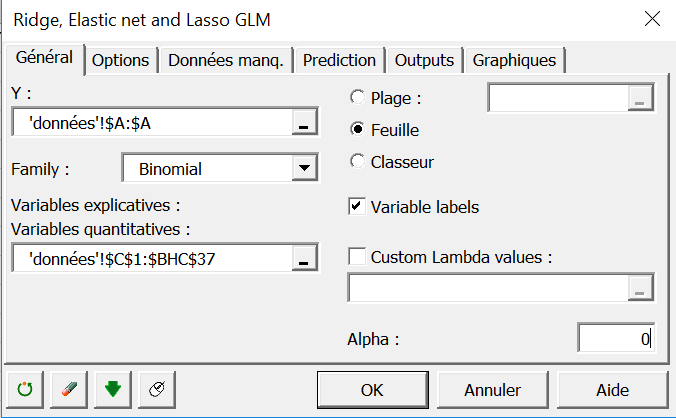Cliquez OK.

Régression Ridge : interprétation des résultats

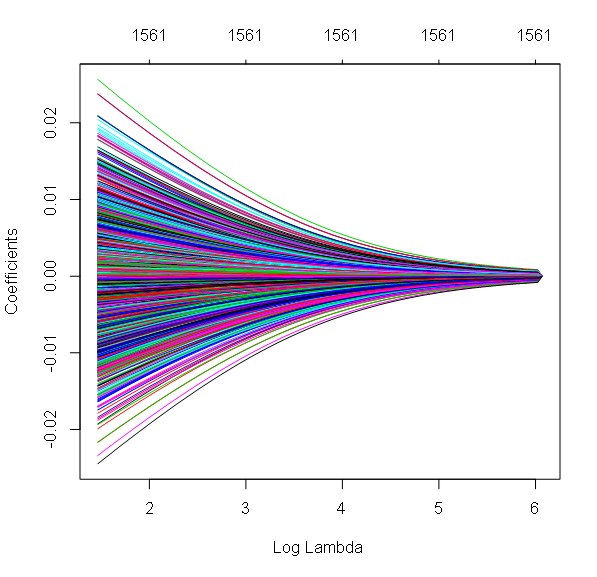
Contrairement à la régression Lasso, la régression Ridge a attribué une valeur non-nulle de coefficient à tous les prédicteurs. Cependant, ces coefficients ont été rapprochés de zéro. Et ce rétrécissement est d’autant plus important que le paramètre de régularisation Lambda est élevé. Cela peut se constater sur le graphique des coefficients :