Modèles de classification par les Classes Latentes dans Excel

Modèles de classification par les classes latentes

Dans ce tutoriel, nous utiliserons XLSTAT-LatentClass pour estimer et interpréter un modèle de classification par les classes latentes avec 4 indicateurs (variables) catégoriels. Pour aller plus loin, cf. McCutcheon (1987), Magidson et Vermunt (2001) et Magidson et Vermunt (2004).

Ce tutoriel implique :

• La mise en place et l’estimation de modèles de classification par les classes latentes
• La recherche des modèles qui s’ajustent le mieux aux données
• L’interprétation des sorties et graphiques
• L’obtention d’équations de régression pour la classification de nouveaux cas

Jeu de données pour l'estimation de modèles de classification par les classes latentes avec XLSTAT

Les données (Figure 1) constituent des observations de 4 variables catégorielles (objectif, précision, compréhension et coopération) sur 1202 individus (cas). La variable frq représente le nombre d’occurrences du profil de réponse parmi les répondants (somme de cette colonne = 1202).

Figure 1: en-tête du tableau de données*

* Source: 1982 General Social Survey Data National Opinion Research Center (USA)

But de ce tutoriel sur les modèles de classification par les classes latentes

Identifier des typologies (classes) distinctes de répondants à des sondages. Les cas sont sondés pour obtenir leur opinion sur l’objectif des sondages (variable objectif) et leur précision (variable précision). Deux variables sont évaluées par le sondeur pour chaque répondant : l’évaluation du degré de compréhension (variable compréhension) et de coopération (variable coopération) de la personne sondée pendant l’interview.

Plus précisément, nous nous focaliserons sur les critères de choix du nombre de classes et sur la manière dont les répondants sont assignés à ces classes.

Paramétrer un modèle de classification par les classes latentes avec XLSTAT

Aller sur XLSTAT / XLSTAT-LatentClass / Classification par les classes latentes (Figure 2).

Figure 2 : menu XLSTAT-LatentClass.

Une fois le bouton cliqué, la boîte de dialogue des modèles de classification par les classes latentes avec XLSTAT-LatentClass apparaît (Figure 3).

Figure 3 : Boîte de dialogue des modèles de classification par les classes latentes (onglet Général).

Pour cette analyse, nous utiliserons les 4 variables (objectif, précision, compréhension et coopération) en tant qu’indicateurs. La variable frq regroupe toutes les réponses similaires sur une seule ligne (ce qui réduit considérablement la taille du tableau de données). Nous l’utiliserons donc en tant que poids des observations. Un tableau équivalent contenant 1202 lignes correspondant aux 1202 réponses sur les 4 variables donnerait les mêmes résultats.

Les 4 indicateurs étant catégoriels, nous les sélectionnons dans le champ Observations / Nominales.

Sélectionner la variable frq dans le champ Poids des observations.

Afin de déterminer le nombre de classes, nous estimerons 4 modèles différents de classification, chaque modèle correspondant à un nombre différent de classes. Il est recommandé de démarrer avec les modèles renfermant entre 1 et 4 classes (donc 4 modèles au total).

Sous l’option Nombre de Classes, taper 1 dans « de » et 4 dans « à ». Ceci engendrera l’estimation de 4 modèles (modèle à 1 classe, modèle à 2 classes, modèle à 3 classes et modèle à 4 classes).

Ci-dessous l’onglet général de la boîte de dialogue paramétrée :

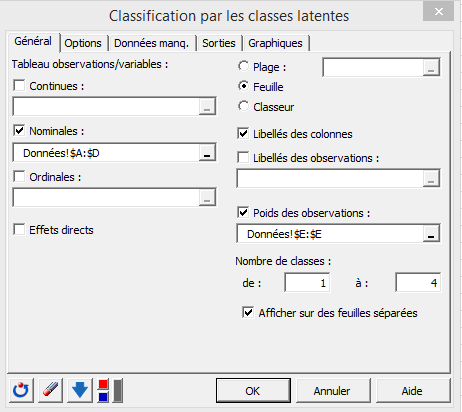
Figure 4 : Boîte de dialogue paramétrée.

Les calculs démarrent dès que vous cliquez sur OK.

Interpréter les sorties d’un modèle de classification par les classes latentes

A la fin des calculs, XLSTAT-LatentClass produit 5 feuilles Excel : une feuille résumé (Classification par les classes) suivie d’une feuille pour chacun des 4 modèles estimés.

La feuille Classification par les classes contient un résumé de tous les modèles estimés. La statistique V² reflète la part d’association entre les variables non expliquée après l’estimation du modèle. Plus cette valeur est faible, meilleur est l’ajustement du modèle. Une manière de déterminer le meilleur modèle parmi les modèles estimés est d’inspecter deux chiffres : 1) la p-value, sous l’hypothèse que la statistique V² suit une distribution du khi-2 ; 2) le nombre de paramètres. Le meilleur modèle est le modèle le plus parcimonieux (impliquant le plus petit nombre de paramètres) associé à un bon ajustement (p > 0.05). Dans notre cas, le meilleur modèle est le modèle à 3 classes, contenant 20 paramètres (p = 0.105).

Les critères d’information BIC, AIC et AIC3, plus globaux, favorisent également les modèles parcimonieux associés à un bon ajustement, sans nécessairement que la statistique V² suive une distribution du khi-2. Par ailleurs, ces critères restent valides si un ou plusieurs indicateurs est continu ou si les données sont clairsemées à cause d’un grand nombre d’indicateurs. Le meilleur modèle parmi les modèles estimés est celui associé à la valeur de critère la plus faible, quel que soit le critère d’information. Par exemple, le modèle associé au BIC le plus faible est encore une fois le modèle à 3 classes (BIC = 5651,121).

Figure 5. Statistiques pour chaque modèle.

Inspectons à présent les sorties propres au modèle à 3 classes (feuille LCC-3 Classes).

Après des statistiques descriptives, diverses sorties associées au modèle à 3 classes sont affichées. Tout en bas, vous trouverez le Profil (Figure 6) qui renferme les paramètres du modèle pour chaque classe (sous forme de probabilités conditionnelles).

Figure 6. Profil du modèle à 3 classes.

Les classes sont automatiquement ordonnées suivant leurs tailles. La première classe contient 62% des individus, la deuxième 20% et la troisième 3%. Les probabilités conditionnelles mettent en relief les contrastes entre les classes en termes de profils de réponses. Par exemple, les individus appartenant à la troisième classe ont une forte probabilité de considérer que les sondages constituent une perte de temps (la modalité 3 de la variable « objectif » correspond à « perte de temps ») et que les résultats des sondages ne sont pas crédibles (ce qui correspond à la modalité 2 de précision) en comparaison aux individus appartenant aux deux autres classes. Ceci peut être visualisé sur le graphique qui suit (Profil des classes, Figure 7).

Figure 7: Profil des classes pour le modèle à 3 classes.

Classification des individus selon une assignation modale

Faire défiler vers le bas pour afficher les sorties portant sur la classification (Figure 8).

Figure 8: Classification des individus selon le modèle à 3 classes

La première ligne du tableau de classification montre que tous les individus dont le profil de réponse correspond à [objectif = 1 (bon) ; précision = 1 (bonne) ; compréhension = 1 (bonne) et coopération = 1 (bonne)] sont classés au sein de la classe 1 (colonne « Classe ») car la probabilité d’appartenir à cette classe est la plus élevée (0,920).

Notez qu’une classification des individus via un assignement modal engendre une certaine part d’erreur de classification. L’erreur de classification attendue peut être calculée en effectuant une classification croisée entre les classes modales et les classes « réelles » (ou probabilistes, ou proportionnelles). Ceci peut se faire via le tableau de classification - Modale (plus haut dans la feuille de résultats). Pour ce modèle, l’assignation modale classifie correctement 704 cas au sein de la classe 1, 163,8 cas au sein de la classe 2 et 176,2 au sein de la classe 3, ce qui donne un total attendu de 1044,085 classifications correctes sur les 1202 individus. Ceci représente une erreur de classification de 13.13% [(1 – 1044,085)/1202].

Figure 9 : Tableau de classification – Modale (modèle à 3 classes).

Notez également que les tailles attendues de classes ne sont jamais retrouvées parfaitement via l’assignation modale. Le tableau de classification (figure 9) montre que 67% des individus (805 sur 1202) sont assignés à la classe 1 suivant l’assignation modale, en comparaison avec les 61,7% attendus. (si les individus étaient assignés aux classes proportionnellement aux probabilités d’appartenance, 61,7% seraient assignés à la classe 1).

Interprétation des résidus bivariés

Les résidus bivariés sont des mesures locales du degré d’association des paires d’indicateurs pris deux à deux selon le modèle (Figure 10).

Figure 10 : Résidus bivariés associés au modèle à 3 classes.

Les résidus bivariés correspondent à des khi-2 de Pearson divisés par le nombre de degrés de liberté. Le khi-2 est calculé sur les effectifs observés au sein d’un tableau à deux voies basé sur les effectifs attendus estimés via le modèle. Les résidus bivariés ne devraient pas dépasser 1 de manière importante. Le résidu bivarié de 2,4 (Figure 10) suggère que le modèle à 3 classes reproduit mal l’association entre compréhension et coopération.

En comparaison, les résidus bivariés associés au modèle à 4 classes (Figure 11) sont tous inférieurs à 1. Ceci suggère que le modèle à 4 classes pourrait avoir un meilleur ajustement que le modèle à 3 classes. Ainsi, les modèles à 3 et 4 classes peuvent être justifiées, le modèle à 3 classes étant justifié par le BIC et celui à 4 classes par les résidus bivariés.

Figure 11 : Résidus bivariés associés au modèle à 4 classes.

Equation de scoring

Nous pouvons utiliser l’équation de scoring pour obtenir les équations de régression, afin de classer de nouveaux cas.

Figure 12 : Equation de scoring associée au modèle à 3 classes.

Chaque profil de réponse est associé à un score au sein de chaque classe, et est assigné à la classe au score le plus élevé. Par exemple, pour le profil d’Obs1, nous avons :

Objectif = 1 ; précision = 1 ; compréhension = 1 ; coopération = 1.

Scores logit correspondants (calculés d’après les lignes en jaune) :

Classe 1 = 2,916 ; Classe 2 = 0,457 ; Classe 3 = -3,373.

Ainsi, ce profil est assigné à la classe 1 (score logit le plus élevé). Afin d’obtenir des scores plus parlants, il est possible de générer les probabilités d’appartenance a posteriori qui ont été affichés au sein du tableau « Classification » vu plus haut. Ceci donne :

Probabilité(classe 1) = 0,9196 ; Probabilité(classe 2) = 0,0787 ; Probabilité (classe 3) = 0,0017.

La formule utilisée est la suivante :

Probabilité(classe k) = exp[score(k)]/ [ exp(score1) + exp(score2) + exp(score3)] k=1,2,3.