Analyse Factorielle Discriminante AFD dans Excel

Ce tutoriel vous aidera à configurer et interpréter une Analyse Factorielle Discriminante (AFD) dans Excel avec le logiciel XLSTAT.

Jeu de données pour réaliser une Analyse Factorielle Discriminante

Les données proviennent de [Fisher M. (1936). The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7, pp 179 -188] et correspondent à 150 fleurs d'Iris, décrites par 4 variables quantitatives (longeur des sépales, largeur des sépales, longueur des pétales, largeur des pétales, et par leur espèce.

But de cette analyse discriminante

Trois différentes espèces font partie de cette étude : setosa, versicolor and virginica. Notre but est de tester si les quatre variables descriptives permettent de distinguer les espèces, puis de représenter les données dans l'espace factoriel, afin de vérifier visuellement si les espèces sont bien discriminées.

Iris setosa, versicolor et virginica.

Paramétrer une Analyse Factorielle Discriminante

• Une fois XLSTAT lancé, choisissez la commande XLSTAT / Analyse des données / Analyse Factorielle Discriminante.

• Une fois le bouton cliqué, la boîte de dialogue correspondant à l'Analyse Factorielle Discriminante (AFD) apparaît.

• Vous pouvez alors sélectionner les données sur la feuille Excel. La variable dépendante qualitative, qui correspond à la variable à modéliser, est dans ce cas précis, l'"espèce d'Iris".

• Les variables explicatives sont les quatre variables dont on dispose.

• L'option Libellés des variables est laissée activée car la première ligne des colonnes sélectionnées comprend le nom des variables.

• Dans l'onglet des options, nous avons décoché l'option Egalité des matrices de covariance intra-classes, car comme nous le verrons plus loin (test de Box), cette hypothèse n'est pas acceptable au seuil de 5%.

• Au niveau de l'onglet Graphiques, nous avons choisi de ne pas afficher les étiquettes des observations afin de ne pas alourdir les graphiques.

• Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.

Interpréter les résultats d'une Analyse Factorielle Discriminante

Après les statistiques descriptives concernant les différentes variables, XLSTAT affiche les matrices de covariance impliquées dans les calculs. Les deux tests de Box permettent de confirmer que l'on ne peut pas faire l'hypothèse que les matrices de covariance sont identiques pour les 3 espèces.

Le test du Lambda de Wilks permet de tester si les vecteurs des moyennes pour les différentes groupes sont égaux ou non (ce test peut être compris comme un équivalent multidimensionnel du test LSD de Fisher ou du test HSD de Tukey). On voit ici que la différence entre les vecteurs est significative au niveau de signification de 0.05.

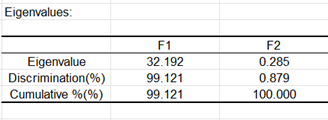
Le tableau suivant fournit les valeurs propres et le % de variance correspondant. On peut voir que 99% de la variance sont représentés par le premier facteur. Il n'y a ici que deux facteurs, ce qui n'est pas surprenant : en effet, le nombre maximum de facteurs non nuls vaut k-1, lorsque n>p>k, où n est le nombre d'observations, p le nombre de variables explicatives et k le nombre de groupes.

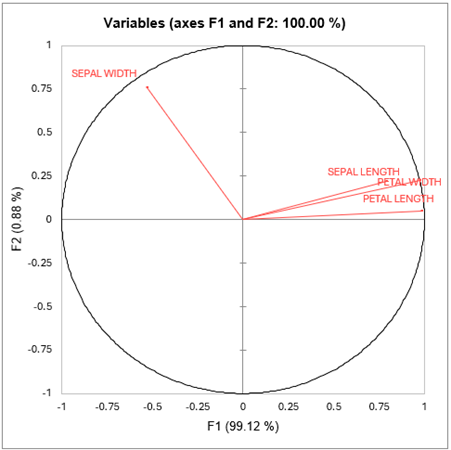
Le graphique suivant montre comment les quatre variables initiales sont corrélées avec les deux facteurs obtenus (ce graphique est contruit à partir du tableau des coordonnées des variables). On peut voir que le facteur F1 est corrélé avec Long. Sép., Long. Pét. et Larg. Pét. et que F2 est corrélé avec Larg. Pét. La longueur des pétales semble être la variable la plus discriminante.

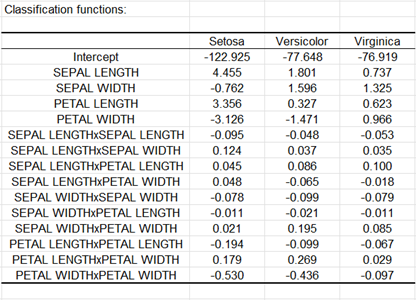
Dans le tableau suivant sont affichées les fonctions discriminantes. Lorsque l'on suppose que les matrices de covariance sont égales, ces fonctions sont linéaires. Dans le cas contraire, elles sont quadratiques, ce qui est ici le cas. La règle fondée sur ces fonctions est telle que l'on attribue un individu au groupe dont la fonction discriminante donne la valeur la plus élevée.

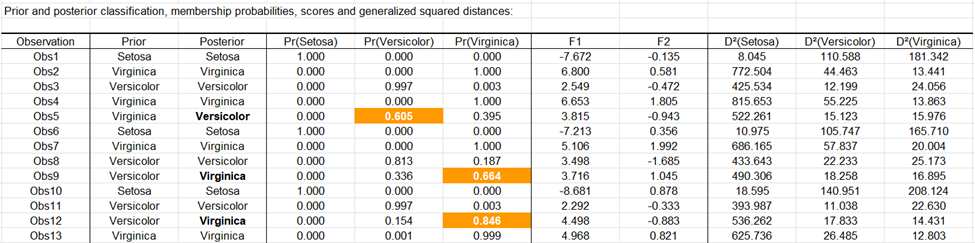
Le tableau suivant liste pour chaque fleur, ses coordonnées factorielles, la probabilité d'affectation à chacun des groupes, et le carré des distances de Mahalanobis au centroïde de chacun des groupes. Chaque observation est reclassée dans le groupe pour lequel la probabilité est maximale. Les probabilités sont des des probabilités a posteriori qui prennent en compte les probabilités a priori au travers de la formule de Bayes. On remarque que les observations (5,9,12) ont été reclassées. If peut y avoir plusieurs raisons pour cela: soit la personne qui a fait mes mesures a fait une erreur d'enregistrement, soit les iris correspondant à ces données ont eu une croissance anormale pour des raisons inconnues, soit le critère de classement utilisé par le spécialiste n'est pas correcte, soit il manque de l'information pour discriminer parfaitement les espèces entre elles.

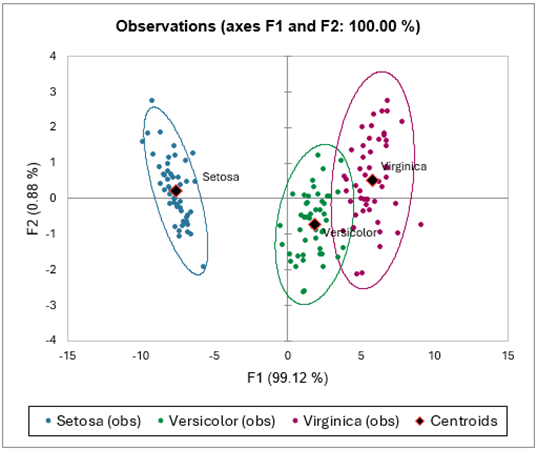
Sur le graphique suivant sont affichés les individus sur les axes factoriels. Ce graphique permet de confirmer que les individus sont bien discriminés sur les axes factoriels obtenus à partir des variables explicatives initiales. Le graphique étant bien orthonormé, on peut constater que c'est bien le premier axe qui discrimine le mieux les trois espèces. Les barycentres des trois espèces sont affichés, ainsi que les ellipses de confiance.

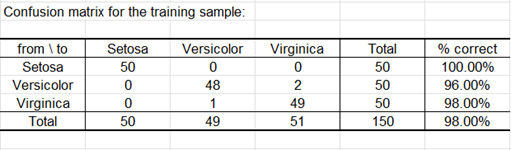
La matrice de confusion résume l'information concernant les reclassements d'observations, et on peut en déduire les taux de bon et mauvais classement. Le "% correct" correspond au rapport du nombre d'observations bien classées, sur le nombre total d'observations.

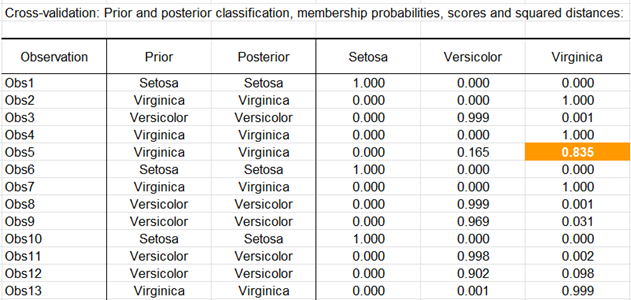
Comme l'option correspondante a été activée dans l'onglet "Résultats" de la boîte de dialogue, les prédictions pour la validation croisée sont calculées. La validation croisée permet de voir quelle serait la prédiction pour une observation donnée si elle était exclue de l'échantillon d'estimation. Nous pouvons voir ici qu'une seule observation supplémentaire (Obs5) est mal classée.

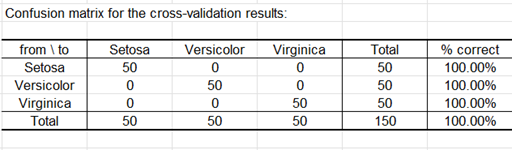
La matrice de confusion de la validation croisée est affichée ci-dessous.