Analyse factorielle dans Excel

Ce tutoriel vous aidera à configurer et interpréter une Analyse Factorielle dans Excel avec le logiciel XLSTAT. Ce guide vous permettra de choisir une méthode d'analyse multivariée appropriée en fonction de votre question et vos données.

Jeu de données pour l'analyse factorielle

Les données proviennent de [Kendall M. (1975). Multivariate analysis. Griffin, London] et correspondent à 48 candidats pour un poste en entreprise ayant été évalués sur 15 critères :

• Lettre de motivation
• Présentation
• Niveau d'études
• Sympathie
• Confiance en soi
• Lucidité
• Honnêteté
• Sens commercial
• Expérience
• Charisme
• Ambition
• Compréhension
• Potentiel
• Motivation pour le poste
• Adéquation

Parce que les corrélations entre les critères sont importantes, il est possible que la personne interviewant les candidats ait confondu certains critères ou que certains critères soient redondants. On a procédé à une analyse factorielle, afin de déterminer quels sont les critères (ou facteurs) latents.

Plusieurs méthodes d'analyse factorielle existent. Trois méthodes d'extraction des facteurs sont proposées par XLSTAT (composantes principales, facteurs principaux, et maximum de vraisemblance).

Nous utilisons ici la méthode des facteurs principaux dans le but de générer quatre facteurs, avant de procéder à une rotation varimax pour faciliter l'interprétation des résultats.

Paramétrer une analyse factorielle

Pour activer la boîte de dialogue de l'analyse factorielle, lancez XLSTAT, puis sélectionnez la commande XLSTAT / Analyse de données / Analyse Factorielle.

Une fois le bouton cliqué, la boîte de dialogue apparaît. Vous pouvez alors sélectionner les données sur la feuille Excel.

Dans l'onglet Options la rotation Varimax sur les deux premiers facteurs a été choisie.

Les options de sorties et de graphiques suivantes sont activées.

Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.

Interpréter les résultats d'une analyse factorielle

Les premiers résultats sont les statistiques descriptives simples des variables sélectionnées, puis la matrice de corrélation pour ces mêmes variables. On note que certaines corrélations sont importantes (0.883 pour Compréhension et Lucidité). On remarque que le juge est probablement influencé par l'expérience et le charisme du candidat lorsqu'il détermine l'Adéquation entre le candidat et le poste.

Le alpha de Cronbach standardisé est ensuite calculé. Il vaut ici 0.914, ce qui indique qu'il y a probablement de la redondance dans les variables sélectionnées.

L'agorithme utilisé pour le calculs des facteurs principaux est itératif. Dans notre cas, l'algorithme a convergé au bout de 41 itérations pour atteindre une précision de 0,0001 sur le critère du changement maximum de communalité entre deux itérations. La méthode consiste à essayer de reproduire la matrice des corrélations. La matrice des corrélations reproduites et des corrélations résiduelles permet de mesurer cas par cas si les corrélations sont bien reproduites ou non.

Dans le tableau ci-dessous sont affichées les valeurs propres issues de l'analyse factorielle. Nous constatons qu'avec quatre facteurs on conserve 74.5 % de la variabilité des données initiales.

Remarque : les valeurs propres affichées ci-dessus sont celles qui correspondent à l'analyse factorielle par la méthode des facteurs prinicpaux. Avec l'analyse en composantes principales on obtiendrait pour les 10 premiers facteurs :

La rotation varimax change la façon dont chaque facteur représente une part de la variance. La rotation varimax rend l'interprétation plus aisée en maximisant la variance du carré des coordonnées des variables par colonne. Pour un facteur donné, les coordonnées élevées le sont encore plus, les coordonnées faibles le sont encore plus, et les coordonnées intermédiaires deviennent soit plus élevées, soit plus faibles. Le % de variance correspondant au premier reste bien entendu inchangé, même si au niveau de chacun des deux axes pris en compte pour la rotation les % sont inchangés.

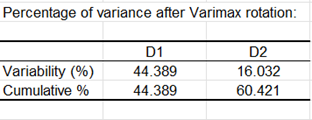
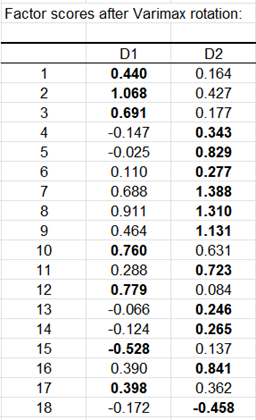
On peut ensuite analyser les coordonnées des variables après la rotation varimax. Ces résultats sont utilisés pour interpréter le sens des facteurs après rotation.

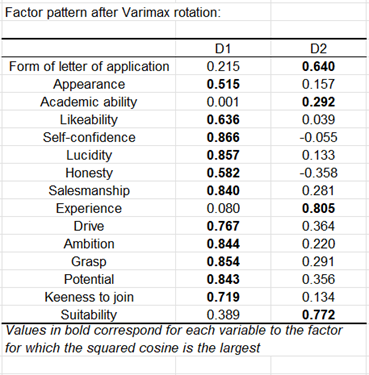
D'après le tableau ci-dessus, on remarque que le premier facteur est fortement lié à l'Ambition, à la Confiance en soi, au Sens commercial et à la Lucidité. Le second facteur est quant à lui lié à la Lettre de motivation, à l'Expérience, et à l'Adéquation. De ces résultats, on déduit que les candidats qui ont des coordonnées élevées sur le premier facteur sont des commerciaux prometteurs, tandis que ce que l'on destinerait à des postes de management auraient plutôt des coordonnées élevées sur le second et le troisième facteurs.

Le graphique ci-dessous donne la position des variables sur les axes F1 et F2.

Le alpha de Cronbach est ensuite calculé pour chaque facteur, en prenant pour chaque facteur, les variables dont la valeur absolue de la coordonnée (ou loading) est maximale pour ce facteur. Le alpha est proche de 1 pour les facteurs après rotation. Ceci semble confirmer que ces deux facteurs ont un caractère unidimensionnel, traduisant un facteur latent.

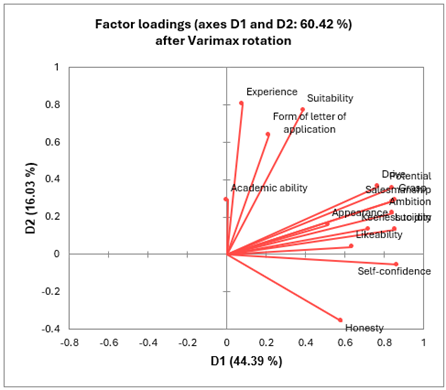
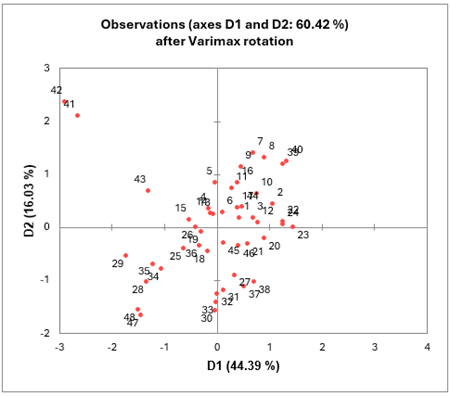
Un tableau suivant fournit les coordonnées des individus sur les axes factoriels après la rotation varimax.

XLSTAT affiche la carte factorielle en deux dimensions. Le graphique ci-dessous correspond à la carte factorielle sur F1 et F2.

Les meilleurs candidats sont probablement les individus 40 et 39. S'ils refusent l'offre, les candidats 8, 20,22,23,24 seraient une alternative.

La vidéo suivante aborde l'Analyse Factorielle, avec une illustration sur XLSTAT.