Faktoranalysen (FA) in Excel - Anleitung

Dieses Tutorium wird Ihnen helfen, eine Faktorenanalyse (FA) in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.

Datensatz für die Durchführung einer Faktorenanalyse

Die Daten stammen aus [Kendall M. (1975). Multivariate analysis. Griffin, London] und entsprechen 48 Bewerbern für eine Stelle in einem Unternehmen, die bezüglich der 15 folgenden Merkmale bewertet wurden:

• Bewerbungsbrief

• Präsentation

• Schul und Studienabschluss

• Sympathie

• Selbstsicherheit

• Auffassungsgabe

• Ehrlichkeit

• Verkaufssinn

• Berufserfahrung

• Charisma

• Ehrgeiz

• Verständnis

• Potential

• Motivation für die Stelle

• Eignung

Ziel dieses Tutorials

Aufgrund der vielen hohen Korrelationen zwischen den Variablen wurde angenommen, dass der Richter einige Variablen verwechseln könnte oder dass einige Variablen redundant sein könnten. Wir werden die Hauptfaktormethode iterativ anwenden, um die wenigen zugrunde liegenden Faktoren zu bestimmen, und eine Varimax-Rotation durchführen, um die Interpretation der Ergebnisse zu erleichtern.

Einrichten einer Faktorenanalyse

• Starten Sie XLSTAT und wählen den Befehl XLSTAT/Analyse der Daten/Faktorenanalyse.

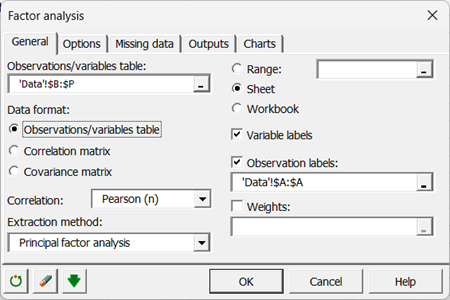
• Nach dem Klicken des Button erscheint das Dialogfenster. Sie können nun die Daten auf dem Excel-Blatt auswählen.

• Die Beobachtungsbeschriftungen werden ebenfalls im entsprechenden Feld ausgewählt.

• Im Reiter Optionen wählen Sie die Rotation Varimax auf die beiden ersten Faktoren.

• Nach dem Klicken auf den Button OK, beginnen die Berechnungen und die Ergebnisse werden angezeigt.

Interpretieren der Ergebnisse einer Faktorenanalyse

Die ersten Ergebnisse sind die beschreibenden einfachen Statistiken der ausgewählten Variablen, dann eine Korrelationsmatrix für dieselben Variablen. Man bemerkt, dass einige Korrelationen hohe Werte aufweisen (0,883 für Verständnis und Auffassungsgabe). Man bemerkt, dass der Beurteiler vielleicht durch die Berufserfahrung und das Charisma des Bewerbers beeinflusst ist, wenn er die Eignung für die Stelle beurteilt.

Das standardisierte Alpha von Cronbach wird im Anschluss berechnet. Hier hat es einen Wert von 0,914, was darauf hindeutet, dass es sehr wahrscheinlich Redundanz in den ausgewählten Variablen gibt.

Der zur Berechnung der Hauptfaktoren verwendete Algorithmus ist iterativ. In unserem Fall konvergiert der Algorithmus nach 41 Iterationen um eine Genauigkeit von 0,0001 in Bezug auf das Kriterium der Veränderung des Maximums der Kommunalitäten zwischen zwei Iterationen. Die Matrix der reproduzierten Korrelationen und die Residualkorrelationen erlauben es von Fall zu Fall zu entscheiden, ob die Korrelationen gut oder schlecht reproduziert wurden.

In der unten abgebildeten Tabelle werden die Eigenwerte aus der Faktorenanalyse angezeigt. Man stellt fest, dass mit vier Faktoren 75,5 % der Variabilität der Ausgangsdaten erhalten werden.

Bemerkung: Die oben angezeigten Eigenwerte entsprechen denen der Faktorenanalyse mittels Hauptfaktoren.

Im Fall einer Analyse mit Hauptkomponenten erhält man die folgenden 10 ersten Faktoren:

Die Varimax-Rotation verändert die Art und Weise, auf die jeder Faktor einen Anteil der Varianz darstellt. Die Varimax-Rotation erleichtert die Interpretation, indem Sie die Varianz der Quadrate der Koordinaten der Variablen pro Spalte maximiert. Für einen gegebenen Faktor bewirkt dies, dass die hohen Koordinaten noch höher werden, die kleinen Koordinaten noch geringer und die mittleren Koordinaten werden entweder zu hohen oder kleinen Koordinaten.

Der Prozentsatz der Varianz, die dem ersten Faktor entspricht bleibt unverändert, ebenso wie in Bezug auf die beiden ersten für die Rotation betrachteten Achsen die Prozentsätze unverändert sind.

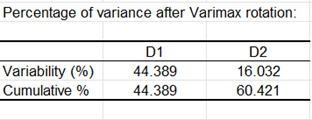
Man kann im Anschluss die Koordinaten der Variablen nach der Varimax-Rotation analysieren. Diese Ergebnisse sind nützlich zur Interpretation des Sinns der Faktoren nach der Rotation.

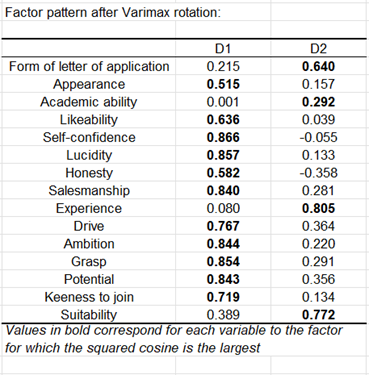
Gemäß der oben abgebildeten Tabelle bemerkt man, dass der erste Faktor stark mit dem Ehrgeiz, der Selbstsicherheit, dem Verkaufssinn und der Auffassungsgabe verbunden sind.

Der zweite Faktor ist seinerseits mit dem Bewerbungsbrief, der Berufserfahrung und der Eignung verbunden. Aus diesen Ergebnissen kann man schließen, dass die Bewerber mit hohen Koordinaten für den ersten Faktor Erfolg versprechende Vertriebler sind, wogegen man für Managementstellen eher Bewerber mit hohen Koordinaten für den zweiten und dritten Faktor vorschlägt.

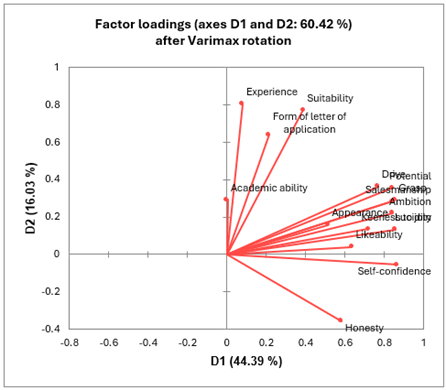
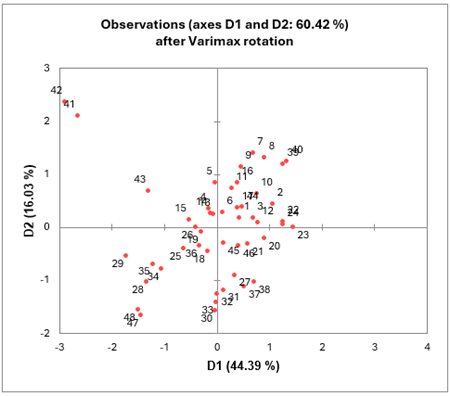
Das unten abgebildete Diagramm gibt die Position der Variablen in Bezug auf die Achsen F1 und F2 an.

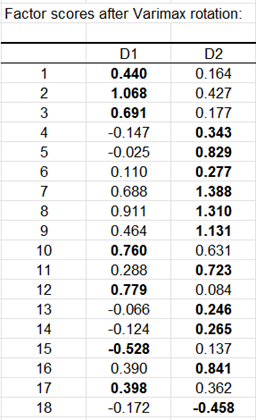
Die folgende Tabelle gibt die Koordinaten der Individuen für die Faktorachsen nach der Varimax-Rotation an.

XLSTAT zeigt eine Faktorenkarte in zwei Dimensionen an. Das unten abgebildete Diagramm entspricht der Karte der Faktoren F1 und F2.

Das folgende Video behandelt die Faktorenanalyse mit einer Veranschaulichung unter Verwendung von XLSTAT.