Korrespondenzanalyse (KA) in Excel - Anleitung
Dieses Tutorium wird Ihnen helfen, eine Korrespondenzanalyse (KA) in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.
Sie sind nicht sicher, ob dies das richtige Tool für die multivariate Datenanalyse ist, das Sie benötigen? Weitere Hinweise finden Sie hier.
Datensatz für die Durchführung einer Korrespondenzanalyse
Die Daten entsprechen einer Umfrage, bei der Kinogänger zu ihrer Meinung über einen Film befragt wurden, den sie soeben angeschaut hatten. Die Zuschauer wurden auch gebeten, ihre Alterskategorie anzugeben.
Ziel dieses Tutorials
Ziel dieses Tutorials ist es, zu lernen, wie man eine Korrespondenzanalyse einrichtet und interpretiert. Die Ziele dieser Methode sind, die Assoziation zwischen zwei Variablen (Zeilen und Spalten einer Kreuztabelle) und die Ähnlichkeiten zwischen den Kategorien jeder Variablen (Zeilen und Spalten) zu untersuchen.
Erstellen einer Korrespondenzanalyse
-
Nach dem Öffnen von XLSTAT wählen Sie den Befehl XLSTAT/Analyse der Daten/Korrespondenzanalyse.
-
Nach dem Klicken des entsprechenden Buttons erscheint das Dialogfenster Korrespondenzanalyse.
-
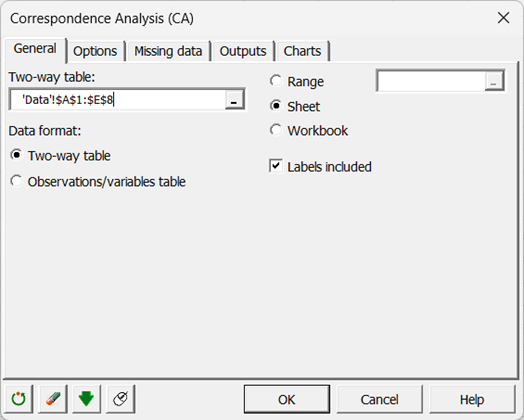
Markieren Sie die Daten in dem Excel-Tabellenblatt. Falls Ihre Daten in Form einer Kreuztabelle vorliegen (wie im Beispiel unten), wählen Sie das Format Kreuztabelle. Falls Ihre Daten im Format Beobachtungen/Variablen erfasst wurden, wählen Sie die entsprechende Option.
-
Falls die Kategorienamen der Kontingenztabelle eingeschlossen wurden, wählen Sie die Option Beschriftungen eingeschlossen.
-
Auf der Registerkarte Optionen wählen Sie Keine für die Option Fortgeschrittene Analyse.
-
Wählen Sie nicht die Option Nicht-symmetrische Analyse und wählen Sie Chi-Quadrat für den Abstand. Diese Kombination aus Optionen ermöglicht die Berechnung der klassischen Korrespondenzanalyse (KA).
Hinweis: Um eine nicht-symmetrische Korrespondenzanalyse (NSKA) auszuführen, würden Sie die Option Nicht-symmetrische Analyse wählen (für die nur der Chi-Quadrat-Abstand verfügbar ist).
Um eine Korrespondenzanalyse basierend auf dem Hellinger-Abstand (HA) durchzuführen, würden Sie nicht die Option Nicht-symmetrische Analyse sondern Hellinger für den Abstand wählen.
-
Im Tab „Ausgaben“ wählen Sie die Zeilen- und Spaltenprofile sowie die Chi-Quadrat-Distanz aus.
-
In der Unterregisterkarte Karten der Registerkarte Diagramme stehen drei alternative Möglichkeiten zur Darstellung der Ergebnisse zur Verfügung. Das symmetrische Zeilen- und Spaltendiagramm wird am häufigsten verwendet. Zum Zwecke des Tutoriums wurden alle Darstellungsalternativen ausgewählt.
-
In der Unterregisterkarte Zeilenoptionen und Spaltenoptionen der Registerkarte Diagramme wählen Sie die Option Konfidenz-Ellipsen aus.
-
Klicken Sie auf den Button OK. Es erscheint ein Dialogfenster, in dem Sie die Achsen auswählen, die Sie auf der grafischen Darstellung der Korrespondenzanalyse (F1 und F2 in diesem Tutorium) anzeigen und bestätigen.
Interpretation der Korrespondenzanalyse
Bevor wir mit der Interpretation beginnen, lassen Sie uns zunächst das Profilkonzept vorstellen. Die Korrespondenzanalyse basiert in der Tat auf der Analyse der Profile. Ein Profil ist eine Menge von Häufigkeiten dividiert durch ihre Gesamtsumme, d. h. relative Häufigkeiten. Anders gesagt spiegelt ein Profil wider wie sich die Kategorie einer Variablen entsprechend den Kategorien der anderen Variablen ändert.
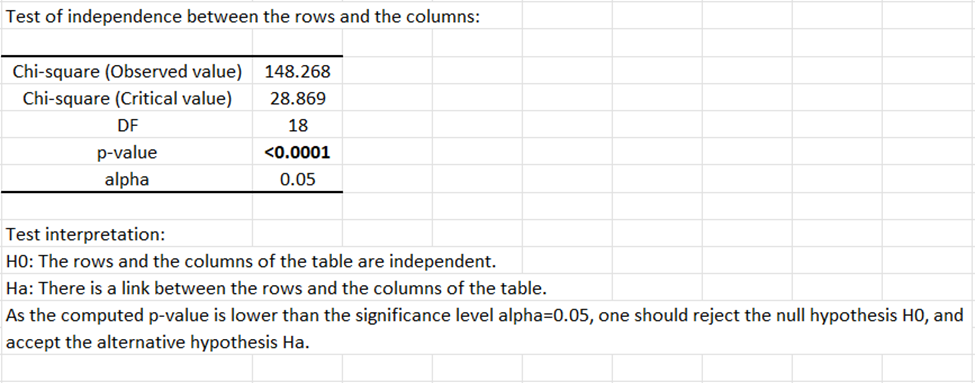
Das erste angezeigte Ergebnis ist der Unabhängigkeitstest zwischen Zeilen und Spalten basierend auf einer Chi-Quadrat-Statistik. Wenn das beobachtete Chi-Quadrat größer ist als der kritische Wert, dann liegt der p-Wert unter dem ausgewählten alpha-Niveau, und man kann schlussfolgern, dass die Zeilen und Spalten der Tabelle signifikant zusammenhängen. In unserem Beispiel ist es sehr wahrscheinlich, dass reale Unterschiede zwischen den Altersgruppen hinsichtlich ihrer Beurteilungsprofile bestehen.
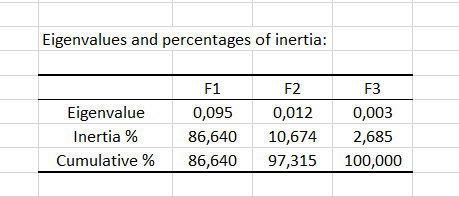
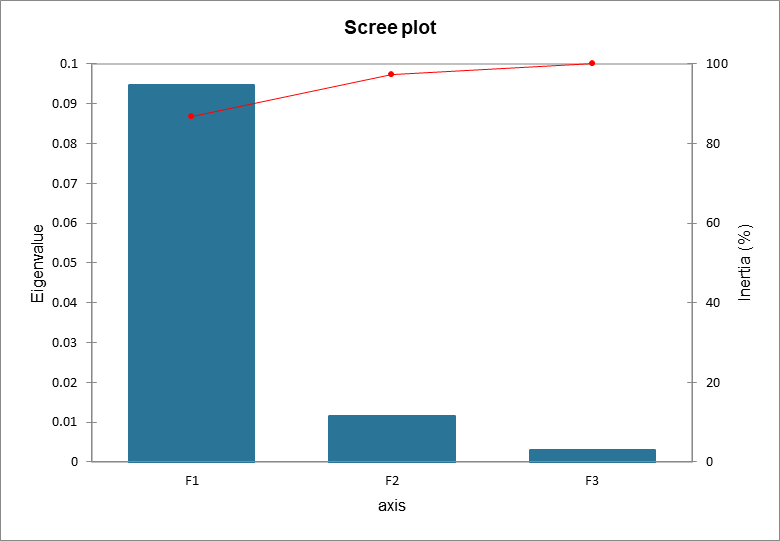
Die Eigenwerte entsprechen der Varianz extrahiert nach jedem Faktor (Dimension). Die Qualität der Analyse kann durch Betrachten der Tabelle der Eigenwerte oder des entsprechenden Scree plot bewertet werden. Falls die Summe der zwei ersten (oder der ersten wenigen) Eigenwerte nahe am dargestellten Gesamtanteil liegt, so ist die Qualität der Analyse sehr hoch. Die Korrespondenzanalyse im vorliegenden Beispiel weist eine gute Qualität auf, weil die Summe der beiden ersten Eigenwerte zusammen 97 % der Gesamtträgheit ausmachen.
Eine Liste der Tabellen wird dann für die Zeilen (bzw. Spalten) angezeigt.
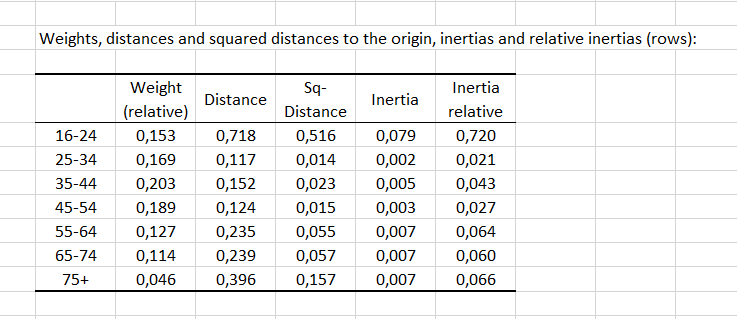
Eine erste Tabelle zeigt die Gewichte, Abstände und quadratischen Abstände vom Ursprung, Trägheiten und relative Trägheiten der Zeilen (bzw. Spalten). Die Gewichte sind nebensächliche Verhältnisse, die zum Gewichten der Punktprofile beim Berechnen der Abstände verwendet werden. Je größer der Abstand zum Ursprung, desto größer ist die Unähnlichkeit zwischen dem Kategorieprofil und dem Mittelwertprofil (desto mehr trägt die Kategorie zur Abhängigkeit zwischen den beiden Variablen bei). Die Altersgruppen 25-34, 35-44 und 45-54 haben den geringsten Abstand zum Ursprung, was zeigt, dass diese Gruppenprofile nahe am Mittelwertprofil liegen.
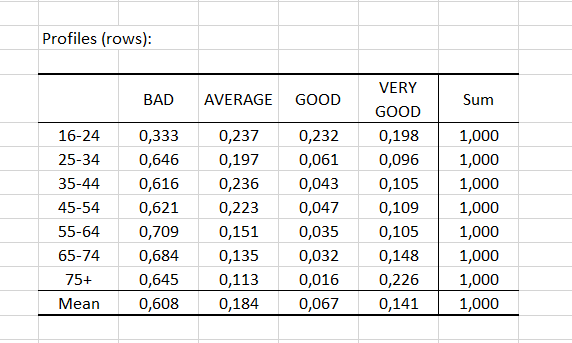
Die Zeilen-(bzw. Spalten)-Profile werden dann ebenso wie das Mittelwertprofil angezeigt. In unserem Beispiel liegen die Profile der Altersgruppen 25-34, 35-44 und 45-54 eng beieinander und nahe am Mittelwertprofil. Letzteres war durch den geringen Abstand zum Ursprung vorherzusehen.
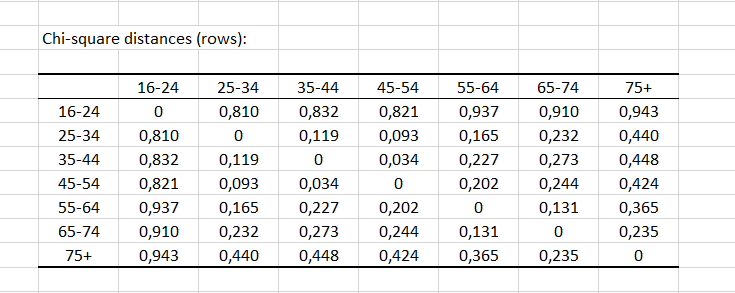
Die Abstände zwischen den Zeilen (bzw. Spalten) geben uns Informationen über die Ähnlichkeit zwischen Kategorien. Wiederum scheinen die Altersgruppen 35-34, 35-44 und 45-54 ähnlich zu sein und einen Abstand von weniger als 0,2 aufzuweisen.
Dann werden die Tabellen der Hauptkoordinaten und Standardkoordinaten der Zeilen (bzw. Spalten) angezeigt. Die Standardkoordinaten sind Hauptkoordinaten dividiert durch die Quadratwurzel des entsprechenden Faktor-Eigenwerts. Die gewichtete Summe der Quadratwerte der Standardkoordinaten ergibt für jeden Faktor 1.
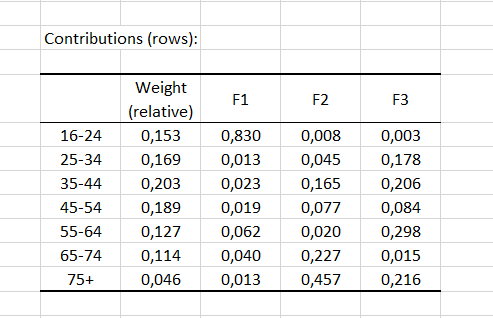
Nachstehend finden Sie eine Tabelle der Beiträge der Zeilen (bzw. Spalten). Die Beiträge entsprechen der Wichtigkeit jeder Kategorie für jeden Faktor (Dimension). Die Summe der Beiträge ergibt für jeden Faktor 1. Als Faustregel gilt: Wenn der Beitrag größer ist als 1/I, wobei I die Anzahl der Zeilen (bzw. 1/J, wobei J die Anzahl der Spalten) ist, ist die Kategorie für den gegebenen Faktor von Bedeutung. In unserem Beispiel ist die Gruppe 16-24 von Bedeutung für Faktor F1, und die Gruppen 65-74 und 75+ sind von Bedeutung für Faktor F2.
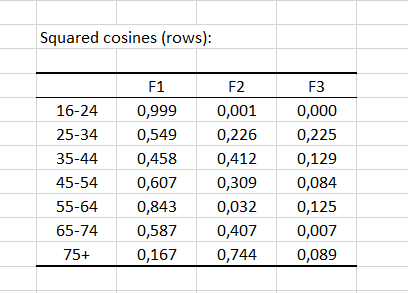
Die nächste Tabelle zeigt die quadrierten Cosinuswerte der Zeilen (bzw. Spalten). Die quadrierten Cosinuswerte entsprechen der Wichtigkeit jedes Faktors für jede Kategorie. Die Summe der quadrierten Cosinuswerte ergibt für eine gegebene Kategorie 1. In unserem Beispiel wird fast die gesamte Varianz der Gruppe 16-24 dem Faktor 1 zugeordnet.
Dann werden die verschiedenen Diagramme angezeigt.
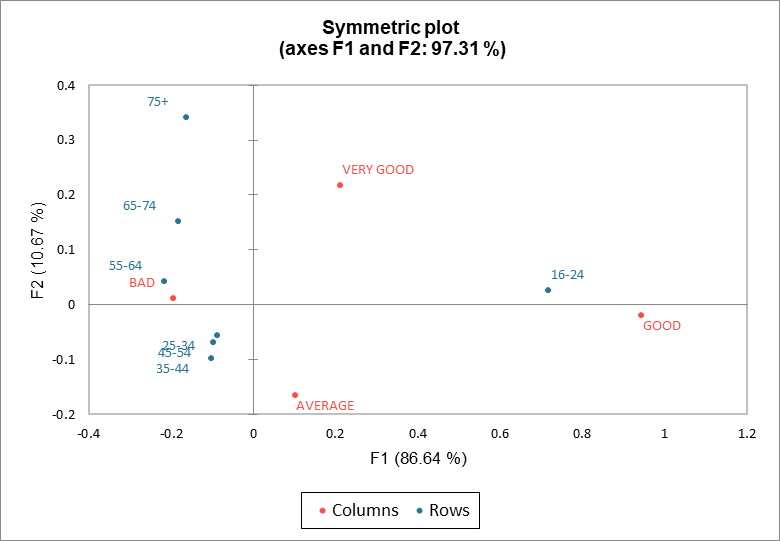
Das symmetrische Diagramm oder Französische Diagramm wird am häufigsten verwendet. Die Zeilenprofile und Spaltenprofile überlagern sich in einer gemeinsamen Darstellung (beide in Hauptkoordinaten). Diese Darstellung ist sehr praktisch, da sowohl Zeilen- als auch Spaltenpunkte gleich verteilt sind. Der Abstand zwischen den Zeilenpunkten (bzw. Spaltenpunkten) entspricht in etwa dem Chi-Quadrat Abstand zwischen den Zeilen- (bzw. Spalten). Die Altersgruppen 25-34, 35-44 und 45-54 überlagern sich beinahe im symmetrischen Diagramm und zeigen sehr ähnliche Profile.
Der Abstand zwischen den Zeilen- und Spaltenpunkten kann nicht direkt interpretiert werden.
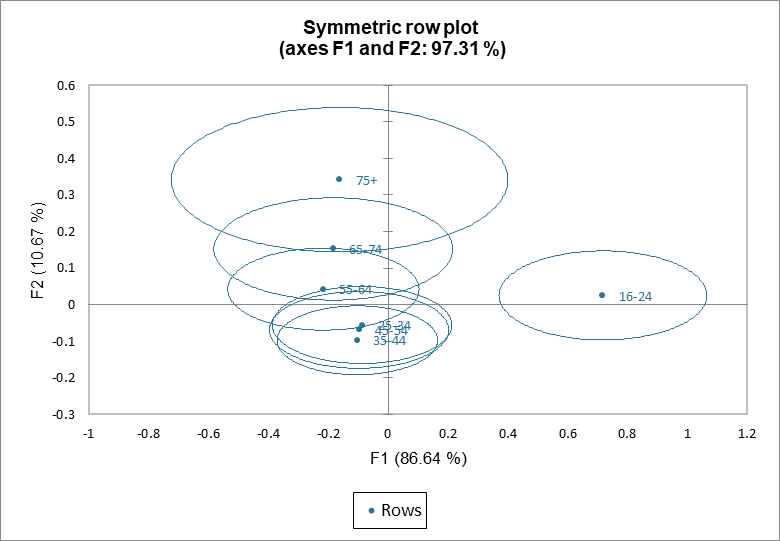
Konfidenz-Ellipsen können zu den symmetrischen Diagrammen hinzugefügt werden, wie im symmetrischen Diagramm der Zeilen zu sehen. Wenn der Ursprung in der Ellipse einer gegebenen Kategorie liegt, trägt diese Kategorie nicht zur Abhängigkeit zwischen Variablen bei. In unserem Beispiel bestätigen die Ellipsen, dass die Altersgruppen 25-34, 34-45 und 45-54 nicht zur Abhängigkeit zwischen den Variablen beitragen. Die Altersgruppe 16-24 trägt zur Abhängigkeit zwischen den Variablen bei.
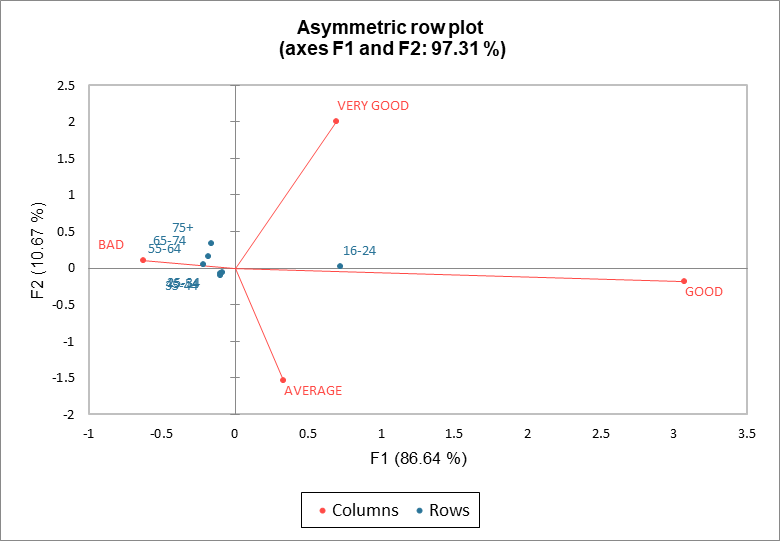
Das asymmetrisches Diagramm der Zeilen zeigt die Spalten, die im Zeilenraum dargestellt werden (Spalten von den Standardkoordinaten und Zeilen von den Hauptkoordinaten). Umgekehrt entspricht das asymmetrisches Diagramm der Spalten den im Spaltenraum dargestellten Zeilen. Der Abstand zwischen Zeilen und Spalten muss durch Projizieren der Zeilenpunkte auf die Spaltenvektoren interpretiert werden. Ob die Achsen in Bezug auf Zeilen oder Spalten zu interpretieren sind, hängt davon ab, wie angemessen die Interpretation ist. In unserem Beispiel interpretieren wir die Altersgruppe im Beurteilungsbereich. Die erste Dimension ist eine Gegenüberstellung von gut und schlecht. In der Altersgruppe 16-24 wurde das Produkt durch einen höheren Anteil als gut bewertet, im Gegensatz zu den Anteilen von „gut“ in anderen Altersgruppen. Das bedeutet allerdings nicht, dass die Bewertung „gut“ den höchsten Anteil im Vergleich zu den anderen Bewertungen in der Altersgruppe 16-24 hat. Die Zeilenprofile weichen nicht wesentlich vom Mittelwertprofil ab (Zeilenpunkte liegen nahe am Ursprung).
Die Beitragskoordinaten der Zeilen und Spalten werden dann angezeigt. Die Beitragskoordinaten erhält man durch Dividieren der Standardkoordinaten durch die Quadratwurzel der Masse der gegebenen Kategorie.
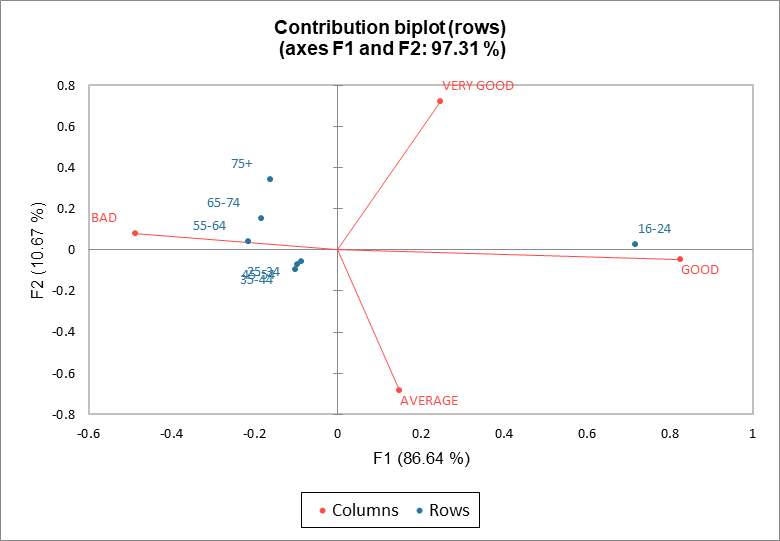
Im Beitragsbiplot (Zeilen) sind die Zeilen in Beitragskoordinaten und die Spalten in Hauptkoordinaten und umgekehrt für den Beitragsbiplot (Spalten) dargestellt. Im Beitragsbiplot der Zeile (bzw. der Spalte) beziehen sich die Abstände der Zeilenpunkte (bzw. Spaltenpunkte) zum Ursprung auf ihren Beitrag zu der Darstellung. In unserem Beispiel ist die Position der Zeilenpunkte im Zeilenbeitragsbiplot im Vergleich zum asymmetrischen Diagramm unverändert. Jedoch sind die Spaltenpunkte näher am Ursprung (siehe die Skalen der beiden Darstellungen).
Die Korrespondenzanalyse ist eine sehr effiziente Methode zur Analyse von Kreuztabellen. Wenn bei einer Umfrage mehr als zwei kategorische Variablen verwendet werden, ist die beste Methode die Verwendung der multiplen Korrespondenzanalyse (MKA).
Das folgende Video behandelt die Theorie der Korrespondenzanalyse (CA) und deren Implementierung in XLSTAT.
War dieser Artikel nützlich?
- Ja
- Nein
