Analyse Factorielle des Correspondances (AFC) dans Excel

Ce tutoriel vous aidera à configurer et interpréter une Analyse Factorielle des Correspondances (AFC) dans Excel avec le logiciel XLSTAT.

Ce guide vous permettra de choisir une méthode d'analyse multivariée appropriée en fonction de votre question et vos données.

Jeu de données pour réaliser une Analyse Factorielle des Correspondances

Les données correspondent à une enquête dans laquelle les personnes interrogées donnent leurs opinions sur un film qu'elles viennent de voir. On leur demande également leur tranche d'âge.

But de ce tutoriel

Le but de ce tutoriel est d’apprendre à mettre en place et à interpréter une Analyse Factorielle des Correspondances. Les objectifs de cette méthode sont d'étudier l'association entre deux variables (lignes et colonnes d'un tableau de contingence) et les similitudes entre les catégories de chaque variable respectivement (lignes et colonnes respectivement).

Paramétrer une Analyse Factorielle des Correspondances dans XLSTAT

• Une fois que XLSTAT est ouvert, choisissez XLSTAT/Analyse des données/Analyse Factorielle des Correspondances.

• Une fois le bouton cliqué, la boîte de dialogue de l'Analyse Factorielle des Correspondances apparaît.

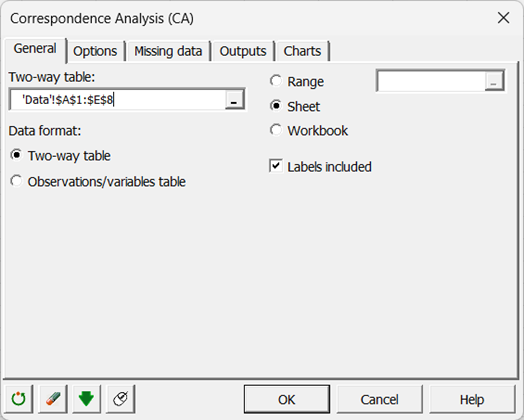
• Dans l’onglet Général, sélectionnez l’ensemble du tableau de la feuille Excel. Si vos données sont comme ici dans un tableau de contingence, sélectionnez le format Tableau croisé. Si vos données sont dans un tableau Individus/variables sélectionnez l'option Tableau observations/variables.

• Comme le nom des catégories de chaque variable est présent pour les lignes et pour les colonnes, assurez-vous que la case Libellés inclus est cochée.

Dans l'onglet Options, activez les options suivantes :

• Analyse approfondie : sélectionnez Aucune pour effectuer une AFC classique ;

• Distance : choisissez la distance Khi².

Remarques :Pour réaliser une Analyse Non Symétrique des Correspondances (ANSC), activez l'option Analyse non symétrique (pour laquelle seule la distance du Khi² est proposée).Pour réaliser une Analyse des Correspondance basée sur la distance de Hellinger (HD), n’activez pas l'option Analyse non symétrique et choisissez Hellinger pour la Distance.Pour réaliser une Analyse des Correspondances Détendancée (ACD), sélectionnez Analyse détendancée pour l’option Analyse approfondie.

• Dans l'onglet Sorties, sélectionnez les Profils de lignes et de colonnes ainsi que la distance du Chi-carré.

• Dans le sous-onglet Cartes de l'onglet Graphiques, trois possibilités de représenter les résultats sont proposées. Le graphique symétrique des lignes et colonnes est le plus couramment utilisé. Pour ce tutoriel, toutes les alternatives de cartographie ont été choisies.

• Sélectionnez en plus les Ellipses de confiance pour afficher les ellipses de confiance qui permettent d’identifier les catégories qui contribuent à la dépendance entre les variables.

• Les calculs démarrent lorsque vous cliquez sur OK. Les résultats sont ensuite affichés.

Interpréter les résultats de l’Analyse Factorielle des Correspondances

Avant de commencer l'interprétation, il est utile d’introduire le concept de profil. En effet, l'Analyse Factorielle des Correspondances est basée sur l'analyse des profils. Un profil est l’ensemble des fréquences divisées par leur total, c’est à dire les fréquences relatives. En d'autres termes, un profil reflète la façon dont la catégorie d'une variable varie selon les catégories de l'autre variable.

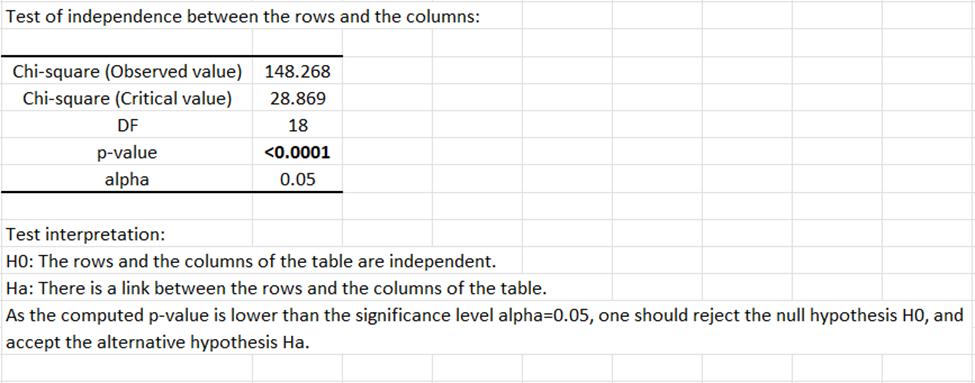
Le premier résultat affiché est le test d'indépendance entre les lignes et les colonnes, basé sur une statistique du Khi². Si la valeur du Khi² observée est supérieure à la valeur critique et si la p-value est inférieure au niveau alpha choisi, alors on peut conclure que les lignes et les colonnes du tableau de contingence sont liées de manière significative. Dans notre exemple, il est fortement probable que des différences réelles existent entre les profils d’appréciation du film et les différents groupes d'âge.

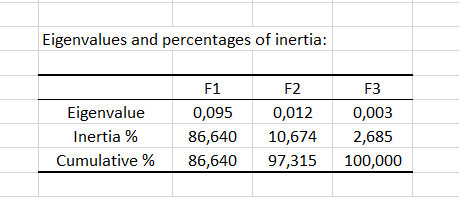
Les valeurs propres correspondent à la variance extraite par chaque facteur (dimension). La qualité de l'analyse peut être évaluée en consultant le tableau des valeurs propres ou le plot correspondant. Si la somme des deux (ou quelques) premières valeurs propres est proche de la variance totale représentée, alors la qualité de l'analyse est très bonne. Dans notre exemple, la somme des deux premières valeurs propres représente 97% de l'inertie totale, l’analyse est donc de bonne qualité.

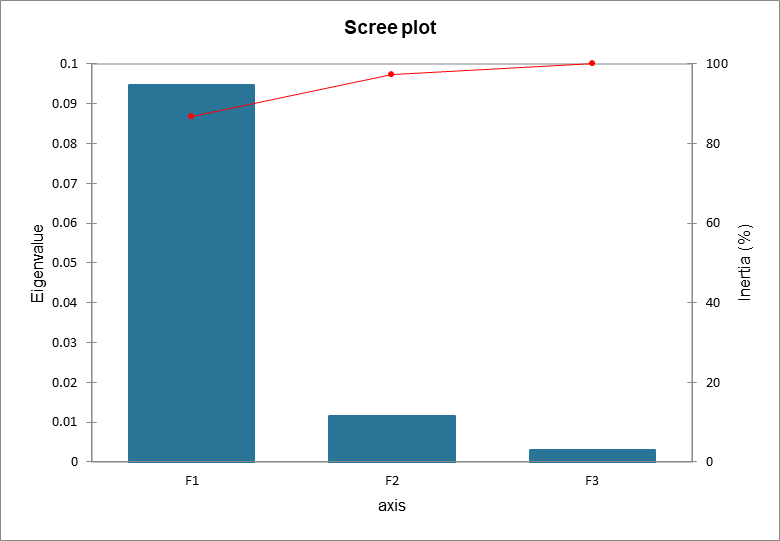
Une série de tableaux est ensuite affichée pour les lignes (et les colonnes respectivement).

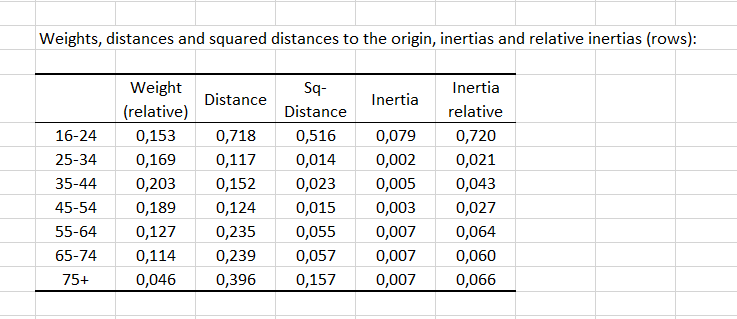
Un premier tableau contient les poids, les distances et distances quadratiques à l'origine, les inerties et inerties relatives des lignes (et respectivement des colonnes). Les poids sont des proportions marginales utilisées pour pondérer les profils des points lors du calcul des distances. Plus la distance à l'origine est grande, plus le profil de la catégorie est différent du profil moyen (plus la catégorie participe à la dépendance entre les deux variables). Les groupes d'âge 25-34, 35-44 et 45-54 ont la distance la plus courte à l'origine, ce qui indique que les profils de ces groupes sont proches du profil moyen.

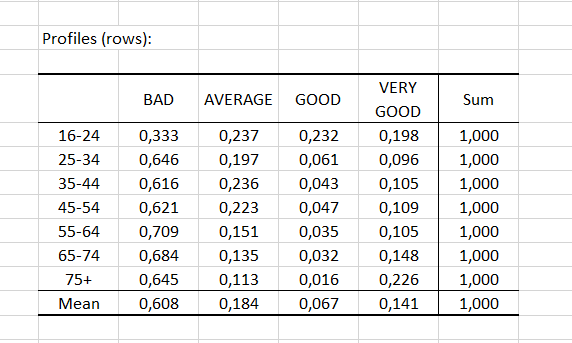
Les profils lignes (respectivement colonnes) sont ensuite affichés ainsi que le profil moyen. Dans notre exemple, les profils des groupes d'âge 25-34, 35-44 et 45-54 sont proches les uns des autres et du profil moyen. Ce dernier résultat confirme l’observation faite en analysant les distances à l’origine.

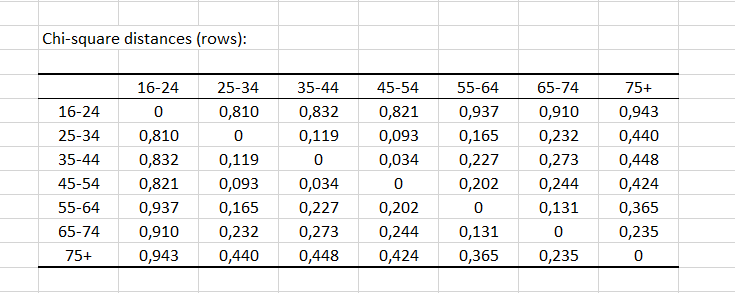
Les distances entre les lignes (respectivement colonnes) fournissent des informations sur la similitude entre les catégories. Encore une fois, les groupes d'âge 25-34, 35-44 et 45-54 semblent être similaires avec des distances inférieures à 0,2.

Les coordonnées principales et coordonnées standard des lignes (respectivement colonnes) sont ensuite affichées. Les coordonnées standard sont le résultat de la division des coordonnées principales par la racine carrée de la valeur propre du facteur correspondant. La somme des carrés pondérée des coordonnées standard est égale à 1 pour chaque facteur.

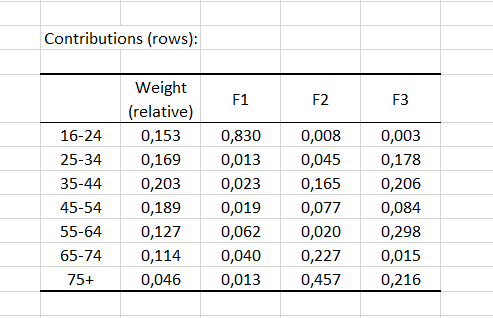
Les contributions des lignes (respectivement colonnes) sont ensuite affichées. Les contributions correspondent à l'importance de chaque catégorie pour chaque facteur (dimension). La somme des contributions est égale à 1 pour chaque facteur. En général, si la contribution est supérieure à 1/I avec I le nombre de lignes (respectivement 1/J avec J le nombre de colonnes), la catégorie est importante pour le facteur donné. Dans notre exemple, le groupe des 16-24 ans est important pour le facteur F1, les groupes des 65-74 ans et 75 ans et plus sont importants pour le facteur F2.

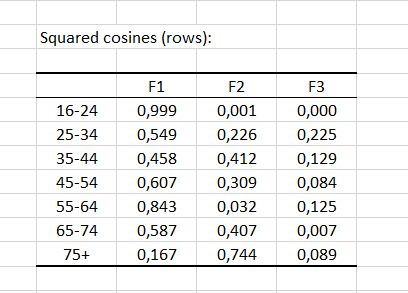
Le tableau suivant contient les cosinus carrés des lignes (respectivement colonnes). Les cosinus carrés représentent l'importance de chaque facteur pour chaque catégorie. La somme des cosinus carrés est égale à 1 pour chaque catégorie. Dans notre exemple, la quasi-totalité de la variance du groupe des 16-24 ans est attribuée au facteur F1.

Les différents graphiques sont ensuite affichés.

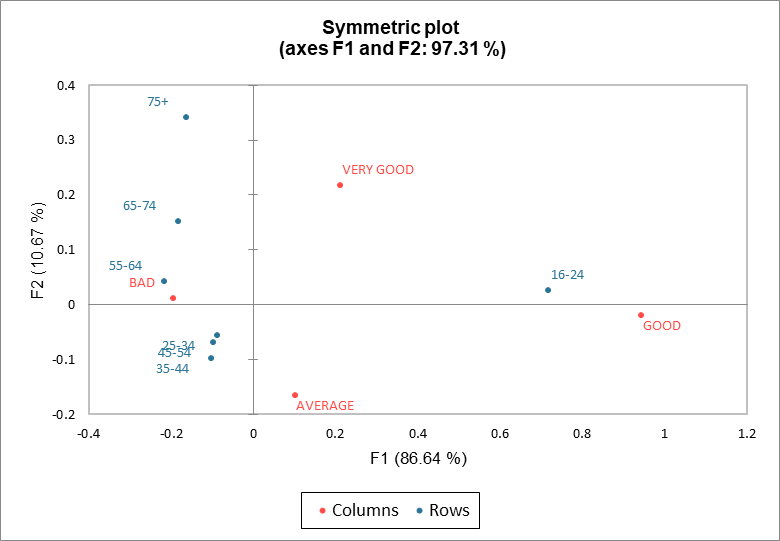
Le graphique symétrique des lignes et colonnes est le plus couramment utilisé. Les profils des lignes et des colonnes sont superposés dans un même espace (en coordonnées principales). Les points correspondants aux lignes et aux colonnes étant également espacés, ce graphique est très pratique. Les distances entre les points-lignes (respectivement points-colonnes) correspondent aux distances du Khi² entre les lignes (respectivement entre les colonnes). Les groupes d'âge 25-34, 35-44 et 45-54 sont presque superposés, indiquant des profils très similaires.

La proximité entre les points-lignes et les points-colonnes ne peut pas être interprétée directement sur ce graphique.

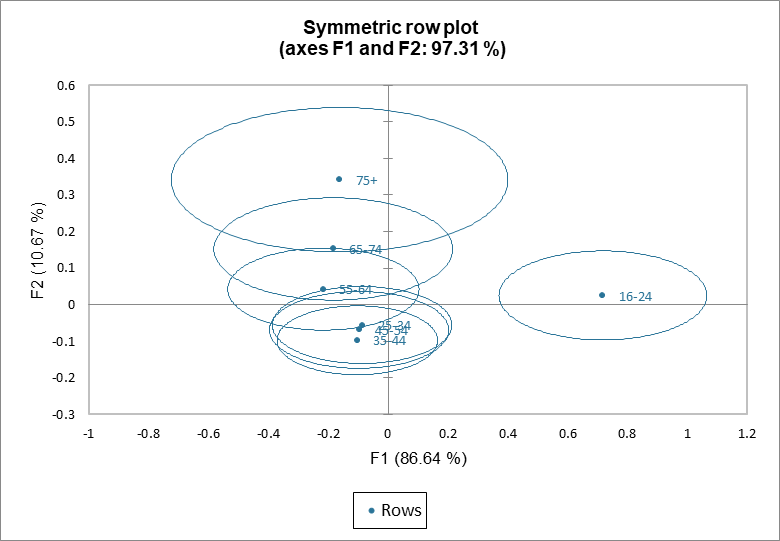
Des ellipses de confiance peuvent être ajoutées sur les graphiques symétriques des lignes ou des colonnes, comme illustré sur le graphique symétrique des lignes ci-dessous. Si l'origine se trouve dans l’ellipse d'une catégorie donnée, cette catégorie ne contribue pas à la dépendance entre les variables. Dans notre exemple, les ellipses confirment que les groupes d'âge 25-34, 34-45 et 45-54 ne contribuent pas à la dépendance entre les variables. Le groupe des 16-24 ans contribuent à la dépendance entre les variables.

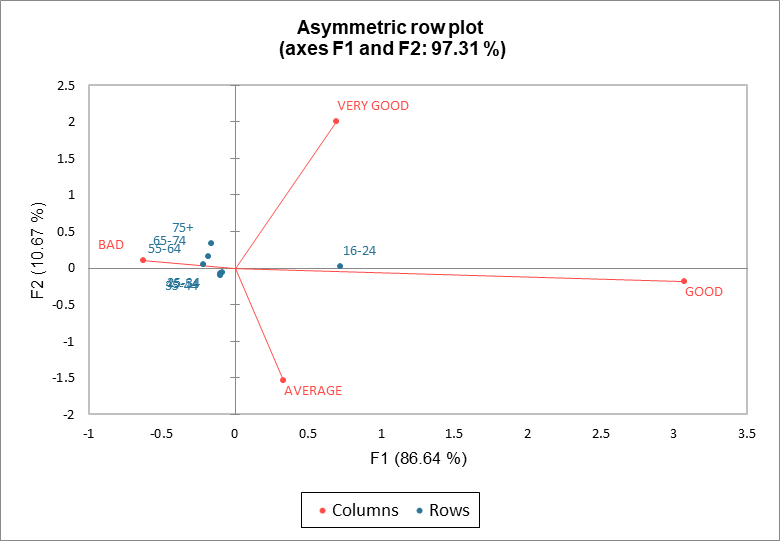
Sur le graphique asymétrique des lignes, les colonnes sont représentées dans l'espace des lignes (coordonnées standard pour les colonnes et coordonnées principales pour les lignes). Inversement, le graphique asymétrique des colonnes correspond aux lignes représentées dans l'espace des colonnes. Les distances entre lignes et colonnes peuvent être interprétées en projetant les points-lignes sur les vecteurs-colonnes. Le choix de la représentation dans l’espace des lignes ou l’espace des colonnes dépend de l’interprétation appropriée. Dans notre exemple, nous choisissons d'interpréter les groupes d'âge dans l'espace des niveaux d'appréciation. La première dimension oppose « BON » à « MAUVAIS ». Le groupe des 16-24 ans comprend une proportion plus grande de « BON » par rapport aux proportions de « BON » dans les autres tranches d'âge. Cependant, cela ne signifie pas que la qualification « BON » a la plus grande proportion parmi les autres proportions au sein du groupe des 16-24 ans. Les profils lignes ne sont pas très différents du profil moyen (points proches de l'origine).

Les coordonnées de contribution des lignes et des colonnes sont ensuite affichées. Les coordonnées de contribution sont obtenues en divisant les coordonnées standard par la racine carrée de la masse de la catégorie donnée.

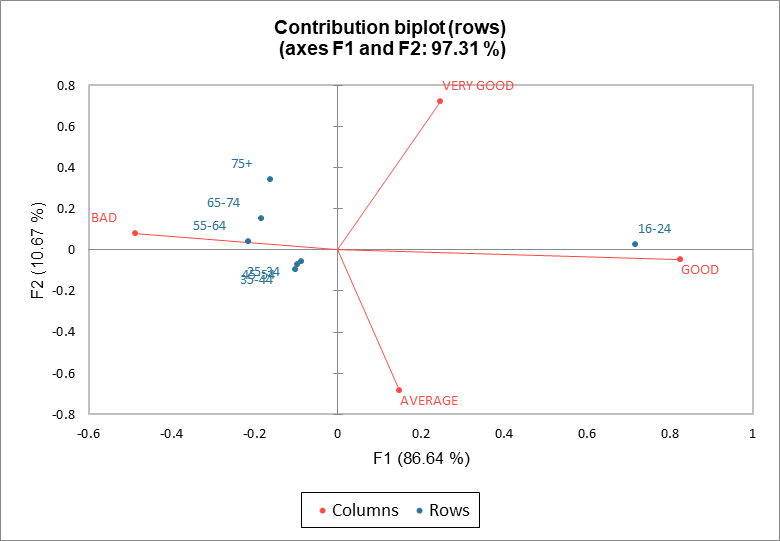
Sur le biplot de contribution des lignes, les lignes sont en coordonnées de contribution et les colonnes sont en coordonnées principales, et inversement pour le biplot de contribution des colonnes. Sur le biplot des contributions des lignes (respectivement des colonnes), les distances des points lignes (respectivement colonnes) à l'origine sont liées à leur contribution au graphique. Dans notre exemple, sur le biplot de contribution des lignes, les positions des points des lignes sont inchangées par rapport au graphique asymétrique. Les points colonnes sont plus proches de l'origine (voir les échelles des deux représentations).

L'Analyse Factorielle des Correspondances est une technique très efficace pour analyser les tableaux de contingence. Lorsque plus de deux variables sont utilisés dans une enquête, la meilleure technique à utiliser est l'Analyse des Correspondances Multiples (MCA).

La vidéo suivante aborde la théorie de l'analyse des correspondances (AC) et sa mise en œuvre dans XLSTAT.