Hauptkomponentenanalyse (HKA) in Excel - Anleitung

Dieses Tutorium wird Ihnen helfen, eine Hauptkomponenten-Analyse (HKA) in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.

Datensatz für die Durchführung einer Hauptkomponenten-Analyse in Excel mit XLSTAT

Die Daten stammen vom US Census Bureau und beschreiben die Bevölkerungsveränderungen von 51 Staaten zwischen 2000 und 2001. Der erste Datensatz wurde in Raten pro 1000 Einwohner transformiert, wobei die Daten für 2001 als Schwerpunkt der Analyse dienen.

Absicht dieses Tutoriums

Unsere Absicht besteht darin, die Korrelation zwischen den Variablen zu analysieren und herauszufinden, ob die Bevölkerungsveränderungen in einigen Staaten sich sehr von denen in anderen Staaten unterscheidet.

Erstellen einer Hauptkomponenten-Analyse mit XLSTAT

• Öffnen Sie XLSTAT

• Wählen Sie den Befehl XLSTAT / Datenanalyse / Hauptkomponentenanalyse aus. Das Dialogfeld Hauptkomponentenanalyse wird angezeigt.

• Wählen Sie die Daten im Excel-Blatt aus. In diesem Beispiel beginnen die Daten in der ersten Zeile, daher ist es schneller und einfacher, die Spaltenauswahl zu verwenden. Das erklärt, warum die Buchstaben, die den Spalten entsprechen, in den Auswahlfeldern angezeigt werden.

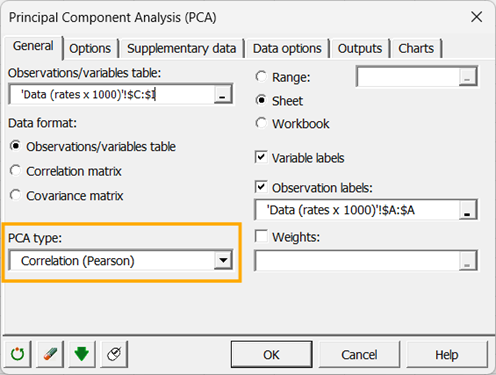
• Wählen Sie im Datenformatfeld Beobachtungen/Variablen aus, aufgrund des Formats der Eingabedaten.

• Wählen Sie im Feld PCA-Typ die Option Korrelation aus. Der PCA-Typ, der während der Berechnungen verwendet wird, ist die Korrelationsmatrix, die dem Pearson-Korrelationskoeffizienten entspricht. Kovarianzmatrizen gewichten Variablen mit höheren Varianzen stärker. Spearman-Korrelationen können geeigneter sein, wenn die PCA auf Variablen mit unterschiedlichen Verteilungen angewendet wird.

• Aktivieren Sie im Reiter Ausgaben die Option, signifikante Korrelationen in Fettdruck anzuzeigen (Signifikanztest).

• Im Reiter Diagramme, um die Beschriftungen auf allen Diagrammen anzuzeigen und um alle Beobachtungen (Beobachtungsdiagramme und Biplots) anzuzeigen, deaktivieren Sie die Filteroption. Wenn es viele Daten gibt, kann das Anzeigen der Beschriftungen die Gesamtdarstellung der Ergebnisse verlangsamen. Das Anzeigen aller Beobachtungen kann die Ergebnisse unleserlich machen. In diesen Fällen wird empfohlen, die zu zeigenden Beobachtungen zu filtern.

• Klicken Sie auf OK, um die Berechnungen zu starten.

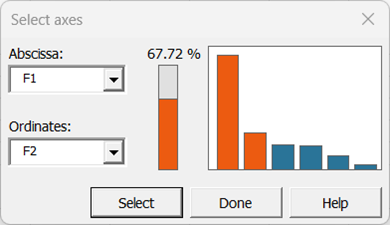
• Bestätigen Sie die Achsen, für die Sie Diagramme anzeigen möchten. In diesem Beispiel werden 67,72 % der Variabilität durch die ersten beiden Faktoren dargestellt, aber es kann nützlich sein, andere Achskombinationen auszuwählen, um die Analyse zu vervollständigen und zu verfeinern, falls relevant.

Interpretieren der Ergebnisse einer Hauptkomponenten-Analyse in Excel mithilfe von XLSTAT

Was ist die Hauptkomponenten-Analyse

Die Hauptkomponenten-Analyse ist eine sehr nützliche Methode zur Analyse numerischer Daten, die in einer Tabelle M Beobachtungen / N Variablen angeordnet sind. Sie haben die Möglichkeit:

• Korrelationen zwischen den N Variablen schnell darzustellen und zu analysieren,

• Die M Beobachtungen (ursprünglich durch die N Variablen beschrieben) auf einer niedrigdimensionalen Karte darzustellen und zu analysieren, die optimale Ansicht für ein Variabilitätskriterium,

• Einen Satz von P unkorrelierten Faktoren zu erstellen

Die Grenzen einer Hauptkomponenten-Analyse ergeben sich aus der Tatsache, dass es sich um eine Projektionsmethode handelt, und manchmal kann die Darstellung zu Fehlinterpretationen führen. Es gibt jedoch einige Tricks, um diese Fallen zu vermeiden.Es ist auch wichtig, zu beachten, dass die HKA ein exploratives statistisches Tool ist und im Allgemeinen nicht zum Testen von Hypothesen geeignet ist. Der Vorteil dieses Aspekts besteht darin, dass HKAs mehrfach durchgeführt werden können, wobei Beobachtungen oder Variablen in jedem Durchlauf hinzugefügt oder entfernt werden können, solange diese Änderung in den Interpretationen begründet werden.

Interpretation einer HKA-Korrelationsmatrix

Das erste zu analysierende Ergebnis ist die Korrelationsmatrix. Wir können sofort sehen, dass die Anteile der Personen unter und über 65 negativ korreliert sind (r = -1). Wir hätten beide Variablen ohne Auswirkung auf die Qualität der Ergebnisse entfernen können. Man erkennt ebenfalls, dass die Zuwanderung aus anderen Staaten der USA sehr wenig mit den anderen Variablen korreliert ist, einschließlich der Auslandseinwanderung. Dies deutet darauf hin, dass die Motivation für einen Umzug bei US-Bürgern und Ausländern verschieden ist.

Interpretation der Eigenwerte in der Hauptkomponenten-Analyse

Die folgende Tabelle mit ihrem zugehörigen Diagramm sind an ein mathematisches Objekt angelehnt, den Eigenwerten, welche die einem einfachen Konzept folgen: Die Qualität der Projektion von N Dimensionen (N ist die Anzahl der Variable, hier 7) auf eine kleinere Anzahl von Dimensionen. In unserem Fall sieht man, dass der erste Eigenwert 3,567 ist und 51 % der Gesamtvariabilität repräsentiert. Dies bedeutet, falls man die Daten auf einer einzigen Achse darstellt, so wird immer noch % der Gesamtvariabilität erhalten bleiben.
Jeder Eigenwert entspricht einem Faktor und jeder Faktor einer Dimension. Ein Faktor ist eine lineare Kombination der Ausgangsvariablen, und alle Faktoren sind unkorreliert (r=0). Die Eigenwerte und die Faktoren werden in absteigender Ordnung gemäß der Variabilität dargestellt (umgewandelt in %).
Allgemein gesprochen gilt Faktor = HKA-Dimension = HKA-Achse

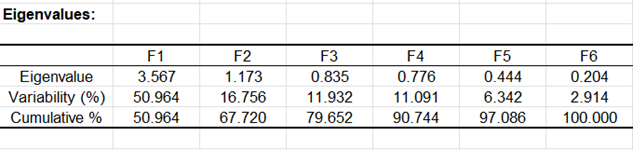
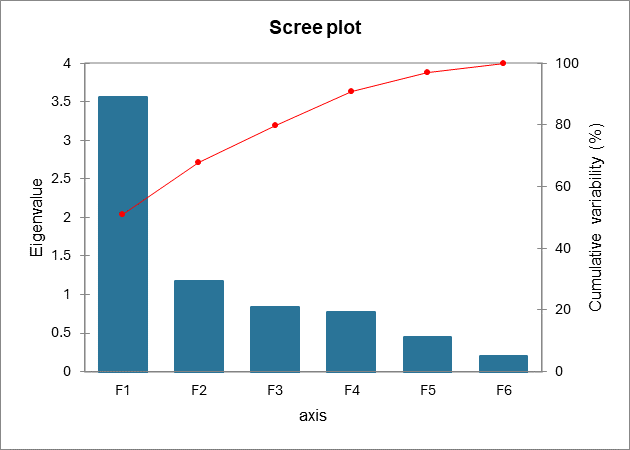
Idealerweise entsprechen die ersten beiden oder drei Eigenwerte einem hohen Prozentsatz der Varianz, so dass die auf den ersten beiden oder drei Faktoren basierenden Diagramme eine gute Abbildungsqualität der ursprünglichen multidimensionalen Tabelle bieten. In diesem Beispiel können wir mithilfe der ersten beiden Faktoren 67,72 % der Ausgangsvariabilität der Daten wiedergeben. Dies ist ein gutes Ergebnis, aber wir müssen vorsichtig sein, wenn wir die Darstellungen interpretieren, da einige Informationen möglicherweise in den nächsten Faktoren versteckt sind. Wir können hier sehen, dass obwohl wir ursprünglich 7 Variablen hatten, die Anzahl der Faktoren nun 6 ist. Dies ist auf die beiden Altersvariablen zurückzuführen, die negativ korreliert sind (-1). Die Anzahl der „nützlichen“ Dimensionen wurde automatisch festgestellt.

Interpretation von Ergebnissen in Bezug auf Variablen in HKA

Die erste Darstellung ist der Korrelationskreis (siehe unterhalb auf den Achsen F1 und F2). Er entspricht einer der Ausgangsvariablen im Faktorbereich. Wenn zwei Variablen weit vom Zentrum entfernt sind, so sind sie: - nah beieinander abgebildet, und daher sind sie signifikant positiv korreliert (r ist nahe an 1), - orthogonal liegend abgebildet, und daher signifikant nicht-korreliert (r nah bei 0), - symmetrisch gegenüberliegend in Bezug auf das Zentrum, und daher signifikant negativ korreliert (r nahe an -1).
Wenn die Variablen nahe am Zentrum des Diagramms liegen, sind einige Informationen auf anderen Achsen aufgetragen und jede Interpretation riskant. Wir könnten beispielsweise versucht sein, zu interpretieren, dass die Variablen Inlandseinwanderung und Auslandseinwanderung korreliert sind, wobei dies jedoch nicht der Fall ist. Dies lässt sich anhand der Korrelationsmatrix oder im Korrelationskreis der Achsen F1 und F3 sehen.

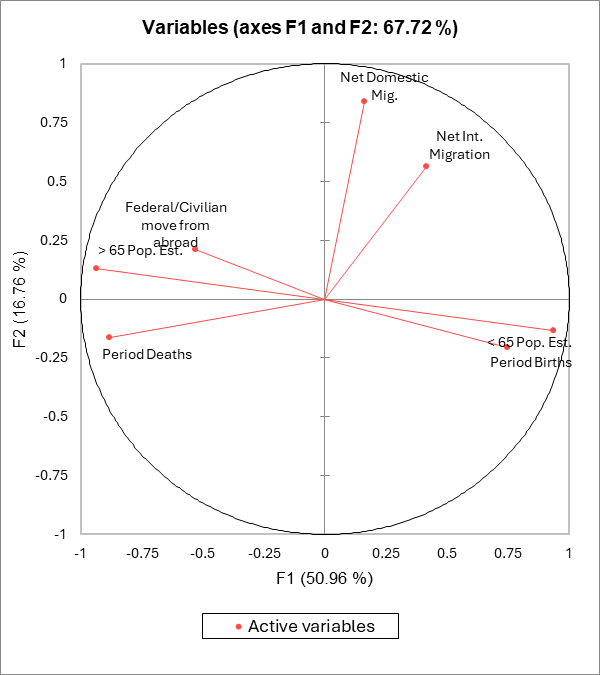
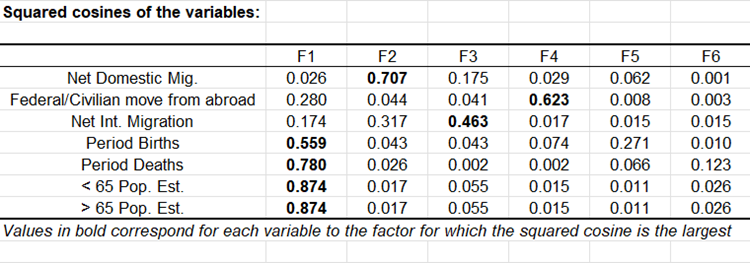
Die Korrelationskreise sind ebenfalls nützlich zur Interpretation der Signifikanz der Achsen. In unserem Fall ist die horizontale Achse klar an das Alter und die Bevölkerungserneuerung angelehnt, wogegen die vertikale Achse essentiell auf die Inlandseinwanderung aufbaut. Diese Trends sind hilfreich bei der Interpretation der nächsten Darstellung. Um zu überprüfen, ob eine Variable stark an eine Achse gebunden ist, reicht es aus die Tabelle der quadrierten Cosinuswerte zu betrachten: Je größer der quadrierte Cosinuswert ist, desto mehr ist die Variable an die entsprechende Achse gebunden. Je näher der quadrierte Cosinuswert einer gegebenen Variable bei Null liegt, desto vorsichtiger müssen Sie bei der Interpretation der Ergebnisse hinsichtlich der Trends auf den entsprechenden Achsen sein. Beim Betrachten dieser Tabelle können wir sehen, dass die Trends für die Auslandseinwanderung am besten auf der F2/F3-Darstellung zu sehen sind.

Interpretieren von Ergebnissen in Bezug auf Beobachtungen in HKA

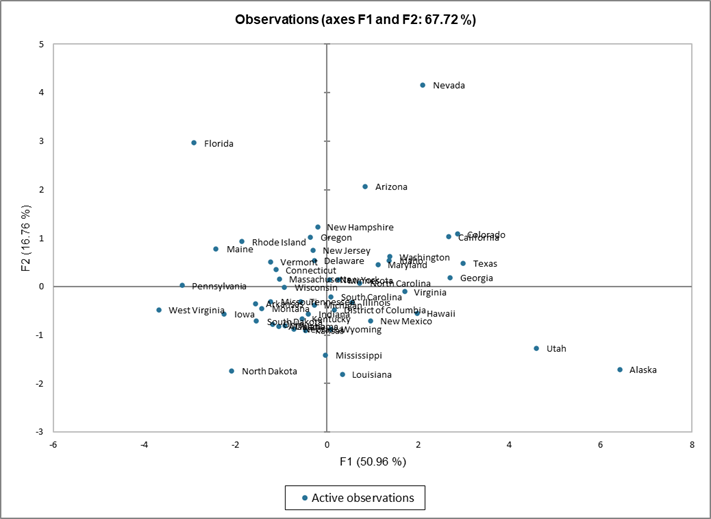
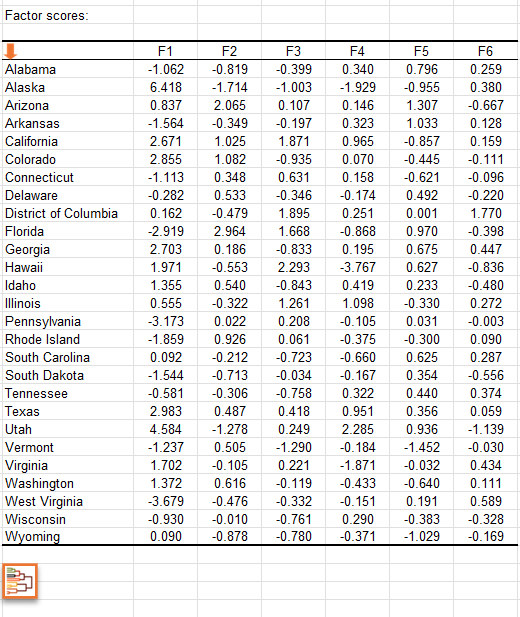
Das nächste Diagramm kann der Hauptabsicht der Hauptkomponenten-Analyse (HKA) entsprechen. Es erlaubt die Darstellung der Beobachtungen auf einer zweidimensionalen Karte, um so die Trends zu identifizieren. Man sieht in unserem Beispiel, dass die Demografie von Nevada und Florida einzigartig ist, genau wie die Demografie von Utah und Alaska, zwei Staaten, die gemeinsame Merkmale haben. Wen wir zur Tabelle zurückgehen, können wir bestätigen, dass Utah und Alaska eine geringe Bevölkerungsrate von Menschen über 65 Jahren haben. Utah hat die höchste Geburtenrate in den USA, und auch Alaska steht auf der Liste weit oben.

Es besteht ebenso die Möglichkeit, Biplots anzuzeigen, in denen gleichzeitig Variablen und Beobachtungen im HKA-Bereich dargestellt werden können.

Note on the usage of Principal Component Analysis

Principal component analysis is often performed before a regression, to avoid using correlated variables, or before clustering the data, to have a better overview of the variables. The number of clusters might sometimes be a simple guess based on the maps. The above demographic data have also been used in the tutorial on hierarchical clustering. The ">65 pop" variable has been removed as its inclusion would double the weight of the age variables in the analysis.

Going further: adding supplementary variables to the PCA

It is possible to add supplementary variables to the PCA after it has been computed. This may help increasing interpretation quality. In XLSTAT, those variables can be selected under the Suppl. Data tab of the PCA dialog box. Supplementary variables can be divided into two types:
- Qualitative supplementary variables: they allow to color observations on the map according to the category they belong to. In this tutorial's example, we could have added a column defining if a state is mostly republican or mostly democrat. 
- Quantitative supplementary variables: these variables can be added to see how they correlate with the group of variables that have been used to build the PCA. In the case where PCA is performed before a regression, the explanatory variables can be used to construct the PCA while the dependent variable can be added as a supplementary variable. This may help to roughly detect which explanatory variables could have the strongest effects on the dependent variable.

Klicken Sie hier, um zu sehen, wie Sie die Ergebnisse der AHC-Analyse interpretieren können.

Sehen Sie sich unser Video zur PCA-Analyse an Das folgende Video hilft Ihnen, die PCA und ihre Implementierung in XLSTAT besser zu verstehen.