Análisis de Componentes Principales en Excel

Este tutorial muestra cómo configurar e interpretar un Análisis de componentes principales (ACP) en Excel usando el software estadístico XLSTAT.

Datos para ejecutar un Análisis de Componentes Principales con XLSTAT

Los datos provienen de la Oficina del Censo de USA (US Census Bureau) y describen los cambios en la población de 51 estados entre 2000 y 2001. El conjunto de datos iniciales ha sido transformado en tasas por 1000 habitantes, con los datos de 2001 sirviendo como foco para el análisis.

Objetivo de este tutorial

Nuestro objetivo es analizar las correlaciones entre las variables y encontrar si los cambios en la población de algunos estados son muy diferentes de los observados en otros estados.

Configuración de un Análisis de Componentes Principales en Excel usando XLSTAT

• Abra XLSTAT

• Seleccione el comando XLSTAT / Análisis de datos / Análisis de componentes principales. Aparecerá el cuadro de diálogo de Análisis de Componentes Principales.

• Seleccione los datos en la hoja de Excel. En este ejemplo, los datos comienzan desde la primera fila, por lo que es más rápido y fácil usar la selección por columnas. Esto explica por qué las letras correspondientes a las columnas se muestran en los cuadros de selección.

• Seleccione Observaciones/variables en el campo Formato de datos debido al formato de los datos de entrada.

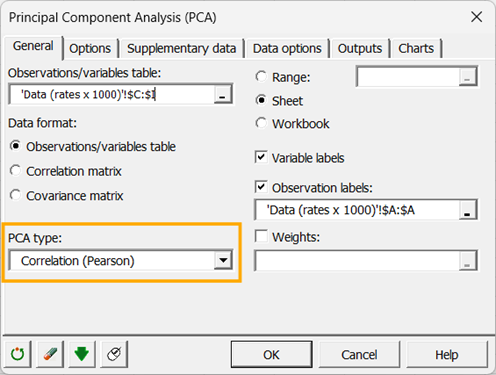
• Seleccione Correlación en el campo Tipo de ACP. El tipo de ACP que se utilizará durante los cálculos es la matriz de correlación, que corresponde al coeficiente de correlación de Pearson. Las matrices de covarianza asignan más peso a las variables con mayores varianzas. Las correlaciones de Spearman pueden ser más apropiadas al ejecutar la ACP en variables con diferentes distribuciones.

• En la pestaña Salidas, active la opción para mostrar las correlaciones significativas en negrita (Prueba de significancia).

• En la pestaña Gráficos, para mostrar las etiquetas en todos los gráficos y para mostrar todas las observaciones (gráficos de observaciones y biplots), desmarque la opción de filtrado. Si hay muchos datos, mostrar las etiquetas puede ralentizar la visualización global de los resultados. Mostrar todas las observaciones podría hacer que los resultados sean ilegibles. En estos casos, se recomienda filtrar las observaciones a mostrar.

• Haga clic en OK para iniciar los cálculos.

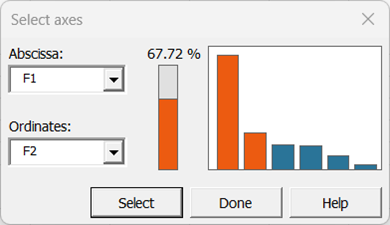
• Confirme los ejes para los que desea mostrar gráficos. En este ejemplo, el 67,72 % de la variabilidad está representada por los dos primeros factores, pero puede ser útil seleccionar otras combinaciones de ejes para completar y refinar el análisis si es relevante.

Interpretación de un Análisis de Componentes Principales en Excel usando XLSTAT

Qué es un Análisis de Componentes Principales

El análisis de componentes principales es un método muy útil para analizar datos numéricos estructurados en una tabla de M observaciones / N variables. Permite:

• Visualizar y analizar rápidamente las correlaciones entre las N variables,

• Visualizar y analizar las M observaciones (inicialmente descritas por las N variables) en un mapa de menos dimensiones, la vista óptima para un criterio de variabilidad,

• Construir un conjunto de P factores correlacionados

Los límites del análisis de componentes principales se derivan del hecho de que es un método de proyección, y en ocasiones la visualización puede conducir a interpretaciones falsas. Disponemos sin embargo de algunos trucos para evitar estos inconvenientes.Es asimismo importante advertir que el ACP es una herramienta estadística exploratoria y no permite en general someter hipótesis a prueba. La ventaja de este aspecto es que el ACP puede ejecutarse repetidas veces añadiendo o eliminando observaciones de las variables en cada ejecución, en la medida en que esas manipulaciones estén justificadas en las interpretaciones.

Cómo interpretar una matriz de correlaciones ACP

El primer resultado a consultar es la matriz de correlaciones. Podemos ver de inmediato que las tasas de personas por encima y por debajo de 65 tienen una correlación negativa (r = -1). Cualquiera de las dos variables podría haberse eliminado sin que ello tuviera efecto sobre la calidad de los resultados. También podemos ver que la migración neta doméstica tiene una baja correlación con las otras variables, incluyendo la migración internacional neta. Esto significa que los ciudadanos de Estados Unidos y los no nacionales pueden estar trasladándose a un estado por razones de distinto tipo.

Cómo interpretar los valores propios (eigenvalues) en un Análisis de Componentes Principales

La siguiente tabla y su gráfico correspondiente se relacionan con un objeto matemático, los valores propios, que reflejan la calidad de la proyección desde la tabla inicial de N dimensiones (N = 7 en este ejemplo) a un menor número de dimensiones. En este ejemplo, podemos ver que el primer valor propio es igual a 3.567 y representa el 51% de la variabilidad total. Esto significa que si representamos los datos sobre un solo eje, aun así seremos capaces de ver un % de la variabilidad total de los datos.
Cada valor propio corresponde a un factor, y cada factor a una una dimensión. Un factor es una combinación lineal de las variables iniciales, y todos los factores son no-correlacionados (r = 0). Los valores propios y los factores correspondientes están ordenados (en orden descendente) en función de la cantidad de la variabilidad inicial que representan (convertidos a%).
En términos generales, factor = dimensión ACP = eje ACP

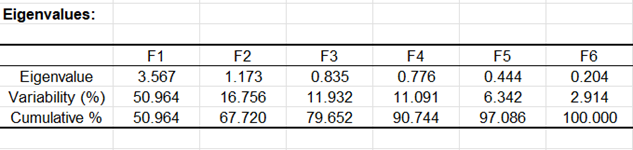
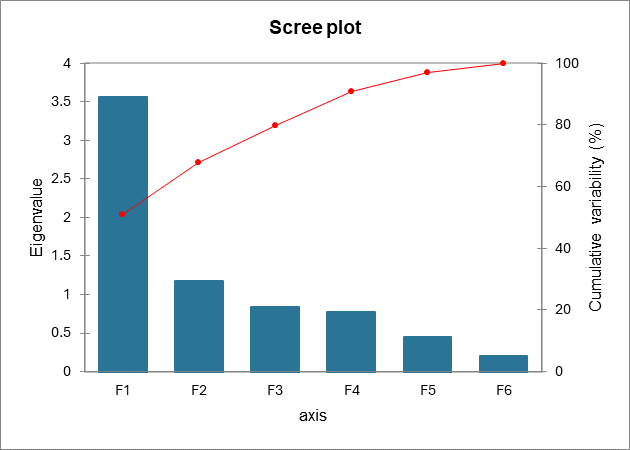
Idealmente, los dos o tres primeros valores propios corresponderán a un alto % de la varianza, lo cual nos asegura que los mapas a partir de los dos o tres primeros factores son una proyección de buena calidad de la tabla multidimensional inicial. En este ejemplo, los dos primeros factores permiten representar el 67,72% de la variabilidad inicial de los datos. Este es un buen resultado, pero tendremos que tener cuidado al interpretar los mapas, ya que alguna información podría estar oculta en los siguientes factores. Podemos ver aquí que, a pesar de que inicialmente teníamos 7 variables, el número de factores es 6. Esto se debe a las dos variables de edad, que tienen una correlación negativa (-1). El número de dimensiones "útiles" se ha detectado automáticamente.

Cómo interpretar los resultados relativos a las variables en ACP

El primer mapa se denomina círculo de correlaciones (ver más abajo, el mapa de los ejes F1 y F2). Muestra una proyección de las variables iniciales en el espacio factorial. Cuando dos variables están lejos del centro, tenemos varias posibilidades: si están próximas una a la otra, están positivamente correlacionadas (i.e., r está próximo a 1); si son ortogonales, no están correlacionadas (i.e., r está próximo a 0); si están en lados opuestos con respecto al centro están negativamente correlacionadas (i.e., r está próximo a -1).
Cuando las variables están próximas al centro, alguna información es transportada a otros ejes, y cualquier interpretación podría resultar peligrosa. Por ejemplo, podríamos estar tentados a interpretar que existe correlación entre Migración doméstica neta y Migración internacional neta aunque, de hecho, no existe. Esto se puede confirmar ya sea observando la matriz de correlaciones, o examinando el círculo de correlación en los ejes F1 y F3.

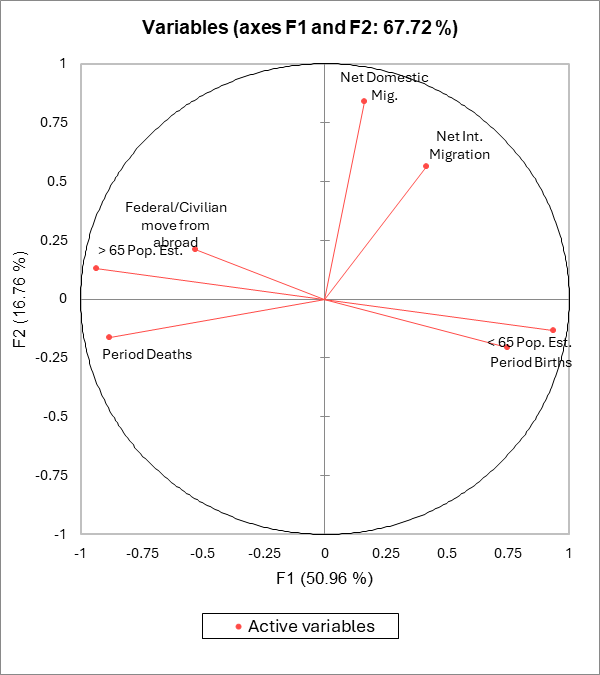
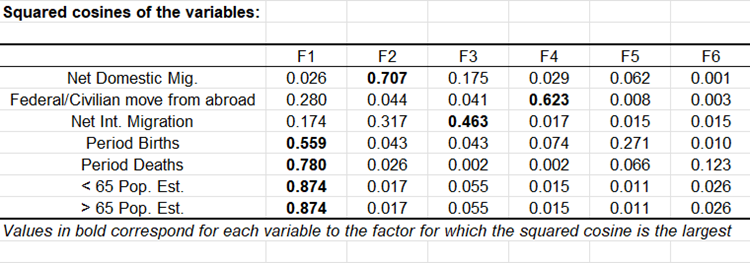
El círculo de correlaciones es útil para interpretar el significado de los ejes. En este ejemplo, el eje horizontal está relacionado con la edad y la renovación de la población, y el eje vertical con la migración interna. Estas tendencias serán útiles para interpretar el siguiente mapa. Para confirmar que una variable está bien vinculada con un eje, podemos echar un vistazo a la tabla de cosenos al cuadrado: cuanto mayor es el coseno al cuadrado, mayor es el vínculo con el eje correspondiente. Cuanto más se acerca el coseno al cuadrado de una variable dada a cero, más cuidado debemos tener a la hora de interpretar los resultados en términos de tendencias sobre el eje correspondiente. Al examinar esta tabla, podemos ver que las tendencias de la migración internacional podrían verse mejor en un mapa F2 / F3.

Cómo interpretar los resultados relativos a las observaciones en ACP

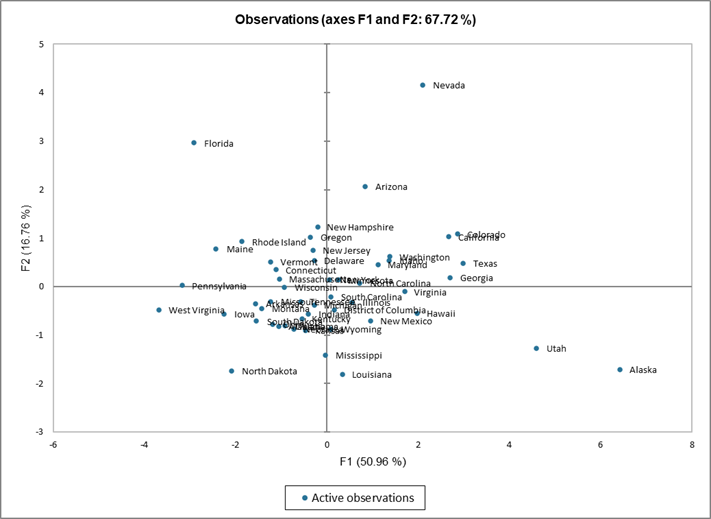
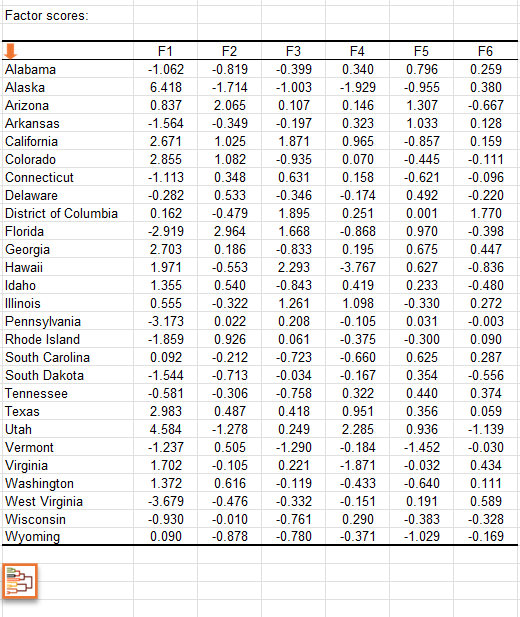
El siguiente gráfico podría ser el objetivo final del Análisis de Componentes Principales (ACP). Nos permite examinar las observaciones en un mapa bidimensional, así como identificar tendencias. Podemos ver que la demografía de Nevada y Florida son únicas, como lo son las demografías de Utah y Alaska, dos estados que comparten características comunes. Volviendo a la tabla, podemos confirmar que Utah y Alaska tienen una tasa de población baja de personas mayores de 65 años. Utah tiene la tasa de natalidad más alta de los Estados Unidos, y Alaska ocupa también un lugar destacado.

Es asimismo posible mostrar biplots, que son representaciones simultáneas de variables y observaciones en el espacio ACP.

Nota sobre el uso del Análisis de Componentes Principales

El análisis de componentes principales con frecuencia se lleva a cabo antes de una regresión, con el fin de evitar usar variables correlacionadas, o antes de hacer un análisis cluster de los datos, para tener una mejor visión general de las variables. El número de clusters podría en ocasiones ser un una simple estimación basada en los mapas. Los datos demográficos anteriores se han usado asimismo en el tutorial sobre clusterización jerárquica. Se ha eliminado la variable ">65 pop", ya que su inclusión doblaría el peso de la variable Edad en el análisis.

Un paso más: adición de variables suplementarias al ACP

Es posible añadir variables suplementarias al ACP tras haber realizado los cálculos, lo que puede ayudar a aumentar la calidad de la interpretación. En XLSTAT, se pueden seleccionar estas variables en la pestaña Datos suplementarios del cuadro de diálogo del ACP. Las variables suplementarias pueden dividirse en dos tipos:

• Variables suplementarias cualitativas: permiten colorear las observaciones del mapa según la categoría a la que pertenecen. En el ejemplo de este tutorial, podríamos haber añadido una columna que define si un estado es de mayoría republicana o de mayoría demócrata.

• Variables suplementarias cuantitativas: estas variables se pueden añadir para ver cómo se correlacionan con el grupo de variables utilizadas para construir el ACP. En el caso en que el ACP se lleva a cabo antes de una regresión, se pueden utilizar las variables explicativas para construir el ACP, en tanto que la variable dependiente se puede añadir como variable suplementaria. Esto puede ayudar a detectar más o menos cuáles de las variables explicativas podrían tener los efectos más fuertes sobre la variable dependiente.

Haga clic aquí para ver cómo interpretar los resultados del análisis AHC.