Test de Friedman, tutoriel dans Excel
Exécution et interprétation du test non-paramétrique de Friedman sur k échantillons appariés dans Excel avec XLSTAT.
Jeu de données pour réaliser un test de Friedman dans Excel avec XLSTAT
Les données correspondent à une étude sensorielle au cours de laquelle on a demandé à 10 experts de noter au cours de deux tests en aveugle la dureté de fromages sur une échelle de 0 à 5. Notre but est de déterminer si la différence de dureté entre les fromages est significative ou non.
Paramétrer un test de Friedman dans XLSTAT
Cliquez sur le menu XLSTAT / Tests non paramétriques / Comparaison de k échantillons, ou cliquez sur le bouton correspondant de la barre Tests non paramétriques (voir ci-dessous).
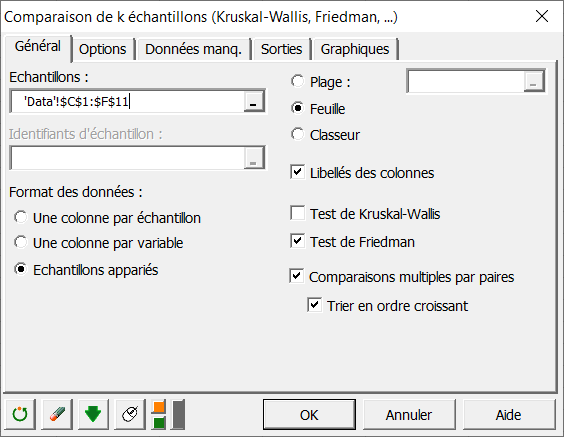
Une fois le bouton cliqué, la boîte de dialogue apparaît.
Activez l'option Echantillons appariés, puis sélectionnez les données sur la feuille Excel : sélectionnez avec la souris les quatre colonnes de données correspondant aux quatre fromages.
Comme le nom des fromages est contenu dans la première ligne de données, laissez activée l'option Libellés des colonnes.
Activez ensuite l'option Comparaisons multiples afin que l'on puisse déterminer quels fromages sont différents si le test de Friedman nous amenait à rejeter l'hypothèse nulle de similitude entre les fromages.
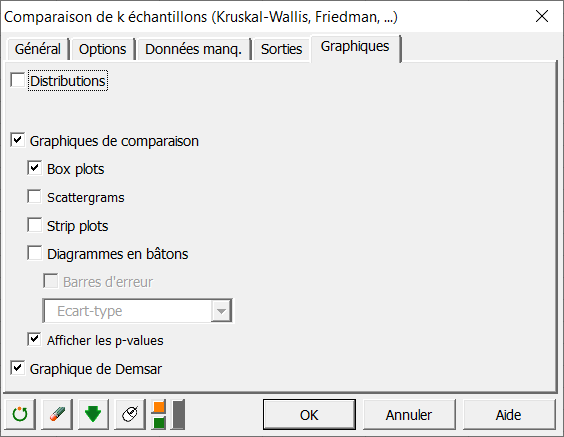
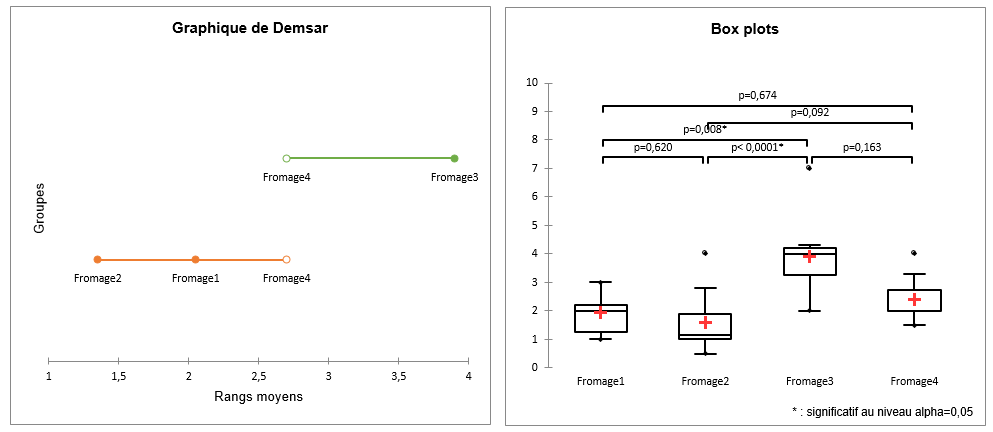
Dans l'onglet Graphiques, plusieurs options sont disponibles pour visualiser les résultats de tests de comparaisons multiples comme le graphique de Demšar.
Les calculs commencent lorsque vous cliquez sur le bouton OK puis les résultats sont affichés.
Interpréter un test non paramétrique de Friedman pour la comparaison de k échantillons
Dans le premier tableau sont affichées la statistique Q de Friedman et la p-value correspondante. La p-value nous indique que la probabilité de rejeter l'hypothèse nulle alors qu'elle serait vraie est inférieure à 0.0001. Dans ce cas, on peut en toute confiance rejeter l'hypothèse nulle d'absence de différence significative entre les fromages.

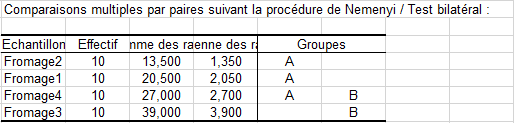
Les résultats suivants nous permettent de repérer quels fromages sont différents des autres, comme on le ferait avec des comparaisons multiples en ANOVA. Afin de prendre en compte que les comparaisons sont effectuées sur k groupes, la procédure de Nemenyi est utilisée. Elle est appliquée au niveau de signification alpha. Du tableau de synthèse ci-dessous, on déduis que les fromages 2 et 3, et 1 et 3 sont différents. En revenant aux données, le fromage 3 est clairement celui qui est perçu comme étant le plus dur.
N'hésitez pas à consulter notre guide de choix de test statistique.
Cet article vous a t-il été utile ?
- Oui
- Non