Diagrammes de probabilité, tutoriel dans Excel
Ce tutoriel explique comment mettre en place et interpréter un diagramme de probabilité dans Excel avec le logiciel XLSTAT.
Les diagrammes de probabilité
Les diagrammes de probabilité sont une méthode ancienne (Hazen, 1914), qui a été peu à peu perfectionnée et largement utilisée, notamment au travers de l'utilisation de papier de probabilité. Ils sont particulièrement utiles pour contrôler visuellement si un échantillon suit une distribution donnée.
Jeu de données pour mettre en place un diagramme de probabilité
Les données contiennent des notes, variant de 0 à 20, obtenues par un groupe d'élèves de terminal (N = 1000) lors d’un examen de mathématiques. Le but est d’identifier le pourcentage d’élèves avec une très bonne performance, soit les élèves qui ont une note supérieure à 17. Nous allons créer un diagramme de probabilité afin de détecter la distribution qui s’ajuste le mieux et ensuite identifier le pourcentage en question.
Paramétrer un diagramme de probabilité dans XLSTAT
Sélectionnez le menu XLSTAT / Visualisation des données / Diagramme de probabilité.
 Une fois que vous avez cliqué sur le bouton, la boîte de dialogue des Diagrammes de probabilité s'affiche comme ci-dessous :
Une fois que vous avez cliqué sur le bouton, la boîte de dialogue des Diagrammes de probabilité s'affiche comme ci-dessous :
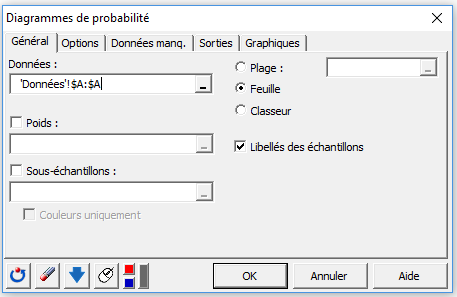 Dans l’onglet Général, sélectionnez la colonne A dans le champ Données. Ensuite, activez l’option Libellés des échantillons puisque la première ligne des données contient un libellé.
Dans l’onglet Général, sélectionnez la colonne A dans le champ Données. Ensuite, activez l’option Libellés des échantillons puisque la première ligne des données contient un libellé.
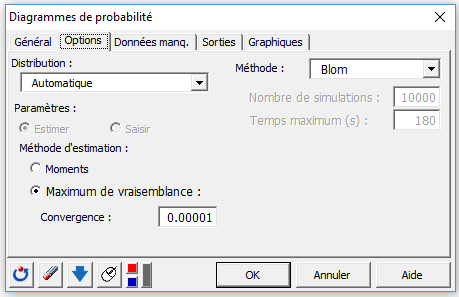 Dans l’onglet Options, choisissez Automatique dans le champ Distribution afin qu'XLSTAT identifie la distribution la plus adéquate sur la base d’un test de Kolmogorov.
Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués et les résultats sont affichés sur une nouvelle feuille.
Dans l’onglet Options, choisissez Automatique dans le champ Distribution afin qu'XLSTAT identifie la distribution la plus adéquate sur la base d’un test de Kolmogorov.
Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués et les résultats sont affichés sur une nouvelle feuille.
Interprétation du diagramme de probabilité
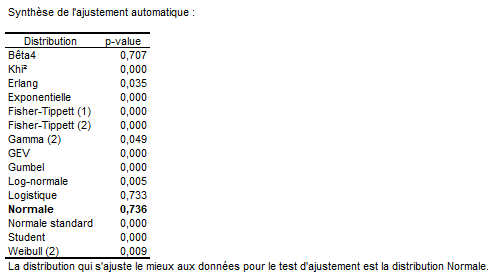
Le premier résultat affiché est la synthèse de l’ajustement automatique suivie des paramètres estimés. La distribution qui s’ajuste le mieux aux données pour le test Kolmogorov est la distribution Normale avec une p-value égale à 0,736. Etant donné que la p-value est supérieure au niveau de signification seuil alpha=0,05, on ne peut pas rejeter l'hypothèse nulle que l’échantillon suit une loi Normale.
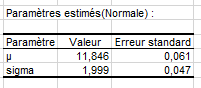
 Les paramètres estimés de la distribution normale (mu, sigma) sont affichés dans le tableau ci-dessous :
Les paramètres estimés de la distribution normale (mu, sigma) sont affichés dans le tableau ci-dessous :
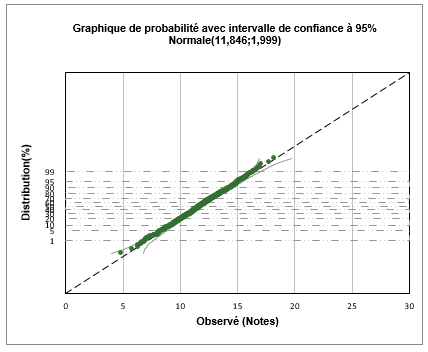
 Le diagramme de probabilité est ensuite affiché. La note égale à 17 représente environ le 99e percentile. Nous pouvons alors conclure qu’environ 99% d’élèves ont obtenu des notes variant de 0 à 17 et 1% d’élèves ont obtenu des notes supérieures à 17.
Le diagramme de probabilité est ensuite affiché. La note égale à 17 représente environ le 99e percentile. Nous pouvons alors conclure qu’environ 99% d’élèves ont obtenu des notes variant de 0 à 17 et 1% d’élèves ont obtenu des notes supérieures à 17.
Cet article vous a t-il été utile ?
- Oui
- Non