Run repeated measures ANOVA using mixed models
This tutorial will help you set up and interpret a Repeated Measures ANOVA using Restricted Maximum Likelihood (REML) in Excel with the XLSTAT software.
Dataset for repeated measures ANOVA using the mixed models
The data correspond to an experiment in which a treatment for depression is studied. Two groups of patients (1: control / 2: treatment) have been followed at five different times (0: pre-test, 1: one month post-test, 3: 3 months follow-up and 6: 6 months follow-up). The dependant variable is a depression score.
We have performed a repeated measures ANOVA in order to determine the effect of the treatment and the effect of time on the depression score. The repeated measures ANOVA model is the same as the classical ANOVA model with interactions:
![]()
We have two fixed factors (time and group) and one interaction factor (time*group). The difference between classical ANOVA and repeated measures ANOVA is that measures on the same patient at different times are not supposed to be independent and, thus, the covariance matrix of e is not diagonal.
XLSTAT uses the mixed models theory to treat repeated measures ANOVA and this raises some differences. Some supplementary options are available like the choice between many covariance structures for the covariance matrix of the error term. Throughout this tutorial we will use the compound symmetry structure. Please consult the XLSTAT help for more details on covariance structures.
Data structure for repeated measures ANOVA
Data should have a particular shape when using the mixed model methodology for repeated measures ANOVA. All the measures have to be on the same column with:
- a factor called repeated factor which indicates what repetition is associated to this measure
- a factor called subject factor which indicates what subject is associated to this measure.
In our example, each patient will appear in 4 different lines. The data has to be in the following form:

If your data is in a different form, one column for each measure, you should transform it in order to obtain the preceding structure.
Setting up the repeated measures ANOVA using the mixed models
After opening XLSTAT, select the XLSTAT / Modeling data / Repeated measures ANOVA command, or click on the corresponding button of the Modeling data toolbar (see below).

Once you've clicked on the button, the repeated measures ANOVA dialog box appears. Select the data on the Excel sheet.
The Dependent variable (or variable to model) is here the "dv".
Our aim is to determine the effect of the group, the time and the interaction between the two on the variability of the depression score.
As we selected the column title for the variables, we left the option Variable labels activated.
"Repeated" and "subject" factors must be selected as explanatory variables.
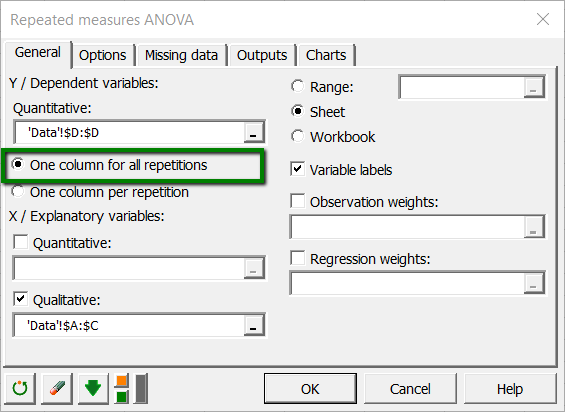
The interactions option is activated on the options tab, and the maximum level of interaction is set to 2.
We left the constraint option at a1=0, meaning that we want the model to be built on the assumption that the control group has the standard effect on the score. Although you have to apply a constraint to the model in ANOVA for theoretical reasons, it will not affect the results (goodness of fit). The only difference it makes is in the actual writing of the model.
The covariance structure selected is the default one which is compound symmetry.

Once you have clicked on the OK button, a dialog box is displayed so that you can choose which factors have to be taken into account in the model. The fixed effects are "time", "group" and "time*group", the repeated factor is "time" and the subject factor is "subj".
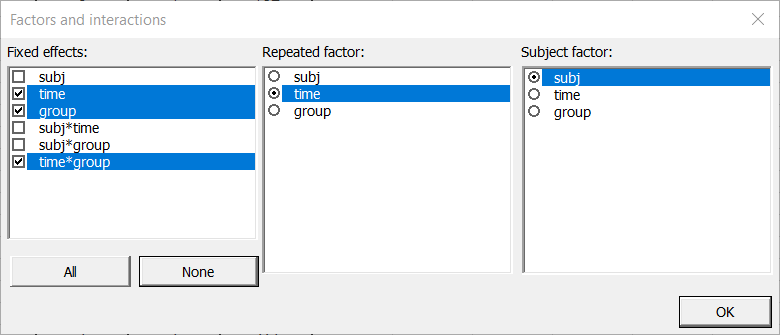 Note: A factor cannot be the subject factor and a fixed effect at he same time. Repeated and subject factors have to be different and both qualitative.
Note: A factor cannot be the subject factor and a fixed effect at he same time. Repeated and subject factors have to be different and both qualitative.
Once you have clicked on the OK button, the computation starts. The results will then be displayed.
Interpreting the results of a repeated measures ANOVA using the mixed models
The first results displayed by XLSTAT are the goodness of fit coefficients.
 Model parameters are obtained using the restricted maximum likelihood (REML) method and will be different as when a classical ANOVA model is applied. All indexes are used to compare models with different covariance structures.
Model parameters are obtained using the restricted maximum likelihood (REML) method and will be different as when a classical ANOVA model is applied. All indexes are used to compare models with different covariance structures.
Covariance parameters are displayed on the next table with their associated Z test. We can see that both parameters are significant.
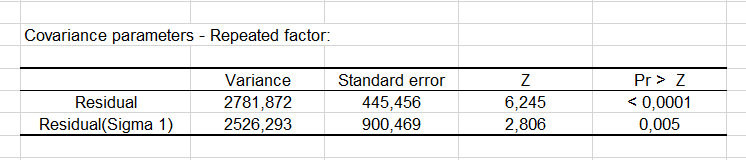
Model implied covariance and correlation matrix can as well be displayed.
The null model likelihood ratio test compares the model obtained with the specified covariance structure and the model obtained with the classical diagonal covariance structure. The obtained p-value can be used to assess the significance of the model fit.
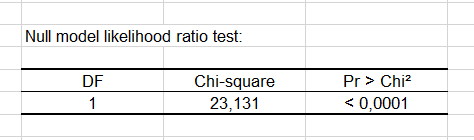
We can see that choosing the compound symmetry structure has a positive effect on the model fit.
The type III tests of fixed effects show that all factors have significant effects on the depression score. These test are very important, they replace the Type III SS of the classical ANOVA model.
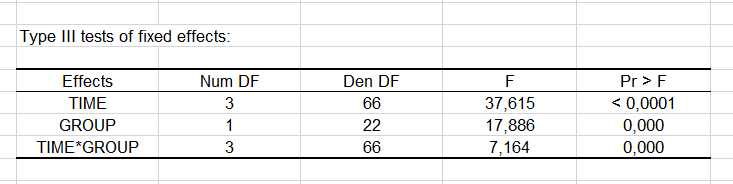
From the results displayed in the Type III table, we can see that the "Time" variable is the one that has the highest impact on the model. When we look at the model parameters (see below), we can see that time 1, 3 and 6 have a negative impact on the depression score. Patients are less depressed as time passes. Being in the treatment group has also a negative impact on the depression score.
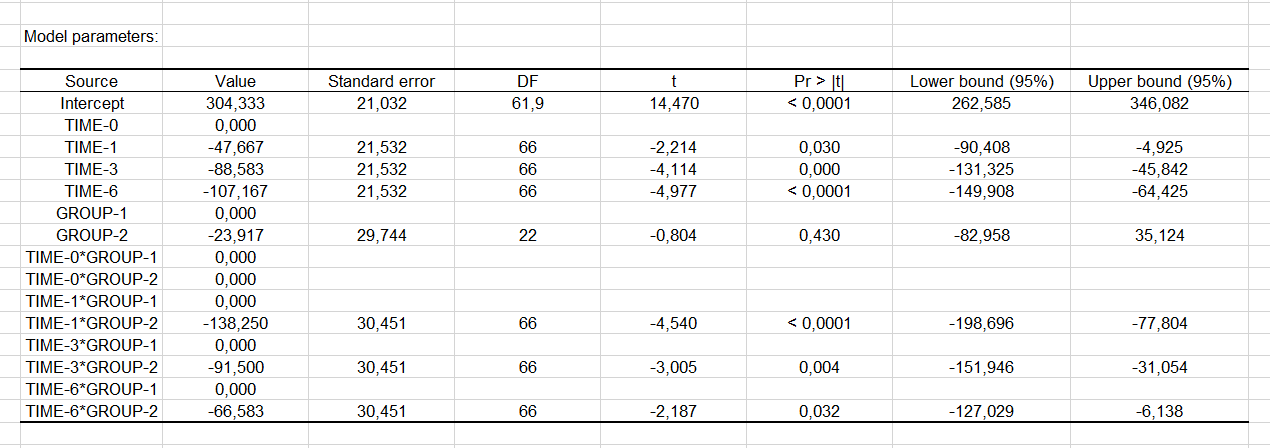
The table depicted above can be used to analyze the impact of the explanatory variables on the depression score and/or to predict the average yield in a situation not yet covered by the experiment, such as the time 6 with the treatment group. In this particular example, the average depression score would be 107.1, given the fact that the influence of the interaction is unknown.
This study has shown that both time and treatment have both a negative significant impact on the depression score.
Some other output can be useful and are available in XLSTAT like residuals, residuals charts, least square means charts…
Was this article useful?
- Yes
- No