Wiederholte Messungen in einer ANOVA mittels Mischmodellen durchführen
Dieses Tutorium wird Ihnen helfen, eine ANOVA mit wiederholten Messungen anhand von eingeschränkter maximaler Wahrscheinlichkeit (REML) in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.
Datensatz für ANOVA mit wiederholten Messungen anhand der gemischten Modelle
Die Daten entsprechen einem Experiment, bei dem ein Medikament zur Behandlung von Depressionen untersucht wurde. Zwei Patientengruppen (1 = Kontrolle, 2 = Behandlung) wurden über 5 verschiedene Phasen verfolgt (0= Vortest, 1= ein Monat nach dem Test, 3 = Nachuntersuchung nach 3 Monaten und 6 = Nachuntersuchung nach 6 Monaten). Die abhängige Variable ist das Depressionspotential.
Es wurde eine ANOVA mit wiederholten Messungen durchgeführt, um den Effekt der Behandlung und den zeitlichen Einfluss auf das Depressionspotential zu bestimmen. Das ANOVA-Modell mit wiederholten Messungen ist gleich dem klassischen ANOVA-Modell mit Interaktionen:
![]()
Es liegen zwei fixe Faktoren (Zeit und Gruppe) und ein Interaktionsfaktor (Zeit*Gruppe) vor. Der Unterschied zwischen der klassischen ANOVA und der ANOVA mit wiederholten Messungen ist, dass Messungen für denselben Patienten zu verschiedenen Zeitpunkten als nicht unabhängig vorausgesetzt werden, und daher die Kovarianzmatrix von e keine Diagonalmatrix ist.
XLSTAT benutzt die Theorie der gemischten Modelle zur Behandlung der ANOVA mit wiederholten Messungen, was zu einigen Unterschieden führt. Einige zusätzliche Optionen sind verfügbar, wie die Wahl zwischen vielen verschiedenen Kovarianzstrukturen für die Kovarianzmatrix des Fehlerterms. Im Laufe dieses Tutorials, wird die zusammengesetzte Symmetrie als Struktur benutzt. Bitte lesen Sie in der XLSTAT-Hilfe nach, um mehr Einzelheiten über die Kovarianzstrukturen zu erfahren.
Datenstruktur für ANOVA mit wiederholten Messungen
Die Daten sollten in einer speziellen Form vorliegen, um die gemischten Modelle für ANOVA mit wiederholten Messungen durchzuführen. Alle Messungen müssen in einer einzigen Spalte vorliegen:
- Mit einem Faktor, der auch wiederholter Faktor genannt wird und der angibt, zu welcher Wiederholung die vorliegende Messung gehört
- Mit einem Faktor, der auch Subjektfaktor genannt wird und der angibt, welchem Subjekt diese Messung zugeordnet wird.
In unserem Beispiel taucht jeder Patient in 4 verschiedenen Zeilen auf. Die Daten liegen in der folgenden Form vor:
 Falls Ihre Daten eine andere Form aufweisen, eine Spalte für jede Messung, so müssen Sie die Daten transformieren, um die oben erwähnte Struktur zu erhalten.
Falls Ihre Daten eine andere Form aufweisen, eine Spalte für jede Messung, so müssen Sie die Daten transformieren, um die oben erwähnte Struktur zu erhalten.
Einrichten der ANOVA mit wiederholten Messungen anhand der gemischten Modelle
Nach dem Start von XLSTAT wählen Sie den XLSTAT/Modellierung der Daten/ANOVA mit wiederholten Messungen Befehl oder klicken Sie auf den zugehörigen Button in der "Modellierung der Daten" Toolbar (siehe unten).
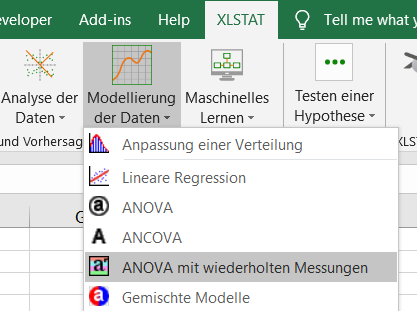
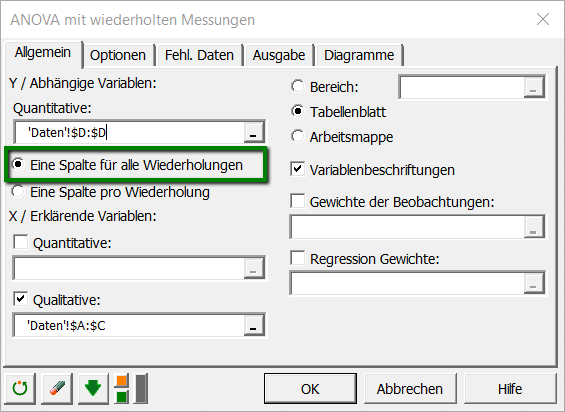
Nach dem Klicken des Buttons, erscheint das Dialogfenster der ANOVA mit wiederholten Messungen. Wählen Sie nun die Daten, die den zu berücksichtigenden Variablen entsprechen auf dem Excel-Blatt aus. Die „abhängigen Daten“ (oder zu modellierende Variable) ist hier die Spalte „Dp“. Unser Ziel ist es den Effekt der Gruppe, der Zeit und der Interaktion beider auf die Variabilität des Depressionspotential zu bestimmen. Da die Spaltennamen für die Variablen ausgewählt wurden, aktivieren Sie bitte die Option „Beschriftung der Variablen“. Wählen Sie anschließend die wiederholten und Subjektfaktoren als erklärende Variablen.
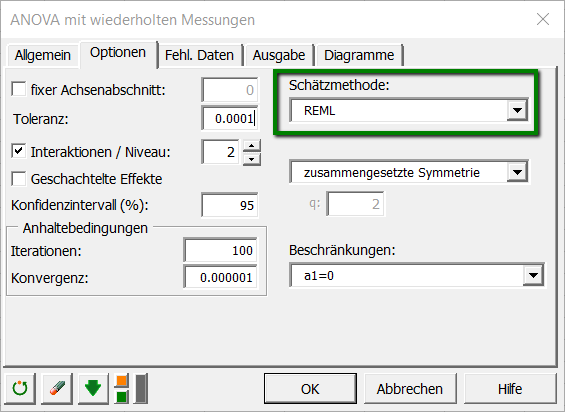
Im Reiter Optionen, aktivieren Sie die Option „Interaktionen“ und setzen Sie das maximale Interaktionsniveau auf 2. Lassen Sie die Beschränkungsoption bei "a1=0", was bedeutet, dass ein Modell mit der ersten Modalität der Variablen Gruppe (hier „Kontrolle“) als Standardeffekt für den Score erstellt wird. Obwohl Sie aus theoretischen Gründen eine Beschränkung anwenden müssen, hat diese keine Auswirkung auf die Ergebnisse (wie die Anpassungsgüte) des Modells. Der einzige Unterschied liegt in der Modellschreibweise. Die Kovarianzstruktur wird als Vorgabewert der zusammengesetzten Symmetrie gewählt.
Nach dem Klicken auf den OK Button, wird ein Dialogfenster zur Auswahl der Faktoren die im Modell zu berücksichtigen sind angezeigt. Die fixen Effekte sind die Zeit, Gruppe und Zeit*Gruppe, der wiederholte Faktor ist die Zeit und der Subjektfaktor ist Subjekt.
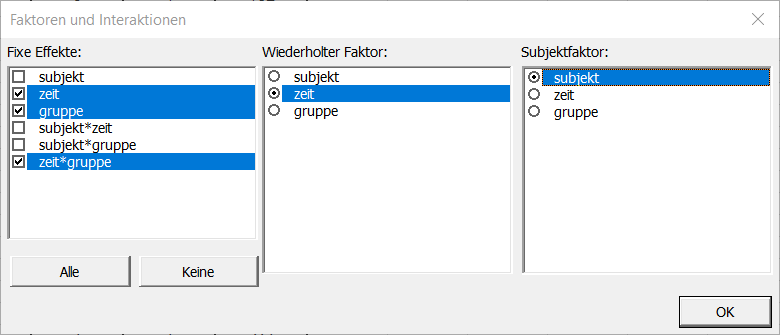
Bemerkung: Ein Faktor kann nicht Subjektfaktor und fixer Faktor gleichzeitig sein. Wiederholte und Subjektfaktoren müssen unterschiedlich sein und in beiden Fällen qualitativer Natur sein.
Nach dem Klicken auf den OK Button, beginnen die Berechnungen und die Ergebnisse werden auf einem neuen Excel-Blatt angezeigt.
Interpretieren der Ergebnisse einer ANOVA mit wiederholten Messungen anhand der gemischten Modelle
Die erste Tabelle zeigt die Koeffizienten der Anpassungsgüte des Modells an.

Die Modellparameter werden mittels der beschränkten Methode der maximalen Wahrscheinlichkeit (REML) ermittelt und sind unterschiedlich im Vergleich zu einer klassischen ANOVA. Alle Indizes werden benutzt, um Modelle mit verschiedener Kovarianzstruktur zu vergleichen.
In der nächsten Tabelle werden die Kovarianzparameter zusammen mit dem zugehörigen Z Test angezeigt. Man kann erkennen, dass beide Parameter signifikant sind.
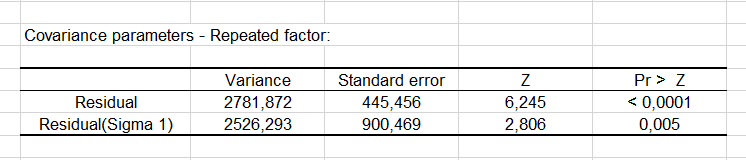
Es werden ebenfalls die modellverursachte Kovarianz- und Korrelationsmatrix angezeigt werden.
Der Test der Nullmodellwahrscheinlichkeit vergleicht die beiden Modelle die durch die ausgewählte Kovarianzstruktur und durch eine klassische diagonale Kovarianzstruktur erhalten werden. Der erhaltene p-value kann zur Beurteilung der Signifikanz der Modellanpassung gebraucht werden. 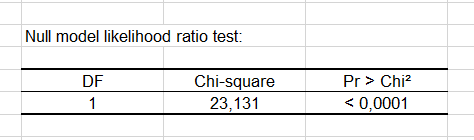
Mann kann sehen, dass die Auswahl der zusammengesetzten Symmetrie einen positiven Effekt auf die Modellanpassung hat.
Der Typ III der fixen Effekte zeigt, dass alle Faktoren signifikante Effekte auf das Depressionspotential haben. Diese Tests sind sehr wichtig und ersetzen die Typ III SS des klassischen ANOVA-Modells.
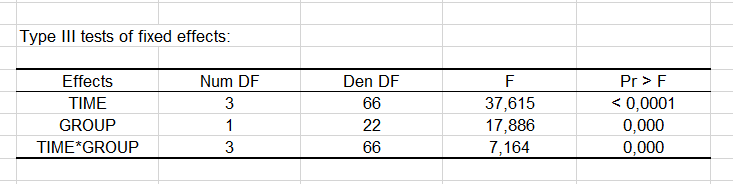
Anhand der angezeigten Ergebnisse der Typ III Tabelle, kann man sagen, dass die Variablen „Zeit“ den größten Einfluss auf das Modell hat. Betrachtet man die Modellparameter (siehe unten), so kann man feststellen, dass die Zeitwerte 1, 3 und 6 einen negativen Einfluss auf das Depressionspotential haben. Patienten sind weniger deprimiert, je weiter die Zeit fortschreitet. Teil der Gruppe „Behandlung“ zu sein, hat einen negativen Einfluss auf das Depressionspotential.
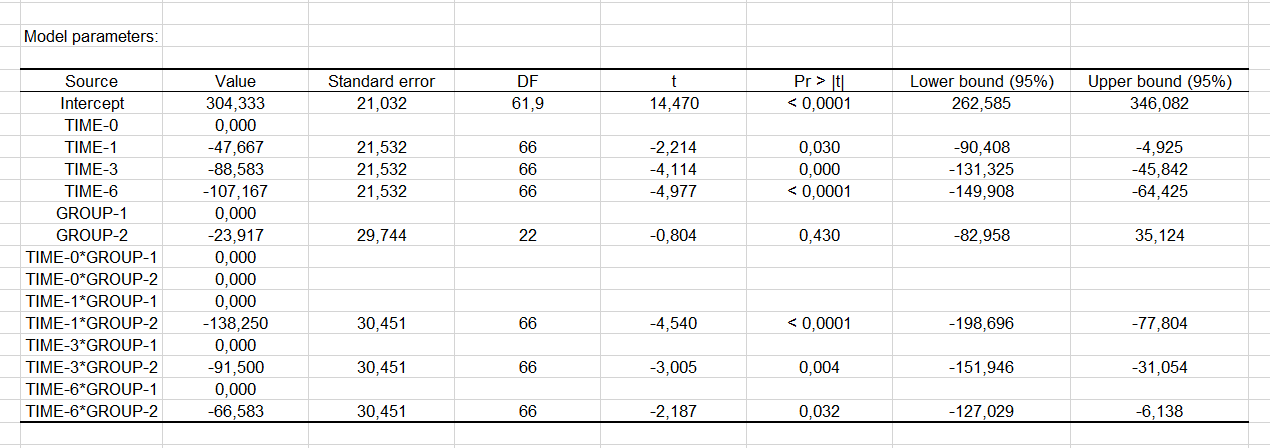
Die oben angezeigte Tabelle kann dazu verwendet werden, um den Einfluss der erklärenden Variablen auf das Depressionspotential und/oder um die durchschnittliche Veränderung in einer noch nicht vom Experiment abgedeckten Situation, wie im Fall des Zeitpunkt 6 für die „Behandlung“-Gruppe vorherzusagen. In diesem speziellen Beispiel, beträgt das durchschnittliche Depressionspotential 106.7, unter Berücksichtigung der Tatsache, dass der Einfluss der Interaktion ungewiss ist.
Diese Untersuchung hat gezeigt, dass sowohl Zeit als auch Behandlung einen signifikanten negativen Einfluss auf das Depressionspotential haben.
Weitere nützliche Ergebnisse sind in XLSTAT verfügbar, wie unter anderem die Residuen, die Residualdiagramme, die Diagramme der Quadratmittelwerte.
War dieser Artikel nützlich?
- Ja
- Nein