Paarweise Mehrfachvergleiche nach einer multiplen ANOVA

Dieses Tutorium wird Ihnen helfen, Vielfachvergleichsverfahren mit Anwendung im Kontext einer ANOVA (Analysis of Variance) mit zwei Faktoren in Excel mithilfe der Software XLSTAT besser zu verstehen.

Datensatz für die Durchführung paarweiser vielfacher Vergleiche nach einer multiplen ANOVA

Die Daten entsprechen einem sensorischen Test an 2 Lebensmittelprodukten. 4 Bewerter haben beide Produkte verkostet und vergaben Noten zu zwei Merkmalen: Geschmacksqualität und Süße. Jedes Produkt wurde 6 mal durch jeden Bewerter innerhalb verschiedener Verkostungssitzungen gekostet. Die Daten wurden künstlich generiert.

Absicht dieses Tutoriums

Die Absicht dieses Tutoriums besteht darin, sich auf mehrfache paarweise Vergleiche, auch genannt Post-hoc-Vergleiche, welche auch oft nach parametrischen oder nichtparametrischen Tests durchgeführt werden, zu konzentrieren. Wir untersuchen das Thema mit einem komplexen Beispiel, das zwei ANOVAs mit je zwei Faktoren beinhaltet, einschließlich der statistischen Interaktion mit zwei Faktoren Testperson x Produkt. Falls signifikant, spiegeln die Interaktion kontrastierende Unterschiede zwischen den Noten der beiden Produkte bei allen Testpersonen wider. Beispielsweise haben einige Testpersonen Produkt A höher bewertet als Produkt B, während andere Produkt B eine bessere Bewertung gaben als Produkt A. Mehrfache paarweise Vergleiche, die auf der Ebene der Interaktion durchgeführt wurden, könnten uns dabei helfen, genau zu bestimmen, welche Testperson zur ersten Gruppe und welche Testperson zur zweiten Gruppe gehört.

Einige Worte zu Tools für vielfache Vergleiche

Nach der Erkenntnis, dass ein Faktor global gesehen einen signifikanten Effekt auf eine abhängige Variable hat, möchten wir oft weiter ins Detail gehen und fragen, welche spezifischen Faktorstufen voneinander abweichen. Wir können beispielsweise die Effekte eines Faktors, der 4 medizinische Behandlungen umfasst, auf den Blutdruck testen. Die Durchführung einer ANOVA mit einem Faktor an den Daten würde folgende allgemeine Frage beantworten: „Gibt es mindestens eine Behandlung, die sich signifikant von den anderen unterscheidet?“ Wenn der ANOVA-Test signifikant ist, könnte eine weitere Frage gestellt werden: „Welche Behandlungen weichen voneinander ab?“ Für diese Frage ist es erforderlich, die Unterschiede zwischen allen Paaren von Behandlungen zu testen. Tools für paarweise vielfache Vergleiche wurden zur Behandlung dieses Problems entwickelt.

Tools für vielfache Vergleiche implizieren normalerweise die Berechnung eines p-Werts für jedes Paar von verglichenen Stufen. Der p-Wert stellt das Risiko dar, das wir eingehen, falsch zu liegen, wenn wir behaupten, dass ein Effekt statistisch signifikant ist. Je mehr Paare wir vergleichen möchten, desto höher ist die Zahl der berechneten p-Werte und demzufolge das Risiko, signifikante Effekte zu entdecken, die in der Realität nicht signifikant sind. Unter Berücksichtigung eines Signifikanzniveaus alpha von 5 % würden wir wahrscheinlich zufällig 5 signifikante p-Werte gegenüber 100 untersuchten Auswirkungen, die in der Realität nicht signifikant sind, finden. Demzufolge umfassen Tools für mehrfache paarweise Vergleiche p-Wert- Korrekturen: p Werte werden mit zunehmender Anzahl penalisiert (angehoben).

Die Wahl der Paare von Faktorstufen, die zu vergleichen sind, hängt von unserer Fragestellung ab und sollte somit während der Planung der Studie erfolgen. Tatsächlich interessieren wir uns oft für den Vergleich aller Stufen miteinander. In diesem Zusammenhang bietet XLSTAT verschiedene Methoden, einschließlich des Tukey-HSD-Verfahrens (Tukey Honest Significant Difference), das neben Fisher LSD eines der am häufigsten verwendeten Verfahren bei paarweisen vielfachen Vergleichen ist. Die Newman-Keuls-SNK-Methode ist ebenfalls berühmt und steht in XLSTAT zur Verfügung, obwohl sie aufgrund ihrer schwach konservativen Struktur nicht sehr zuverlässig ist. Die REGWQ-Methode zählt zu den zuverlässigsten Tests, obwohl sie nicht häufig verwendet wird.

In anderen Situationen möchten wir nur jede Stufe mit einem Kontrollwert zu vergleichen. Durch die Wahl dieser Untergruppe von Paaren nimmt die Anzahl der berechneten p-Werte ab und nachfolgend ihre Penalisierung. In diesem Fall sprechen wir von Dunnett-Kontrasten, die ebenfalls in XLSTAT zur Verfügung stehen. Stärker personalisierte Paare können auch über Kontraste spezifiziert werden.

Bevor wir mit diesem Tutorium fortfahren, sollten Sie einen Blick auf einen sehr einfachen Fall von vielfachen Vergleichen nach einer ANOVA mit einem Faktor in XLSTAT werfen.

Durchführung paarweiser vielfacher Vergleiche nach ANOVAs mit zwei Faktoren

Wir führen paarweise vielfache Vergleiche nach zwei ANOVAs mit je zwei Faktoren einschließlich einer Interaktion zwischen den Faktoren durch.

Öffnen Sie das XLSTAT-Menü und klicken Sie auf XLSTAT-Modellierung der Daten/ANOVA. In der Registerkarte Allgemein wählen Sie die Spalten Geschmack und Süße als abhängige Variablen und die Spalten Testperson und Produkt als erklärende, qualitative Variablen aus. In der Registerkarte Optionen aktivieren Sie die Option Interaktionen/Niveaus und wählen Sie Interaktionen auf 2 Niveaus, sodass die statistische Interaktion Testperson x Produkt berücksichtigt wird. Achten Sie darauf, dass Sie in der Registerkarte Ausgabe/Allgemein die Option Typ I/II/III SS aktivieren.

In der Registerkarte vielfache Vergleiche aktivieren Sie die Option Paarweise Vergleiche und wählen Sie danach Tukey HSD. Durch die Aktivierung der Optionen Standardfehler und Konfidenzintervalle in dieser Registerkarte werden diese Funktionen um die Mittelwerte berechnet und in den Ergebnissen angezeigt. Wird die Option „Anwenden auf alle Faktoren“ nicht aktiviert, können Sie Modellfaktoren und/oder Interaktionen auswählen, für die Sie vielfache Vergleiche durchführen möchten. Klicken Sie auf den Button OK.

Nach dem Klicken des entsprechenden Buttons erscheinen nacheinander drei Dialogfenster. Im ersten müssen Sie definieren, welche Gruppe von Faktoren und Interaktionen Sie in die allgemeinen ANOVA-Modelle integrieren möchten. In den beiden folgenden müssen Sie die Gruppe von Faktoren und Interaktionen definieren, für die Sie mehrfache paarweise Vergleiche für jede der beiden abhängigen Variablen durchführen möchten. Wählen Sie die drei Elemente der Liste (zwei Faktoren und eine Interaktion) in allen drei Dialogfenstern aus.

Die Ergebnisse werden dann in einer neuen Excel-Mappe angezeigt.

Interpretieren paarweiser vielfacher Vergleiche nach ANOVAs mit zwei Faktoren

Für die Geschmacksvariable sind die drei ANOVA-Tabellen mit der Summe der Quadratwerte genau identisch. Dieser Fall tritt bei einem ausgeglichenen Versuchsplan ein. Ist der Plan unausgeglichen, ist die Tabelle mit der Summe der Quadratwerte vom Typ III die zuverlässigste (sehen Sie sich dieses Tutorium an). Obwohl der Produkteffekt auf den Geschmack mit 0,05 nicht signifikant ist (p-Wert = 0,334), ist die statistische Interaktion Testperson x Produkt sehr signifikant (p-wert < 0,0001).

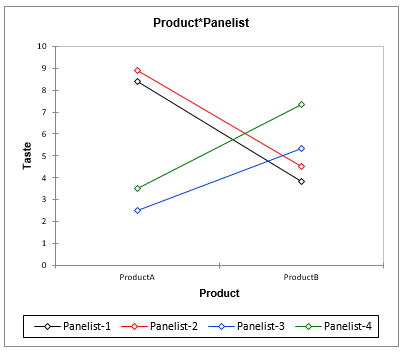
Die Interpretation dieses Musters erfolgt ganz einfach durch Verwendung des Mittelwert-Diagramms unten rechts: Obwohl durchschnittlich beide Produkte auf der Geschmacksskala fast identisch bewertet werden (ca. 5,5), haben die Testpersonen anscheinend sehr kontrastierende Ansichten. Während die Testpersonen 1 und 2 Produkt A gegenüber Produkt B stark bevorzugen, bevorzugen die Testpersonen 3 und 4 Produkt B gegenüber Produkt A. Darüber hinaus stimmen anscheinend alle Testpersonen mit einer durchschnittlichen Geschmacksbewertung für Produkt B überein.

Konzentrieren wir uns nun auf den Bereich paarweise vielfache Vergleiche. Jeder Faktor oder jede Interaktion hat einen eigenen Unterbereich. Für den Faktor Testperson werden alle Testpersonen ungeachtet des Produkts miteinander verglichen. Für den Faktor Produkt werden beide Produkte ungeachtet der Testpersonen miteinander verglichen. Für die Interaktion Testperson x Produkt werden alle Kombinationen von Niveaus zwischen den beiden Faktoren miteinander verglichen. Gewöhnlich ist es interessant, auf Faktoren oder Interaktionen zu achten, die gemäß der ANOVA-Tabelle am signifikantesten sind. Aus diesem Grund sehen wir uns die Interaktionsgröße für die Geschmacksvariable genauer an.

Zuerst wird eine Tabelle angezeigt, die umfassende Informationen wie durchschnittliche Differenzen und korrigierte p-Werte für jedes Paar enthält.

Die Signifikanzinformationen, die sich aus dieser Tabelle ergeben, werden nachstehend in einer kleineren Tabelle zusammengefasst, in der die Kombinationen zwischen den Niveaus der beiden Faktoren Buchstaben zugeordnet sind. Bei der Interpretation konzentrieren wir uns auf diese zweite Tabelle.

Zwei Niveaukombinationen mit demselben Buchstaben sind nicht signifikant unterschiedlich. Zwei Kombinationen, die keinen Buchstaben gemeinsam haben, unterscheiden sich signifikant.

Global gesehen werden die Schlussfolgerungen, die wir aus den Grafiken der Mittelwerte gezogen haben, durch die Tabellen der paarweisen vielfachen Vergleiche statistisch unterstützt.

In Kombinationen, die Produkt A beinhalten (die ersten und letzten beiden Zeilen der Tabelle), teilen Testperson 1 und 2 denselben Buchstaben (A) und haben keinen Buchstaben mit Testperson 3 und 4 gemeinsam, die ebenfalls denselben Buchstaben (C) teilen. Das bedeutet, dass die beiden Gruppen von Testpersonen bei Produkt A nicht übereinstimmen. In Kombinationen, die Produkt B beinhalten (die 4 mittleren Zeilen der Tabelle), haben alle Kombinationen den Buchstaben B. Das bedeutet, dass alle Testpersonen in Bezug auf den Geschmack von Produkt B übereinstimmen.

Aus Marketingsicht wäre es interessant beim Bewerben von Produkt A Verbraucher, deren Profil Testperson 1 und 2 ähnelt, als Zielgruppe zu nehmen. Andererseits könnte Produkt B eine gewisse Geschmacksverbesserung vertragen, bevor in Erwägung gezogen wird, es auf den Markt zu bringen.

Für die abhängige Variable Süße zeigen die ANOVA-Tabellen einen sehr signifikanten Effekt des Produkts (p-Wert < 0,0001) und nicht signifikante Effekte der Testperson (p-Wert = 0,704) und Interaktion (p-wert = 0,427).

Die Grafik der Mittelwerte unten rechts zeigt, dass alle Testpersonen in der Tatsache übereinstimmen, dass Produkt B süßer ist als Produkt A.

Es wäre trivial, hier den Bereich der vielfachen Vergleiche zu untersuchen, da das einzige signifikante Element des Modells (d. h. der Produktfaktor) zwei Niveaus enthält, welche sich zwangsläufig von den Aussagen der ANOVA-Tabellen unterscheiden werden.

Interpretieren der Diagramme der Mittelwertschätzer

Wir haben die interaktiven Effekte von Testperson und Produkt sowohl auf die abhängigen Variablen Geschmack als auch Süße getestet. XLSTAT bietet ein Tool für Mittelwertschätzer, das für den Vergleicht der Effekte derselben Gruppe von Faktoren und Interaktionen auf verschiedene abhängige Variablen nützlich ist.

Eine zusammenfassende Tabelle der Mittelwertschätzer sowie ein Diagramm der Mittelwertschätzer ist jedem Faktor und jeder Interaktion zugeordnet.

Für den Faktor Testperson zeigt die zusammenfassende Tabelle der Mittelwertschätzer Schätzungen der durchschnittlichen Bewertung jeder Testperson für die beiden abhängigen Variablen an. Beachten Sie, dass innerhalb jeder abhängigen Variable Buchstaben für die Signifikanz paarweiser vielfacher Vergleiche als Kommentare innerhalb der Zellen mit Schätzungen der Mittelwerte eingeführt werden. Um die Buchstaben anzuzeigen, die einem bestimmten Mittelwert zugeordnet sind, bewegen Sie einfach den Mauszeiger auf das rote Dreieck in der oberen rechten Ecke der entsprechenden Zelle.

Das Diagramm zeigt, dass unabhängig von den Produkten Testpersonen meistens in Bezug auf den Geschmack nicht übereinstimmen, dafür aber in Bezug auf die Süße übereinstimmen, was durch p-Werte unterstützt wird, die mit den Effekten der Testpersonen in beiden ANOVA-Modellen verknüpft sind.

Das Diagramm der Mittelwertschätzer für das Produkt zeigt, dass unabhängig von der Testperson die Produkte im Durchschnitt auf der Geschmacksskala gleich bewertet werden, während sie auf der Süße-Skala unterschiedlich beurteilt werden.

Wir werden das Diagramm für die Interaktion der Mittelwertschätzer nicht analysieren, da es zu verwirrend ist.