Comparaisons multiples suite à des ANOVAs à plusieurs facteurs

Ce tutoriel explique comment mettre en place et interpréter une comparaison multiples par paires suite à des ANOVAs à plusieurs facteurs dans Excel avec XLSTAT.

Jeu de données pour la réalisation de comparaisons multiples par paires suite à des ANOVAs à plusieurs facteurs

Les données correspondent à un test sensoriel de deux produits alimentaires. 4 juges ont testé les deux produits et évalué numériquement deux caractéristiques : qualité du goût et douceur. Chaque produit a été testé 6 fois par chaque juge sur différentes sessions. Les données ont été simulées artificiellement.

But de ce tutoriel

L’objectif de ce tutoriel est de faire une mise au point sur la notion de comparaisons multiples par paires, aussi appelées comparaisons post hoc, souvent effectuées à la suite de tests paramétriques ou non paramétriques. Nous abordons cette notion au travers d’un exemple poussé impliquant des ANOVAs à deux facteurs avec effet d’interaction juge x produit. Si elle est significative, cette interaction pourrait refléter des écarts d’évaluation entre le produit X et le produit Y changeant significativement en fonction du juge. Si c’est le cas, les comparaisons multiples par paires effectuées à ce niveau d’interaction permettront d’identifier les juges qui auront attribué une meilleure note au produit X par rapport au produit Y et inversement.

Quelques mots sur les outils de comparaisons multiples

Après avoir détecté un effet significatif d’un facteur sur une variable dépendante, il est souvent intéressant d’aller plus loin en se demandant quelles modalités spécifiques du facteur diffèrent significativement Par exemple, dans le cadre d’une étude visant à tester l’effet d’un facteur impliquant 4 traitements médicaux sur la pression artérielle, un test d’ANOVA répondrait à la question très générale : « existe-t-il au moins un traitement différant significativement des autres ? » Si le test d’ANOVA se solde par un effet significatif, une autre question peut être soulevée : « quels traitements précis sont significativement différents l’un de l’autre ? » Cette question exige la mise en œuvre de tests de différences entre toutes les paires de traitements pris deux à deux. Les outils de comparaisons multiples par paires ont été développés dans cette perspective.

Les outils de comparaisons multiples par paires impliquent généralement le calcul d’une p-value pour chaque paire de modalités comparées. La p-value représente le risque que l’on prend de se tromper en affirmant qu’un effet est statistiquement significatif. Plus le nombre de paires à comparer augmente, plus le nombre de p-values calculées augmente, entraînant par conséquent une amplification du risque de déclarer des effets significatifs à tort. En considérant un seuil de significativité de 5%, on trouverait 5 p-values significatives par pur hasard sur 100 effets calculés et non-significatifs en réalité. Les outils de comparaisons multiples par paires mettent en jeu des corrections de p-values : ces dernières sont pénalisées ( = leurs valeurs sont augmentées) à mesure que leur nombre s’accroît.

Le choix de paires de modalités de facteurs à être comparés est intimement lié à la question posée à l’origine et doit ainsi être fait lors de la planification de l’étude. Nous sommes souvent intéressés par les comparaisons de toutes les modalités deux à deux. Dans cette perspective, XLSTAT propose différentes méthodes, notamment les procédures de Tukey HSD (Tukey Honest significant difference) et Fisher LSD, utilisées couramment. La méthode SNK de Newman-Keuls est également très populaire et disponible dans XLSTAT, mais peu recommandée car peu conservative. La méthode REGWQ fait partie des méthodes les plus fiables, cependant elle est très peu utilisée.

Dans d’autres situations, nous sommes uniquement intéressés par la comparaison de chaque modalité avec une modalité témoin. En sélectionnant un sous-ensemble de paires de modalités à comparer, nous diminuons le nombre de p-values calculées et par conséquent la sévérité de leur pénalisation. Dans ce cas, il est question de contrastes de Dunnett, également disponibles dans XLSTAT. Un choix de paires plus personnalisé peut être spécifié à travers l'analyse de contrastes.

Avant de passer à la suite de ce tutoriel, vous pouvez jeter un coup d’œil sur un cas très simple de comparaisons multiples à la suite d’une ANOVA à un facteur avec XLSTAT.

Réaliser des comparaisons multiples par paires à la suite d’ANOVAs à deux facteurs

Nous effectuerons des tests de comparaisons multiples par paires à la suite de deux ANOVAs à deux facteurs impliquant une interaction entre les deux facteurs.

Ouvrez le menu XLSTAT, puis cliquez sur XLSTAT-Modélisation des données / ANOVA. 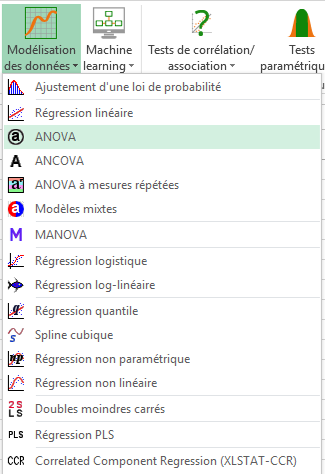Dans l’onglet Général, sélectionner les colonnes goût et douceur en guise de variables dépendantes, et les colonnes juge et produit en tant que variables explicatives qualitatives. Dans l’onglet Options, activez l’option Interactions / niveau et sélectionnez des interactions à 2 niveaux afin que l’interaction juge x produit soit prise en compte. Dans l’onglet Sorties / Général, activez l’option Type I/II/III SS.

Dans l’onglet Comparaisons multiples, activez l’option comparaisons par paires, puis choisissez Tukey HSD. So vous activez les options erreurs standard et intervalle de confiance, XLSTAT calculera ces statistiques autour des moyennes et les affichera dans les résultats. Si l’option « Appliquer à tous les facteurs » n’est pas activée, vous pourrez choisir les facteurs et/ou interactions du modèle sur lesquels vous désirez réaliser des tests de comparaisons multiples. Cliquez sur le bouton OK.

Une fois le bouton cliqué, trois boîtes de dialogue apparaissent successivement. Dans la première, vous devez identifier l’ensemble de facteurs et d’interactions que vous désirez inclure dans les modèles ANOVA globaux. Dans les deux boîtes qui suivent, vous devez définir l’ensemble des facteurs et d’interactions sur lesquels vous désirez qu’XLSTAT réalise des comparaisons multiples par paires pour chacune des deux variables dépendantes, respectivement. Sélectionnez les trois éléments de la liste (deux facteurs et une interaction) au sein des trois boîtes de dialogue.

Les résultats apparaissent au sein d’une nouvelle feuille de calcul Excel.

Interprétation de comparaisons multiples par paires à la suite d’ANOVAs à 2 facteurs

Pour la variable goût, les trois types d’ANOVA fournissent des résultats strictement identiques. Ceci se produit lorsque le dispositif expérimental est parfaitement équilibré. Si le dispositif n’est pas équilibré, il vaut mieux se fier à l’analyse de type III (voir ce tutoriel). Malgré le fait que l’effet produit ne soit pas significatif au seuil de 5% (p-value = 0.334), l’interaction juge x produit est très significative (p-value < 0.0001).

Ce résultat peut facilement être interprété grâce au graphique des moyennes situé en bas à droite : les deux produits ont reçu en moyenne la même évaluation au niveau de la qualité de goût (5.5 environ). Cependant, les juges ne semblent pas du tout être d’accord entre eux. Alors que les juges 1 et 2 préfèrent largement le produit X par rapport au produit Y, les juges 3 et 4 préfèrent le produit Y par rapport au produit X. Enfin, tous les juges semblent plutôt d’accord sur un goût relativement moyen du produit Y.

Focalisons-nous à présent sur les comparaisons multiples par paire. Chaque facteur ou interaction engendre une analyse qui lui est propre. L’analyse du facteur juges implique une comparaison de tous les juges les uns avec les autres sans tenir compte d’un effet produit. L’analyse du facteur produit implique une comparaison de tous les produits les uns avec les autres sans tenir compte d’un effet juge. Enfin, l’analyse de l’interaction juge x produit implique les comparaisons de toutes les combinaisons possibles de modalités des deux facteurs. En général, on accorde plus d’importance aux facteurs ou interactions les plus significatifs au sein de la table d’ANOVA. Nous nous focaliserons donc sur les analyses relatives à l’effet d’interaction.

Un premier tableau affiche des informations détaillées sur chaque paire, notamment les différences de moyennes ainsi que les p-values pénalisées et les significativités associées.

L’information relative aux significativités est ensuite résumée au sein d’un plus petit tableau, où chaque combinaison de modalités entre les deux facteurs est associée à une ou plusieurs lettres. Nous centrerons notre interprétation sur ce tableau.

Deux combinaisons de modalités partageant la même lettre ne sont pas significativement différentes. Deux combinaisons n’ayant aucune lettre en commun sont significativement différentes.

Globalement, les conclusions auxquelles nous avons abouti via le graphique des moyennes sont appuyées statistiquement par les tableaux relatifs aux comparaisons multiples.

Dans les combinaisons de modalités de facteurs impliquant le produit X (premières deux lignes et dernières deux lignes du tableau), les juges 1 et 2 partagent la même lettre (A) et n’ont aucune lettre en commun avec les juges 3 et 4 qui, eux, partagent la lettre C. Ceci signifie que les deux groupes de juges sont en désaccord en ce qui concerne le produit X. Dans les combinaisons contenant le produit Y (4 lignes centrales dans le tableau), toutes les combinaisons partagent la lettre B. Ceci signifie que tous les juges sont d’accord sur le goût du produit Y.

Dans une stratégie de marketing, il serait intéressant de cibler des consommateurs ayant des profils similaires aux juges 1 et 2 dans les campagnes publicitaires pour le produit X. D’un autre côté, le produit Y devrait peut-être subir une amélioration au niveau du goût avant d’être mis sur le marché.

Pour la variable douceur, les tables d’ANOVA montrent un effet très significatif du produit (p-value < 0.0001) et non-significatif du le facteur juge (p-value = 0.704) et de l’interaction (p-value = 0.427).

Le graphique des moyennes situé en bas à droite montre que tous les juges semblent d’accord sur le fait que le produit Y est plus sucré que le produit X.

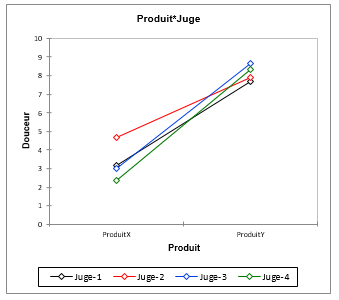
Il n’est pas nécessaire d’examiner les analyses de comparaisons multiples par paires ici, car le seul facteur significatif (effet produit) ne comprend que deux modalités, qui sont nécessairement différentes comme suggéré par la table d’ANOVA.

Interprétation des synthèses « moyennes estimées » sur toutes les variables dépendantes

Nous avons testé les effets interactifs entre juge et produit sur la qualité du goût et sur la douceur. XLSTAT produit des résultats synthétiques permettant de comparer les effets d’un même ensemble de facteurs et d’interactions sur plusieurs variables dépendantes (variables « Y », à ne pas confondre avec la modalité produitY).

Un tableau et un graphique synthétiques représentant les moyennes estimées sont fournis pour chaque facteur et chaque interaction.

Pour le facteur juge, le tableau affiche des estimations de la moyenne de l’évaluation de chaque juge pour chacune des deux variables dépendantes. Notez que les lettres associées aux comparaisons multiples par paires sont fournies sous formes de commentaires au sein des cellules contenant les estimations des moyennes. Afin d’afficher la (ou les) lettre(s) associée(s) à une moyenne spécifique, faites glisser le curseur de la souris sur le triangle rouge situé en haut à droite de la cellule correspondante.

Le graphique montre que, quel que soit le produit, les juges ont tendance à ne pas être d’accord sur la qualité de goût, mais sont globalement d’accord sur la douceur. Ces résultats sont appuyés par les p-values associées à l’effet juge au sein des tables d’ANOVA.

Le graphique associé à la synthèse relative à l’effet produit montre que les produits sont notés de la même manière en moyenne au niveau du goût, mais notés différemment au niveau de la douceur.