¿Qué es el modelado estadístico?
¿Qué es el modelado estadístico?
En términos sencillos, el modelado estadístico es una forma simplificada, matemáticamente formalizada, de aproximarse a la realidad (i.e., la que genera los datos) y, opcionalmente, hacer predicciones a partir de dicha aproximación.
Veamos un ejemplo básico. Supongamos que deseamos informar sobre el peso de una variedad de patatas. Podemos considerar una forma difícil y otra fácil de hacerlo. La difícil consiste en emplear años midiendo el peso de cada patata de esta variedad a lo largo del mungo, y trasladar los datos a una hoja Excel interminable. La fácil, consiste en seleccionar 30 patatas ampliamente representativas de la variedad que nos interesa, calcular su media y su desviación estándar, e informar únicamente sobre esas magnitudes como una descripción aproximada del peso. Representar una cantidad por una media y una desviación estándar es una forma muy simple de modelado estadístico.
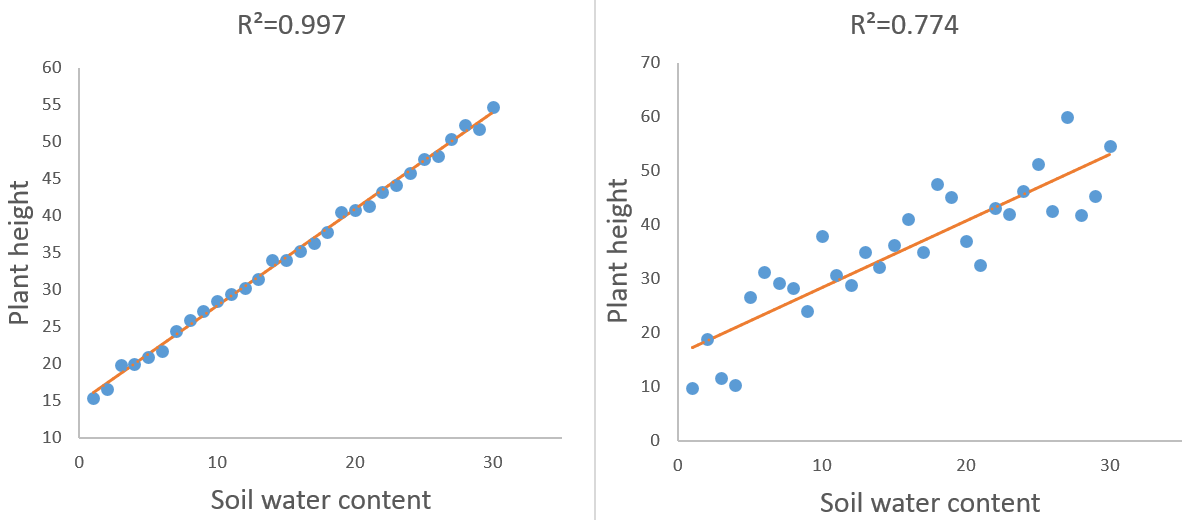
Otro ejemplo es intentar representar la altura de las plantas en función del agua del suelo mediante una línea recta caracterizada por una pendiente y una intercepción, trazada después de realizar un experimento sobre una muestra de plantas sometidas a una humedad del suelo creciente. Este modelo particular se denomina regresión lineal simple.

¿Qué son variables dependientes y explicativas?
En la mayoría de los casos, los modelos estadísticos implican variables explicativas y variables dependientes. La variable dependiente es aquella que queremos describir, explicar, o predecir. Como norma general, la variable dependiente es la representada en el eje Y en los gráficos. En el ejemplo de la altura de las plantas, la variable dependiente es la altura de la planta. Las variables explicativas, también denominadas variables independientes, son aquellas que usamos para explicar, describir o predecir la(s) variable(s) dependiente(s). Las variables explicativas generalmente se representan en el eje X. En el ejemplo de la altura de las plantas solo usamos una variable independiente cuantitativa (el contenido en agua del suelo). Tanto las variables dependientes como las explicativas pueden ser una o varias, cuantitativas o cualitativas. Se han desarrollado modelos adaptados a las diferentes situaciones.
¿Qué es un parámetro de un modelo?
En los modelos clásicos, paramétricos, la(s) variable(s) dependiente(s) está vinculada a las explicativas a través de una ecuación matemática (el modelo) que implica cantidades denominadas parámetros del modelo. En el ejemplo de la altura de las plantas (regresión lineal simple) los parámetros son la intercepción y la pendiente. La ecuación puede representarse así: Altura = intercepción + pendiente*contenido en agua del suelo Los cálculos que subyacen al modelado estadístico permiten la estimación de los parámetros del modelo, así como ulteriores predicciones de la variable dependiente. 1La regresión lineal simple implica también un tercer parámetro, la varianza de los residuos (vid. párrafo siguiente).
¿Qué es un residuo de un modelo?
Técnicamente, los residuos (o errores) de un modelo son las distancias entre los puntos que representan los datos y el modelo (que está representado por una línea recta en el ejemplo de regresión lineal simple de la altura de las plantas).

Los residuos del modelo representan la parte de variabilidad de los datos que el modelo ha sido incapaz de capturar. El estadístico R² es la parte de variabilidad que es explicada por el modelo. Así, mientras más pequeños sean los residuos, mayor será el estadístico R².
¿Qué modelo estadístico debería elegir?
Esta tabla le guiará en la elección de los modelos más frecuentemente usados de acuerdo al tipo y número de variables dependientes e independientes. También se proponen soluciones distintas a los modelos paramétricos.
¿Ha sido útil este artículo?
- Sí
- No