¿Cuál es la diferencia entre pruebas paramétricas y no paramétricas?

¿Cuál es la diferencia entre pruebas paramétricas y no paramétricas?

Las pruebas paramétricas asumen distribuciones estadísticas subyacentes a los datos. Por tanto, deben cumplirse algunas condiciones de validez, de modo que el resultado de la prueba paramétrica sea fiable. Por ejemplo, la prueba t de Student para dos muestras independientes será fiable solo si cada muestra se ajusta a una distribución normal y si las varianzas son homogéneas.

Las pruebas no paramétricas no dehen ajustarse a ninguna distribución. Pueden por tanto aplicarse incluso aunque no se cumplan las condiciones de validez paramétricas.

Las pruebas paramétricas tienen muchas veces sus equivalentes no paramétricas. Encontrará las diferentes pruebas paramétricas junto con sus equivalentes (en el caso de que existan) en esta tabla.

¿Cuál es la ventaja de usar una prueba no paramétrica?

Las pruebas no paramétricas son más robustas que las paramétricas. En otras palabras, son válidas en un rango más amplio de situaciones (exigen menos condiciones de validez).

¿Cuál es la ventaja de usar una prueba paramétrica?

La ventaja de usar una prueba paramétrica en lugar de una no paramétrica consiste en que la primera tiene más potencia estadística que la segunda. En otras palabras, una prueba paramétrica tiene mayor capacidad para conducir a un rechazo de H0. La mayoría de las veces, el valor p asociado a una prueba paramétrica es menor que el valor p asociado a su equivalente no paramétrica ejecutada sobre los mismos datos.

¿Cómo puedo utilizar pruebas paramétricas y no paramétricas en XLSTAT?

XLSTAT ofrece la mejor manera de generar pruebas paramétricas o no paramétricas en todas las soluciones, incluso la Basic. La mayoría de las pruebas paramétricas tienen un equivalente no paramétrico para realizar los mismos análisis, independientemente de las distribuciones estadísticas en sus datos. En la tabla de equivalencia que sigue, puedes ver varias pruebas contenidas en nuestro programa.

¿Para qué la usamos?	Prueba paramétrica	Prueba no paramétrica
Comparar una media observada con una teórica	Prueba t para una muestra	Prueba de los rangos con signo de Wilcoxon
Comparar dos medias independientes	Prueba t para dos muestras independientes	Prueba de Mann-Whitney
Comparar varias medias independientes	ANOVA	Prueba de Kruskal-Wallis/prueba de Mood
Comparar dos medias observadas dependientes	Prueba t para dos muestras dependientes	Prueba de Wilcoxon
Comparar varias medias observadas dependientes	ANOVA de medidas repetidas, modelos mixtos	Prueba de Friedman / Prueba de Durbin Skilling-Mack, Prueba de Page
Probar la asociación entre dos variables cualitativas	Chi-cuadrado sobre tabla de contingencia	Prueba Exacta de Fisher ; método Monte Carlo
Probar la asociación entre dos variables cuantitativas	Prueba de correlacion de Pearson	Prueba de correlacion de Spearman
Comprobar la existencia de valores atípicos (outliers)	Prueba de Dixon / Prueba de Grubbs	Gráfico de cajas (boxplot ) (no es una prueba)

Por ejemplo, si quiere comparar una media observada con una media teórica:

• ¿Necesita comparar la media de una clase con la media de la región? Vamos a utilizar una prueba paramétrica porque podemos suponer que los datos siguen una distribución normal. Tiene que elegir el t-test.

• ¿Necesita comparar el liking score mediano de una nueva marca de chips con la marca más apreciada del mercado?  No podemos suponer que los liking scores sigan una distribución normal entonces vamos a utilizar una prueba no paramétrica : la prueba de los rangos con signo de Wilcoxon.

Puede encontrar más precisiones sobre estos tests en este articulo.

¿Cómo puedo configurar una prueba paramétrica - no paramétrica en XLSTAT?

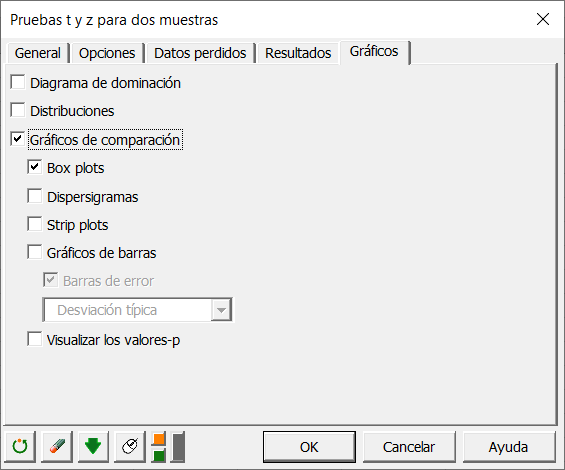
Es posible visualizar varias opciones en XLSTAT como Estadísticos descriptivos, intervalos de confidencia…

También puede visualizar varias tablas. Puede ver barras de error, los valores-p…