Quelle est la différence entre un test paramétrique et un test non-paramétrique ?

Quelle est la différence entre un test paramétrique et un test non-paramétrique ?

Les tests paramétriques se basent sur des distributions statistiques supposées dans les données. Par conséquent, certaines conditions de validité doivent être vérifiées pour que le résultat d’un test paramétrique soit fiable. Par exemple, le test t de Student pour échantillons indépendants n’est fiable que si les données associées à chaque échantillon suivent une distribution normale et si les variances des échantillons sont homogènes.

Les tests non-paramétriques ne se basent pas sur des distributions statistiques. Ils peuvent donc être utilisés même si les conditions de validité des tests paramétriques ne sont pas vérifiées.

Les tests paramétriques ont souvent des tests non-paramétriques équivalents. Vous trouverez une série de tests paramétriques courants ainsi que leurs équivalents non-paramétriques, lorsqu'ils existent, dans cette grille.

Quel est l'avantage d'utiliser un test non-paramétrique ?

Les tests non-paramétriques sont plus robustes que les tests paramétriques. En d'autres termes, ils peuvent être utilisés dans un plus grand nombre de situations.

Quel est l'avantage d'utiliser un test paramétrique ?

Les tests paramétriques sont, eux, plus puissants en général que leurs équivalents non-paramétriques. Autrement dit, un test paramétrique sera plus apte à aboutir à un rejet de H0, si ce rejet est justifié. La plupart du temps, la p-value calculée par un test paramétrique sera inférieure à la p-value calculée par un équivalent non-paramétrique exécuté sur les mêmes données.

A quoi sert-il ?	Test paramétrique	Test non paramétrique
Moyenne observée VS théoriques	Test t pour un échantillon	Test de Wilcoxon pour deux échantillons appariés
Comparer deux moyennes indépendantes	Test t de Student sur deux échantillons indépendants	Test de Mann-Whitney
Comparer plusieurs moyennes indépendantes	ANOVA	Test de Kruskal-Wallis test / Test de Mood
Comparer deux moyennes dépendantes observées	Test t de Student sur deux échantillons appariés	Test de Wilcoxon
Comparer plusieurs moyennes dépendantes observées	ANOVA à mesures répétées / modèles mixtes	Test de Friedman / Test de Durbin, Test de Skillings-Mack / Test de Page
Tester l'association entre deux variables qualitatives	Test du Khi2 sur tableau de contingence	Test exact de Fisher / Méthode de Monte Carlo method
Tester l'association entre deux variables quantitatives	Corrélation de Pearson	Corrélation de Spearman
Tester les valeurs extrêmes	Test de Dixon / Test de Grubbs	Boxplot (not really a test)

Par exemple, si vous voulez comparer une moyenne observée à une valeur théorique :

• Vous souhaitez comparer la moyenne des notes en mathématiques d'une classe à la moyenne du pays ? Dans ce cas nous allons utiliser un test paramétrique car nous pouvons supposer que les données suivent une distribution normale. Nous allons utiliser un test t de Student.

• Vous souhaitez comparer le score médian d'appréciation d'une nouvelle marque de chips à la marque la plus consommée du marché ? Nous ne pouvons pas supposer que les scores de préférence suivent une distribution normale, nous allons donc effectuer un test non paramétrique de rang signé de Wilcoxon à un échantillon.

Vous trouverez plus de précisions concernant nos tests dans cet article.

Comment mettre en place une analyse par test statistique paramétrique - non paramétrique dans XLSTAT ?

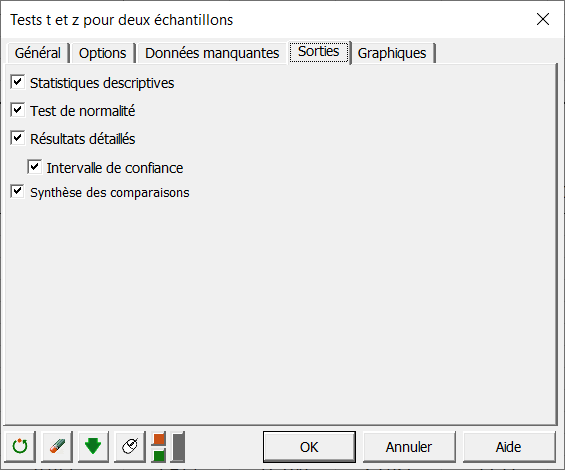
Vous pouvez personnaliser vos tests statistiques en utilisant les boîtes de dialogue de XLSTAT et afficher différents résultats tels que les statistiques descriptives, les intervalles de confiance...

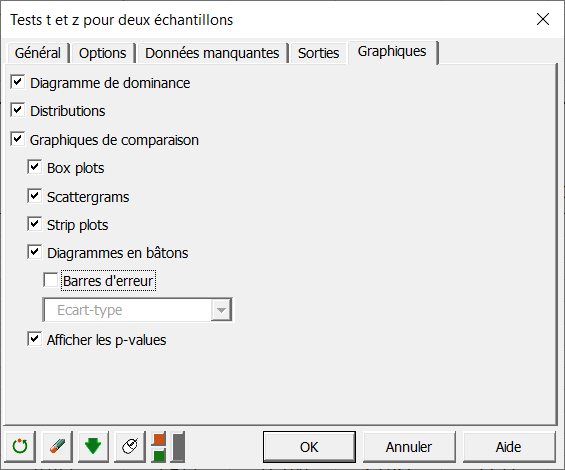
Vous pouvez également générer plusieurs graphiques. Vous pouvez choisir d'afficher les barres d'erreur, les p-values...