Taille d'échantillon et puissance pour une régression linéaire dans Excel
Ce tutoriel explique comment calculer et interpréter une taille d’échantillon et une puissance pour une régression linéaire avec Excel en utilisant XLSTAT.
Qu'est-ce que la puissance d'un test statistique ?
XLSTAT, dans son module Modélisation des données, propose un outil permettant d'appliquer un modèle de régression linéaire. XLSTAT permet d'estimer la puissance ou de calculer le nombre d'observations nécessaires associée aux variations du R² dans le cadre d'une régression linéaire.
Lorsqu'on teste une hypothèse à l'aide d'un test statistique, on a plusieurs éléments à choisir :
-
L'hypothèse nulle H0 et l'hypothèse alternative Ha.
-
Le test statistique à utiliser.
-
L'erreur de première espèce (erreur de type I) que l'on appelle aussi alpha. Elle se produit lorsqu'on rejette l'hypothèse nulle alors qu'elle est vraie. Elle est fixée a priori pour chaque test et vaut 5%.
L'erreur de seconde espèce ou beta est moins étudiée, mais elle revêt une grande importance. En effet, elle représente la probabilité que l'on ne rejette pas l'hypothèse nulle alors qu'elle est fausse. On ne peut pas la fixer a priori mais, on peut essayer de la minimiser, en jouant sur les autres paramètres du modèle. La puissance d'un test est calculée comme 1-beta et représente la probabilité que l'on rejette l'hypothèse nulle alors qu'elle est bien fausse.
On voudra donc maximiser la puissance du test. XLSTAT permet de calculer cette puissance (ainsi que beta) lorsque les autres paramètres du test sont connus. D'autre part, il permet pour une puissance donnée d'évaluer la taille de l'échantillon nécessaire à l'obtention de cette puissance.
Les calculs de puissance en statistique se font généralement avant que l'expérience ne soit menée. On s'en sert principalement pour estimer le nombre d'observations nécessaires pour que l'expérience ait la qualité statistique requise.
But de ce tutoriel
Dans une future étude, on désire étudier le poids d'enfants en fonction de la taille et de l'âge des enfants (comme dans le tutoriel sur la régression linéaire multiple). On veut donc savoir si le R² de ce modèle est significativement différent de 0.
On aura donc deux variables explicatives ou prédicteurs et on voudrait savoir combien d'enfants doivent être interrogés afin d'obtenir une puissance de 0,9. Comme nous ne connaissons pas encore les paramètres de nos échantillons, nous allons utiliser le concept de taille de l'effet (effect size). Cohen (1988) a introduit ce concept qui permet de donner un ordre de grandeur pour l'importance de l'effet. On testera donc 3 tailles d'effets : 0,02 pour un effet faible, 0,15 pour un effet modéré et 0,35 pour un effet fort. On s'attend à ce que plus la taille de l'effet est grande, plus la taille d'échantillon nécessaire sera petite.
Paramétrer le calcul de la taille de l'échantillon nécessaire dans le cadre d’une régression linéaire
Une fois XLSTAT lancé, cliquez sur l'icône Power et choisissez la fonction régression linéaire.
Une fois le bouton cliqué, la boîte de dialogue apparaît.
Vous devez alors choisir l'objectif Trouver la taille de l'échantillon, puis sélectionner le **test R² différent de 0.
L'alpha** est de 0,05. La puissance recherchée est de 0,9.
Le nombre de prédicteurs ou de variables explicatives est de 2. Plutôt que de rentrer des paramètres, on sélectionne l'option Taille de l'effet et on prend 0,02 pour un effet faible.

Dans l'onglet Graphique, l'option graphique de simulation est activée et on représentera la taille de l'échantillon 1 sur l'axe vertical et la puissance sur l'axe horizontal.
La puissance varie entre 0,8 et 0,95 par intervalle de 0,01.

Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués, puis les résultats sont affichés.
Interpréter les résultats du calcul de la taille de l'échantillon nécessaire dans le cadre d’une régression linéaire
Le premier tableau rassemble les paramètres utilisés en entrée. Dans notre cas, uniquement le nombre de prédicteurs.

Le second tableau rassemble les résultats du calcul ainsi qu'une interprétation des résultats.

On voit qu'il faut 66 observations par échantillon pour obtenir une puissance la plus proche possible de 0,9.
Le tableau suivant rassemble les calculs obtenus pour chaque valeur de la puissance comprise entre 0,8 et 0,95.

Le graphique de simulation montre l'évolution de la taille de l'échantillon en fonction de la puissance. On voit que pour une puissance de 0,8, il suffit d'un peu plus de 50 observations par échantillon et que pour une puissance de 0,95 on arrive à 80 observations.

Pour des tailles d'effet de 0,15 et 0,35, on obtient les résultats suivants :

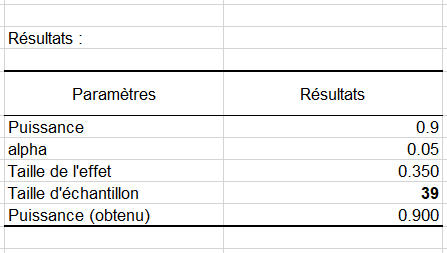
La taille de l'échantillon va donc baisser car le R² va s'éloigner de 0 et on voit que pour une forte différence, 39 observations seront suffisantes.
Ainsi si on suppose que la qualité d'explication de la taille d'un enfant par les variables poids et âge est fort (R² proche de 1), il suffira donc de 39 observations pour obtenir une puissance de 0,9.
XLSTAT est donc un outil puissant aussi bien pour rechercher la taille de l'échantillon requise pour une analyse que pour calculer la puissance d'un test. Évidemment, si l'utilisateur dispose de plus d'informations sur ses échantillons, il pourra donner des détails sur les paramètres en entrée, plutôt que de rentrer la taille de l'effet. Il est aussi possible de tester l'effet de l'ajout de variables explicatives à un modèle.
Cet article vous a t-il été utile ?
- Oui
- Non