Partitionnement univarié dans Excel

Ce tutoriel explique comment mettre en place et réaliser un partitionnement univarié dans Excel avec le logiciel XLSTAT.

Le partitionnement univarié est une méthode statistique qui vise à regrouper N observations unidimensionnelles (décrites par une seule variable quantitative) dans K classes homogènes.

Jeu de données pour effectuer un partitionnement univarié avec XLSTAT

Les données contiennent les notes d’une classe de 29 élèves dans 8 matières : Mathématiques, Chimie, Anglais, Français, Physique, Histoire, Sport et Espagnol. Les notes varient entre 0 et 20. Chaque ligne correspond à un élève et chaque colonne à une matière.

L’objectif de ce partitionnement univarié est de créer cinq groupes de niveau homogènes dans chaque matière.

Paramétrer le calcul d’un partitionnement univarié avec XLSTAT

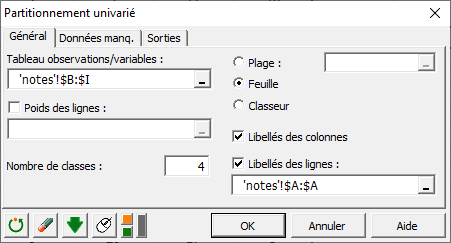Une fois XLSTAT lancé, sélectionnez la fonction Partitionnement univarié dans le menu Analyse des données. La boîte de dialogue Partitionnement univarié apparaît. Dans l’onglet Général, sélectionnez les données sur la feuille Excel. Le champ Tableau observations/variables doit contenir l'ensemble de notes (colonnes B à I).

Ici, les lignes n’ont pas des poids (ou importance) différents car un élève n’est pas plus significatif que les autres pour la constitution des groupes. On ne coche pas et ne spécifie pas de Poids des lignes.

Le Nombre de classes correspond au nombre de groupe à créer dans chaque matière, c’est-à-dire 4. Enfin, nous cochons les Libellés des colonnes (car nous avons précisé le nom des matières) et nous cochons et spécifions les Libellés des lignes (numéros des élèves). Ici, il s’agit de la colonne A. Dans l’onglet Données manquantes, nous choisissons ici de ne pas accepter les données manquantes car les élèves doivent tous avoir une note dans chaque matière. Enfin, dans l’onglet Sorties, nous cochons toutes les sorties pour pouvoir observer et décrire toutes les informations concernant chaque matière.

Une fois que vous avez appuyé sur le bouton OK, les calculs commencent puis les résultats sont affichés.

Interpréter les résultats d’un partitionnement univarié avec XLSTAT

Le partitionnement univarié renvoie plusieurs résultats sous forme de tableaux. Tout d’abord, nous pouvons voir un tableau descriptif récapitulatif.

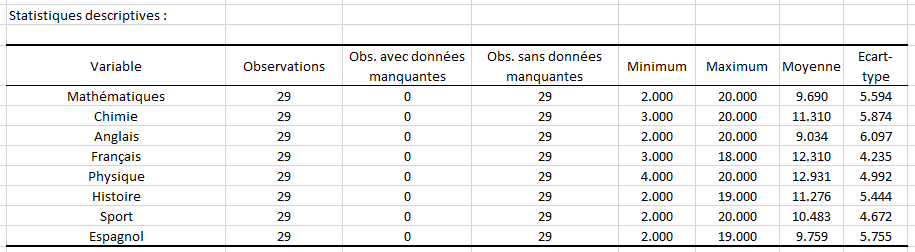Pour chaque variable, nous avons 29 observations, dont 0 données manquantes car tous les élèves ont une note dans chaque matière. Nous pouvons également voir le minimum, maximum, moyenne et écart-type par matière. Par exemple, en mathématiques la moins bonne note est 2, la meilleure note est 20. La moyenne de la classe est de 9.69. L’écart-type est de 5.594, ce qui signifie que la majorité des notes se trouvent entre 4,1 et 15,3 environ.

Comme il s’agit d’un partitionnement univarié, l’analyse est réalisée indépendamment pour chaque matière. Nous allons décrire les résultats concernant les Mathématiques.

En premier lieu, nous voyons les barycentres initiaux des classes. Nous voyons qu’ils sont bien distincts, celui de la classe 1 étant à 2.167, de la classe 2 à 6, de la classe 3 à 10, de la classe 4 à 14.143 et enfin celui de la classe 5 à 18.25.

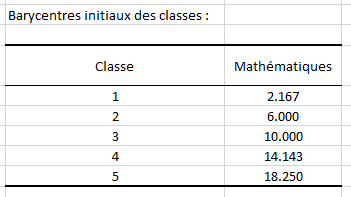Après application du partitionnement, les barycentres n’ont pas changé. Nous voyons également la somme des poids qui représente ici le nombre d’individus dans chaque classe (vu que tous les élèves ont la même importance) et la variance intra-classe. Ici, la classe la plus homogène est la classe 3 car elle a la plus petite variance intra-classe. La classe la moins homogène est donc la classe 5. 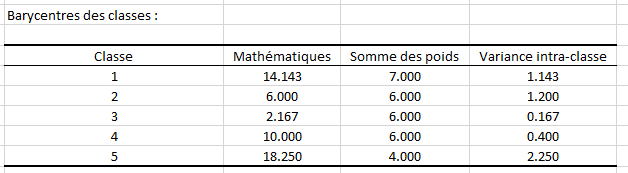Ensuite, nous avons un tableau récapitulant la distance entre les barycentres des classes. Les classes 3 et 5 sont les plus éloignées par environ 16 points. Le barycentre (ou note moyenne) des élèves de la classe 3 est en effet de 2.17/20 alors que celui de la classe 5 est de 18.25/20.

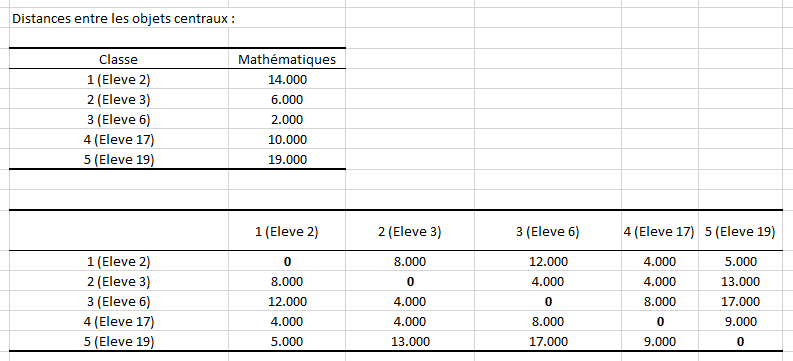
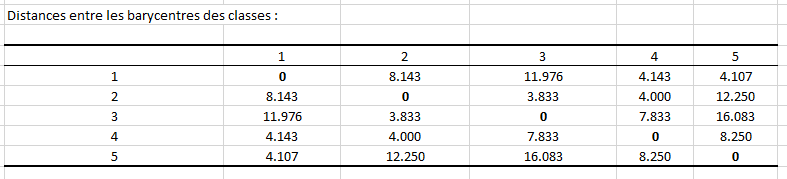Nous pouvons mener un raisonnement similaire concernant les objets (ici élèves) centraux de chaque classe, c’est-à-dire ceux ayant obtenu la note médiane de leur classe. Nous voyons que l’élève 6 (centre de la classe 3) a obtenu 2/20 en mathématiques alors que l’élève 19 (centre de la classe 5) a obtenu 19/20, ce qui montre une fois de plus l’écart entre les classes 3 et 5.

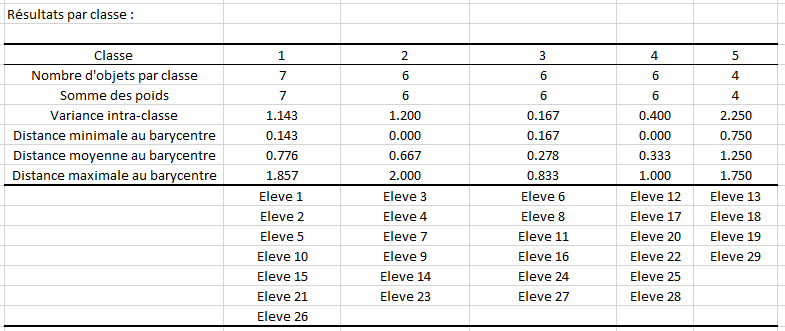
Observons maintenant les résultats détaillés par classe ainsi que la liste des élèves présents dans chacune d’elles. Nous voyons que les groupes de niveau comporteront entre 4 et 7 élèves. Comme vu précédemment, la variance intra-classe nous indique que le groupe 3 est le plus homogène et le groupe 5 le moins homogène. Les distances minimale, maximale et moyenne au barycentre nous donnent des informations sur les résultats des élèves présents dans chaque groupe par rapport à la note moyenne du groupe. Dans le groupe 1, les élèves ont en moyenne 0.77 points en plus ou en moins par rapport à la note moyenne du groupe.

Enfin, nous avons la constitution des groupes : par exemple, le groupe 2 est constitué des élèves 3, 4, 7, 9, 14 et 23. Ceci est cohérent si on regarde les données brutes : en effet, la note moyenne du groupe 2 est de 6. Les élèves 3, 4, 7, 9, 14 et 23 ont eu respectivement 6, 6, 5, 6, 8 et 5 sur 20.

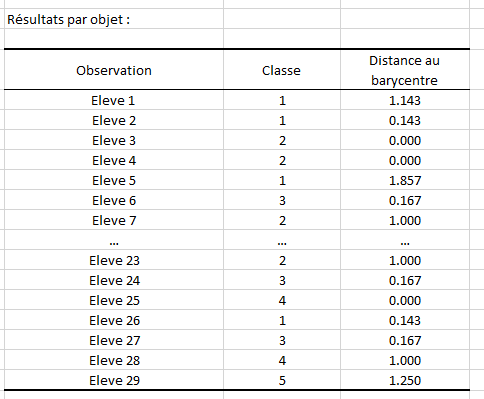
Pour terminer, nous avons un tableau qui récapitule le groupe de niveau (=classe) auquel appartient chaque élève ainsi que son écart par rapport à la note moyenne du groupe (=distance au barycentre).

Conclusion

En conclusion, le partitionnement univarié nous a permis de classer les élèves d’une même classe dans des groupes de niveau indépendamment pour chaque matière. Pour savoir plus sur le choix de la méthode de classification la plus approprié pour vos données, consultez notre article Choisir une méthode de classification avec XLSTAT .