Régression logistique multinomiale dans Excel

Ce tutoriel explique comment calculer et interpréter une Régression logistique multinomiale avec Excel en utilisant XLSTAT.

Modèle logit multinomial

Le modèle logit multinomial consiste en une généralisation du modèle logit classique pour des variables à expliquer ayant plus de deux modalités (cette méthode peut aussi être appelée régression logistique polytomique).

Le principe de ce modèle est le suivant : on veut comprendre ou prédire l'effet d'une ou plusieurs variables sur une variable qualitative à réponses multiples. Cette variable doit être une variable catégorielle non ordonnée. L’ensemble des calculs se font relativement à une modalité de référence que l’utilisateur devra sélectionner. On pourra ainsi comprendre l’impact du choix d’une modalité en fonction des variables explicatives relativement à une modalité fixée.

Le modèle logit multinomial permet de modéliser la probabilité qu'un événement survienne étant donné les valeurs d'un ensemble de variables descriptives quantitatives et/ou qualitatives.

Jeu de données pour la création d'un modèle logit multinomial

Le jeu de données que nous utilisons est issu du livre « multivariate interpretation of clinical laboratory data » de Adelin Albert et Eugene K. Harris. Ce jeu de données comporte 218 observations issues de patients atteints de maladies du foie (Plomteux, 1980).

Les patients ont été répartis en quatre groupes correspondants à quatre maladies du foie : - l'hépatite virale aiguë (groupe 1 : 57 patients) ;

• l'hépatite chronique persistante (groupe 2 : 44 patients) ;
• l'hépatite chronique agressive (groupe 3 : 40 patients) ;
• la cirrhose post-nécrotique (groupe 4 : 77 patients).

Le diagnostic a été établi à partir de quatre enzymes hépatiques (U/L) : - l’aspartate aminotransférase (X1 : abrégé AST) ;

• l’alanine aminotransférase (X2 : ALT) ;
• la glutamate déshydrogénase (X3 : GLDH) ;
• et l’ornithine carbonyltransférase (X4 : OCT).

Le diagnostic d'hépatite virale aiguë était basé sur les signes clinico-biologiques classiques tandis que tous les autres patients ont été diagnostiqués suite aux résultats de la laparoscopie et de la biopsie.

Objectif de ce modèle logit multinomial

Dans l'exemple que nous traitons, nous cherchons à prédire la probabilité pour qu'un patient soit atteint d’une des maladies mentionnées ci-dessus. La variable à expliquer comprend quatre modalités correspondant aux quatre maladies du foie.

Paramétrer un modèle logit multinomial

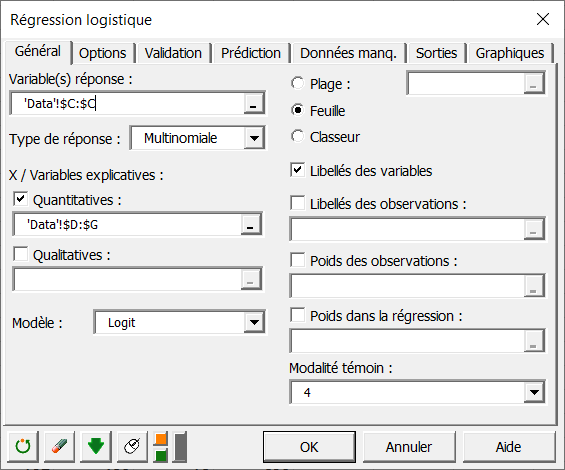
Pour activer la boîte de dialogue du modèle logit multinomial, lancez XLSTAT, puis choisissez XLSTAT / Modélisation des données / Régression logistique. Une fois que vous avez cliqué sur le bouton, la boîte de dialogue apparaît. Sélectionnez ensuite l’option multinomiale comme type de réponse.

Sélectionnez les données sur la feuille Excel. Les données Réponse correspondent à la colonne dans laquelle se trouve la variable à expliquer, à savoir ici la colonne Groupe.

Dans notre cas il y a quatre variables explicatives quantitatives correspondant aux quatre enzymes AST, ALT, GLDH, OCT.

Comme nous avons sélectionné les libellés des variables, nous devons sélectionner l'option Libellés des variables.

On peut sélectionner comme modalité témoin, la modalité 4. Cela n’influence aucunement les calculs et les prédictions, mais seulement la façon dont les équations du modèle sont écrites. De nombreuses autres options sont disponibles dans les autres onglets de la boîte de dialogue (pour de plus amples détails, voir l’aide de XLSTAT).

Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués puis les résultats affichés.

Interpréter les résultats d'un modèle logit multinomial

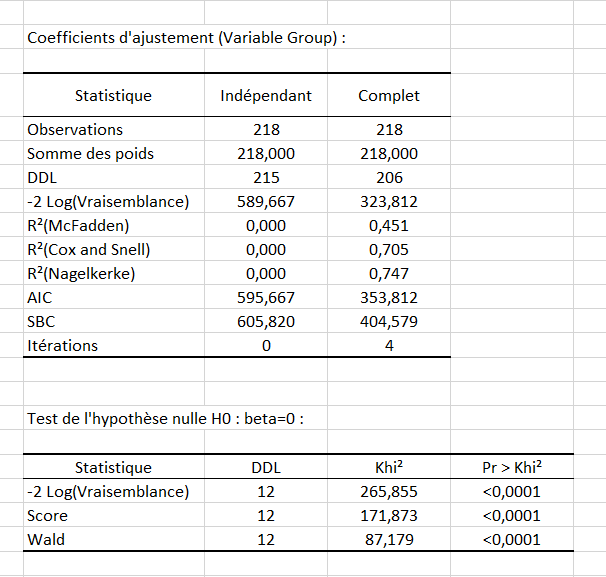
Le tableau des coefficients d’ajustement donne plusieurs indicateurs de la qualité du modèle (ou qualité de l'ajustement). Ces résultats sont équivalents au R² de la régression linéaire et au tableau d'analyse de la variance ANOVA. La valeur la plus importante est le Khi² associé au Log ratio (L.R.). C'est l'équivalent du test F de Fisher du modèle linéaire : on essaie d'évaluer si les variables apportent une quantité d'information significative pour expliquer la variabilité de la variable réponse. Dans notre cas, comme la probabilité est inférieure à 0.0001, on peut conclure que les variables apportent une quantité significative d'information. Ensuite le tableau de l’analyse de Type II donne les premiers détails sur le modèle. Il est utile pour évaluer la contribution des variables à l’explication de la variable réponse. 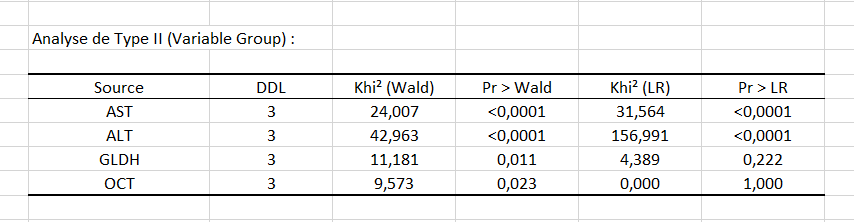D’après la probabilité associée aux tests du Khi², nous pouvons voir que les variables qui influencent le plus le choix du groupe sont les enzymes hépatiques AST et ALT.

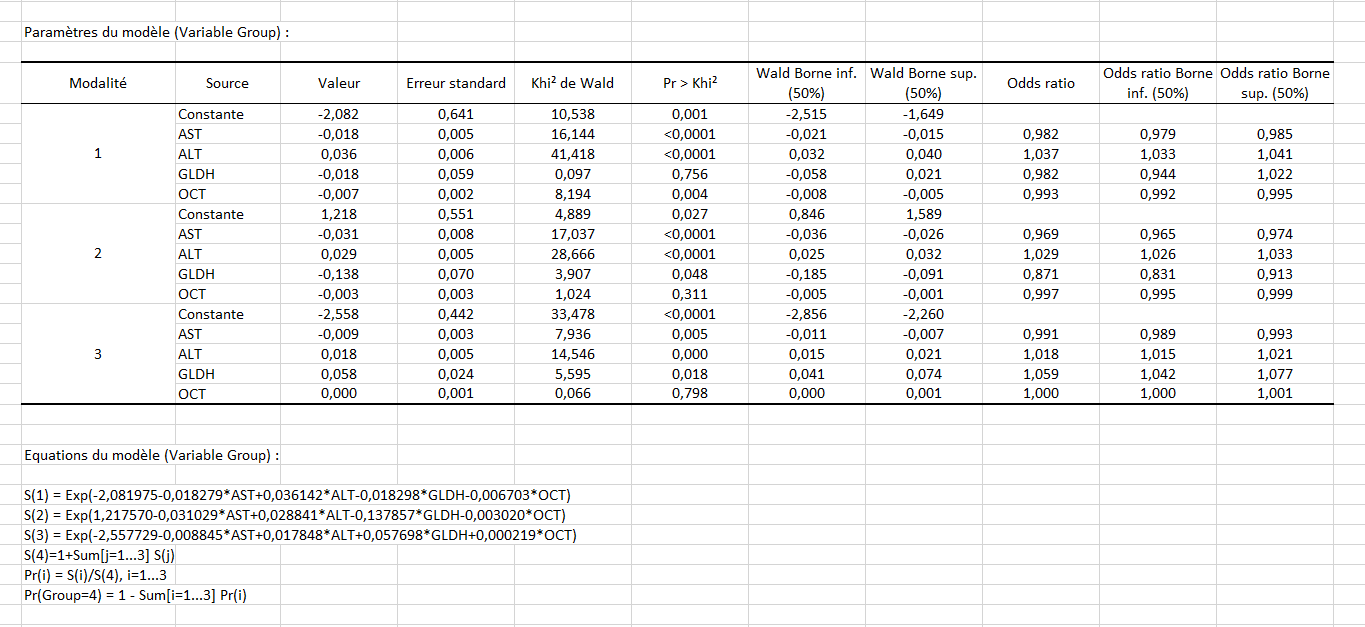
Le tableau des paramètres du modèle permet ensuite de tester non plus chaque variable globalement, mais son influence sur chacune des modalités par rapport à celle de référence (ici 4). Ainsi, nous voyons que par rapport à la modalité de référence, les modalités 2 et 3 sont influencées par la variable GLDH, puisque le coefficient est significatif (respectivement 0.048 et 0.018), ce qui n’est pas le cas de la modalité 1 (0.756). De plus, avoir une valeur élevée de GLDH influe sur le fait d’avoir plus de chance d’avoir la maladie 3 par rapport à la 4 (car le coefficient est positif, 0.058, et la pvalue significative, 0.018).

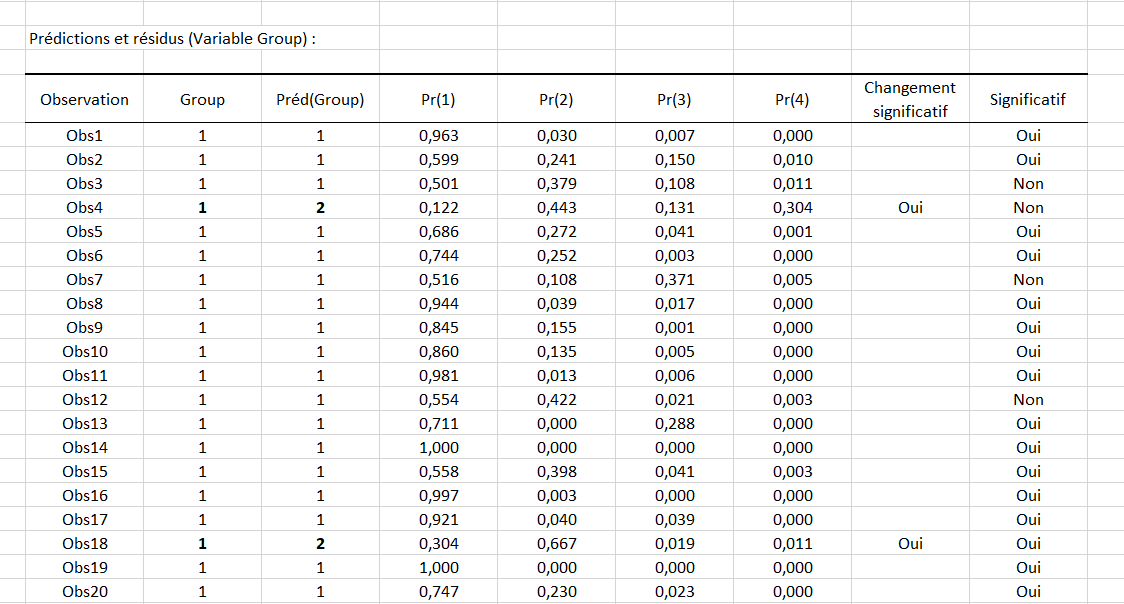
Par la suite, vous pouvez visualiser le tableau des Prédictions et résidus. Nous voyons que la quatrième observation est associée au groupe 1, mais le modèle prédit qu’elle devrait appartenir au groupe 2. En effet nous pouvons voir que la probabilité d’être dans le groupe 2 est la plus importante et est estimée à 0.443 tandis que la probabilité d’être dans le groupe 1, 3 et 4 est estimée à respectivement 0.122, 0.131 et 0.304.

La colonne Changement significatif nous indique que le changement de valeur entre la modalité prédite et celle du jeu de données est significatif. La deuxième colonne Significatif indique quant à elle, quelle que soit la modalité retenue, si la probabilité pour cette modalité est significativement supérieure ou non à celles des autres modalités.

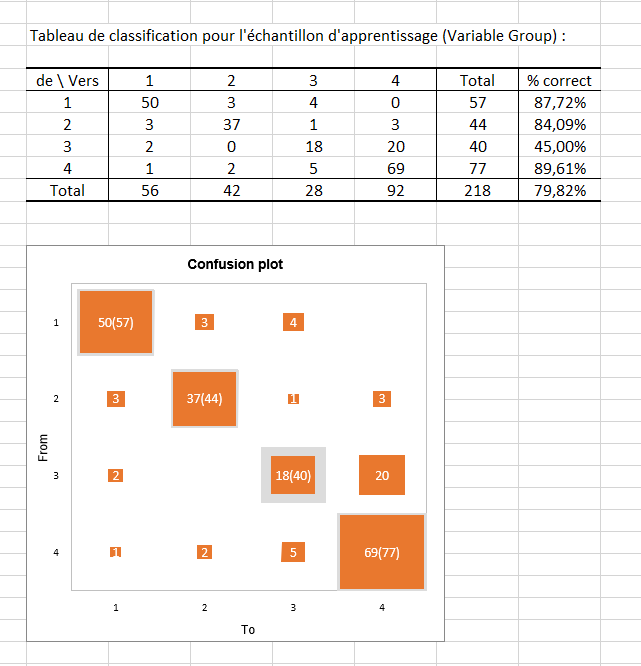
Dans le cas de la dix-huitième observation, nous pouvons voir que le changement est significatif et la probabilité retenue pour le groupe 2 (0.667) est supérieure à celle des autres modalités (0.304, 0.019 et 0.011). A noter que ces deux colonnes apparaissent si l’option Analyse de significativité a été cochée dans l’onglet « Sorties » de la boite de dialogue. Le tableau de classification pour l'échantillon d'apprentissage (parfois appelée matrice de confusion) est ensuite affiché dans le rapport. Ce tableau permet de visualiser le pourcentage d'observations bien classées pour chaque modalité (vrais positifs et vrais négatifs). Par exemple, nous pouvons voir que les observations des modalités 1, 2 et 4 ont respectivement bien été classées à 87.72%, 84.09% et 89.61% alors que les observations de la modalité 3 n’ont été bien classées que dans 45% des cas.

Le confusion plot permet de visualiser synthétiquement ce tableau. Les carrés en gris sur la diagonale représentent les effectifs observés pour chaque modalité. Les carrés orange représentent quant à eux, les effectifs prédits pour chaque modalité. Ainsi, nous pouvons voir que les surfaces des carrés se superposent quasiment intégralement pour la modalité 1 (50 observations prédites sur 57 observations observées), la modalité 2 (37 observations prédites sur 44 observations observées) et la modalité 4 (69 observations prédites sur 77 observations observées) contrairement à la modalité 3 (18 observations prédites sur 40 observations observées). 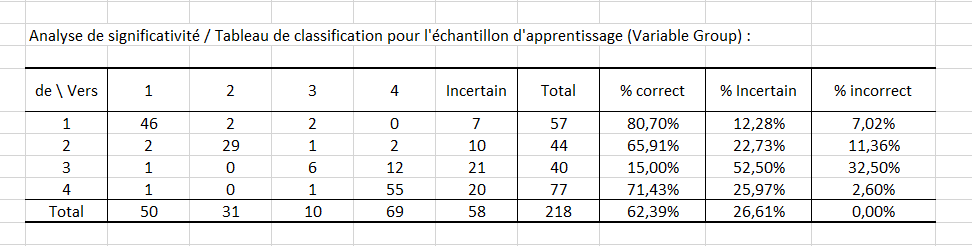Enfin, les deux derniers tableaux prennent en compte l’incertitude. Par exemple, le premier tableau montre que pour 12 observations, la valeur de départ est la modalité 3, la valeur de prédiction est la modalité 4 et la significativité est à « Oui » (voir le tableau prédictions et résidus pour retrouver ces effectifs). Autrement dit, il y a 12 observations pour lesquelles la modalité prédite est significative.

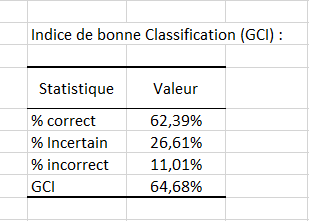
Environ la moitié (52.50%) des valeurs prédites par le modèle pour la modalité 3 peuvent être considérées comme incertaines, alors que dans le cas de la modalité 1 les valeurs prédites par le modèle sont les moins incertaines puisque le pourcentage d’incertitude est estimé à 12.28%. Enfin, le dernier tableau nous indique que 62.39% des observations ont été bien classées (vrais positifs), 26.61% ont un classement incertain et 11.01% ont été mal classées (faux positifs et faux négatifs cumulés). L’indice GCI (Goodness of Classification Index), quant à lui, est de 64.68%, ce qui signifie que la qualité prédictive de ce modèle de classification est satisfaisante.