Analyse Factorielle Multiple AFM dans Excel
Ce tutoriel explique comment mettre en place l'Analyse Factorielle Multiple (AFM) sur des tableaux de fréquences dans Excel avec le logiciel XLSTAT.
L’Analyse Factorielle Multiple (AFM), permet d’analyser simultanément plusieurs tableaux de variables, et d’obtenir des résultats, notamment des représentations graphiques, qui permettent d’étudier la relation entre les observations, les variables et les tableaux.
A l’intérieur d’un tableau les variables doivent être de même nature (quantitative ou qualitative), mais les tableaux peuvent être de différents types.
Cette méthode a été développée par Escofier et Pagès dès 1984. Un livre de ces mêmes auteurs permet d'en découvrir à la fois les aspects pratiques et théoriques : Analyse factorielles simples et multiples : Objectifs, méthodes et interprétation.
La méthodologie de l'Analyse Factorielle Multiple se décompose en deux étapes :
- On réalise successivement pour chacun des tableaux une ACP ou une ACM en fonction de la nature des variables. On conserve la valeur de la première valeur propre de chacune des analyses pour pondérer ensuite les différents tableaux dans la seconde partie de l’analyse.
- On réalise ensuite une ACP pondérée sur les colonnes de l’ensemble des tableaux, sachant que les tableaux de variables qualitatives sont transformés en tableaux disjonctifs complets, chacune des indicatrices ayant un poids fonction de la fréquence de la modalité concernée. La pondération des tableaux permet d’éviter que les tableaux comprenant plus de variables ne pèsent trop dans l’analyse.
Jeu de données pour réaliser une Analyse Factorielle Multiple
Les données utilisées dans ce tutoriel ont été recueillies par Asselin C. et Morlat R. de l'INRA, d'Angers dans le cadre d'une étude dont les résultats sont présentées dans [ASSELIN C., PAGES J., and MORLAT R. (1992). Typologie sensorielle du Cabernet Franc et influence du terroir. Utilisation de méthodes statistiques multidimensionnelles. J. Int. Sci. Vigne Vin, 26, 3, 129-154].
Les données correspondent à des dégustations de 21 vins de Loire réalisées par 36 experts. Le tableau des données est composé de 21 observations décrites par 31 dimensions. Les 31 dimensions ont été regroupées en 6 catégories :
- Les 2 premières variables, qualitatives, sont liées à l'origine du vin (appellation et sol);
- les 5 variables suivantes, quantitatives, correspondent aux notes d'olfaction après repos ;
- les 3 variables suivantes, quantitatives, correspondent à des critères visuels ;
- les 10 variables suivantes, quantitatives, correspondent aux notes d'olfaction après agitation ;
- les 9 variables suivantes, quantitatives, correspondent à la gustation ;
- les 2 variables suivantes, quantitatives, correspondent à des notes d'ensemble.
Le but principal de l'étude est de comprendre comment se positionnent les vins les uns par rapport aux autres, et quelles sont les relations entre les différents critères et groupes de critères.
Nous décidons de ne pas utiliser les deux variables qualitatives et les deux dernières variables quantitatives dans la première partie de l'étude, mais de les utiliser seulement en tant que variables supplémentaires, afin de ne garder que les variables sensorielles objectives pour construire les axes.
Paramétrer une Analyse Factorielle Multiple
Pour afficher la boîte de dialogue de l'Analyse Factorielle Multiple, lancez XLSTAT, puis choisissez les commandes XLSTAT-MX / Analyse de données sensorielles / Analyse Factorielle Multiple.
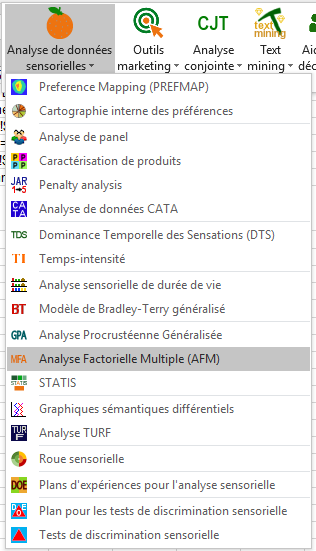
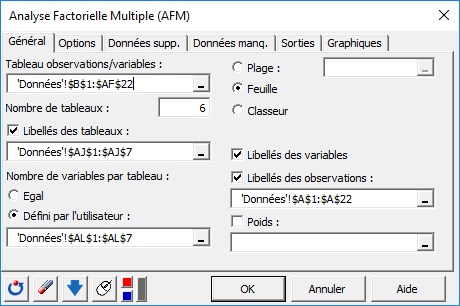
Une fois que vous avez cliqué sur le bouton, la boîte de dialogue apparaît. Sélectionnez alors les données correspondant à l'ensemble des variables à analyser.
Comme nous l'avons vu en haut, les variables sont regroupées en 6 tableaux distincts. On doit alors indiquer à XLSTAT que le nombre de tableaux est 6.
Nous sélectionnons ensuite les noms que nous avons donnés aux 6 tables (terr, olf.rep, vis, olf.agi, gust, global). Nous devons ensuite définir le nombre de variables contenu dans chaque tableau.
Comme le nombre de variables n'est pas le même pour tous les tableaux, nous devons sélectionner la feuille d'Excel la plage de cellules contenant le nombre de variables correspondant à chacun des tableaux.
Comme les en-têtes des colonnes ont été sélectionnées avec les données, nous activons l'option Libellés des variables.
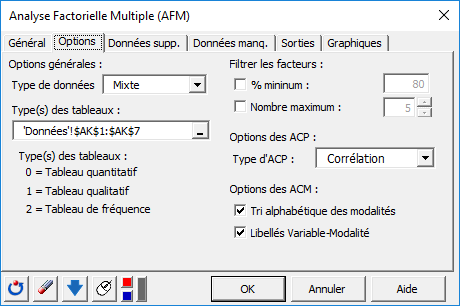
Cliquez alors sur l'onglet Options pour saisir des informations complémentaires.
Nous avons ici deux types de tableaux : des tableaux de données quantitatives et des tableaux de données qualitatives. Pour cette raison nous choisissons le type de données Mixte, puis nous sélectionnons la colonne où les types sont indiqués (0 pour quantitatif, 1 pour qualitatif).
Nous activons également l'option Graphiques sur deux axes pour éviter d'être sollicités pour définir les axes pour les analyses pour les différentes cartes factorielles.
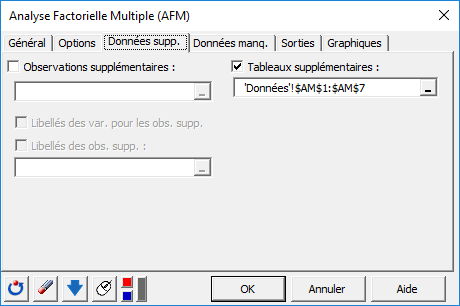
Enfin, nous activons l'onglet Données supplémentaires tab, afin de préciser quels tableaux doivent être pris en compte pour les calculs, et ceux qui seront considérés comme supplémentaires.
Pour cela, nous sélectionnons la colonne indiquant si les tableaux sont actifs (1) ou supplémentaires (0). Les tableaux supplémentaires sont aussi appelés tableaux illustratifs.
Après que vous ayez cliqué sur le bouton OK, les calculs commencent et les résultats sont affichés sur une nouvelle feuille Excel.
Interpréter les résultats d'une Analyse Factorielle Multiple
Le premier ensemble de résultats correspond aux statistiques descriptives des diverses variables. Les résultats concernant les variables des tableaux supplémentaires sont affichés en bleu.
Ensuite, des analyses séparées sont effectuées pour chacun des tableaux. Si le tableau comprend des variables quantitatives, une Analyse en Composantes Principales (ACP) est réalisée. Si le tableau comprend des variables qualitatives, une Analyse des Correspondances Multiples (ACM) est réalisée. Ainsi, dans notre cas, une ACM est réalisée, suivie de 5 ACP. Les résultats de ces analyses préliminaires sont ensuite utilisés dans l'analyse finale, la seconde partie de l'AFM, qui est en fait une ACP pondérée (les poids affectant ici les colonnes). Les résultats de l'AFM commencent par l'analyse des valeurs propres de l'ACP pondérée. Nous pouvons voir ici qu'avec les deux premiers facteurs nous avons presque 70% de la variabilité.

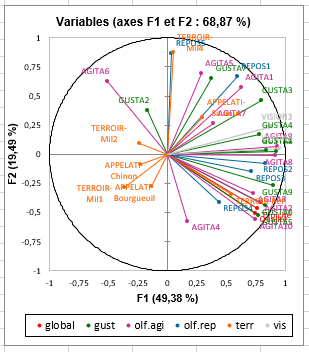
Ensuite, nous analysons le cercle des corrélations des variables. Ce graphique permet de constater que les variables de jugement général (typicité et qualité) sont fortement liées à quelques variables (AGITA3 et GUSTA5, par exemple), et elles sont corrélées avec le premier axe. Nous pouvons également confirmer le fait que les variables de vision sont fortement corrélées avec le premier axe. Nous voyons également que les différentes variables « olfaction après agitation » sont réparties dans trois des quatre quadrants du cercle. Enfin, le deuxième facteur est fortement corrélé avec la variable REPOS5.
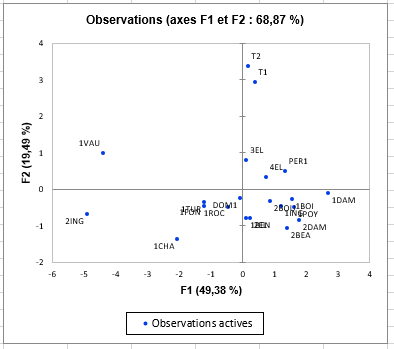
Le graphique suivant montre les observations avec les barycentres (centres de gravité) correspondant aux différentes modalités (ou catégories) des deux variables qualitatives. Nous pouvons voir que les vins T1 et T2 sont très proches l'un de l'autre, et isolés des autres vins. Ils sont fortement liés au deuxième facteur, qui, comme nous l'avons vu plus tôt, est fortement lié à REPOS5. Le vin 1DAM a la coordonnée la plus élevée sur le premier axe. Nous pouvons également voir que le vin 2DAM est dans la direction des deux variables de jugement global (typicité et qualité). Ce sont sans aucun doute les deux vins préférés. Nous pouvons voir que le sol de référence Ref est aussi dans cette direction. A l'opposé, le vin 1VAU est celui qui a le moins plu aux juges.
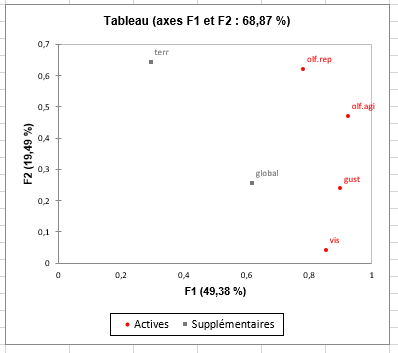
Les coordonnées des tableaux sont alors affichées et utilisées pour créer le graphique de représentation des tableaux. Nous pouvons voir sur le graphique que le premier axe est fortement lié aux quatre tableaux actifs (les coordonnées et les contributions sont élevées). Le deuxième facteur est la surtout lié à l'olfaction après repos, et à un moindre degré, à l'olfaction après agitation.
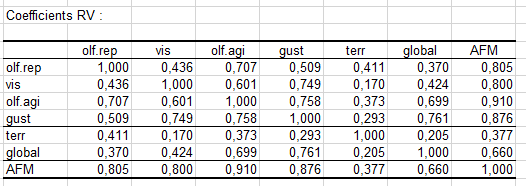
Les coefficients Lg de liaison entre les tableaux permettent de mesurer à quel point les tableaux sont liés deux à deux. Les coefficients RV (voir ci-dessous) de liaison entre les tableaux sont une autre mesure dérivée des coefficients Lg. La valeur des coefficients de RV est comprise entre 0 et 1, ce qui en facilite l'interprétation. Nous pouvons voir ici que les deux tableaux les plus liés sont la gustation et l'olfaction après agitation. Plus surprenant, nous voyons que le coefficient de RV de la gustation et de la la vision est élevé.
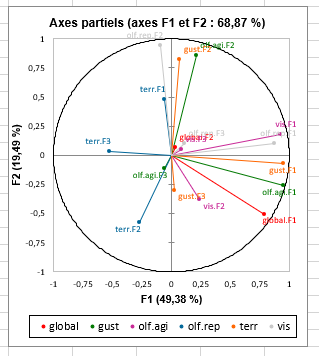
Le graphique des axes partiels permet de voir quels facteurs des analyses séparées de la phase 1 de l'AFM sont corrélés avec les axes de la phase 2 de l'AFM. On peut voir qu'ici les facteurs des analyses séparés sont fortement corrélés avec les facteurs de l'AFM. Cela n'est cependant pas toujours le cas.
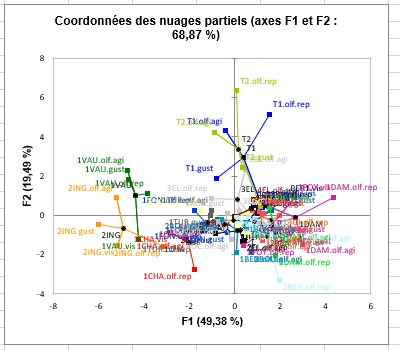
Le dernier graphique est basé sur le précédent, mais aux observations sont ajoutés les nuages partiels, et des lignes sont tracées entre l'observation et les points projetés correspondants. Les nuages partiels correspondent aux observations supplémentaires pour lesquelles seulement l'information fournie par un tableau est prise en compte, les valeurs pour les autres tableaux étant mises à 0. Cela permet de visualiser comment les différents tableaux influencent la position d'un point donné. Par exemple, pour vin T2, nous voyons que l'olfaction après repos tend à rendre le vin encore plus différent des autres vins. Pour d'autres vins, par exemple 2BEA et 1DAM, nous observons le même phénomène.
En conclusion, l'AFM est une méthode intéressante et riche parce qu'elle permet d'analyser des jeux de données complexes, tout en fournissant de nombreux résultats graphiques : nous pouvons visualiser les tableaux (dans lesquels les variables sont regroupées), les variables elles-mêmes, et les observations. Dans cet exemple particulier, l'AFM nous a permis de représenter les vins en deux dimensions, et d'interpréter rapidement leur position.
Cet article vous a t-il été utile ?
- Oui
- Non