Analyse Factorielle Multiple sur des tableaux de fréquences dans Excel

Ce tutoriel explique comment mettre en place l'Analyse Factorielle Multiple (AFM) sur des tableaux de fréquences dans Excel avec le logiciel XLSTAT.

L’Analyse Factorielle Multiple (AFM), permet d’analyser simultanément plusieurs tableaux de variables, et d’obtenir des résultats, notamment des représentations graphiques, qui permettent d’étudier la relation entre les observations, les variables et les tableaux.

La méthodologie de l'Analyse Factorielle Multiple sur tableaux de fréquences se décompose en deux étapes :

• On réalise successivement pour chacun des tableaux une Analyse Factorielle des correspondances (AFC). On conserve la valeur de la première valeur propre de chacune des analyses pour pondérer ensuite les différents tableaux dans la seconde partie de l’analyse.
• On réalise ensuite une Analyse en Composantes Principales ACP pondérée sur les colonnes de l’ensemble des tableaux. La pondération des tableaux permet d’éviter que les tableaux comprenant plus de variables ne pèsent trop dans l’analyse.

Nous étudierons ici le cas particulier de l’AFM sur des tableaux de fréquences. Pour une description plus générale de l’AFM et son utilisation sur d’autres types de tableaux vous pouvez vous reporter au tutoriel en lien ici.

Jeu de données pour lancer une Analyse Factorielle Multiple sur des tableaux de fréquences

Les données utilisées dans ce tutoriel sont un extrait des données collectées par LAURIE E. FRIDAY., et utilisée dans l’article suivant : [Friday, L.E. (1987) The diversity of macroinvertebrate and macrophyte communities in ponds, Freshwater Biology, 18, 87–104.]. Ces données correspondent à un comptage d’espèces classées selon leur groupe d’appartenance sur différents sites. On dispose au total de 62 espèces réparties en 5 groupes et les mesures de comptage ont été effectuées sur 12 sites différents, les espèces sont réparties de la manière suivante :

• Le tableau 1 contient 6 espèces appartenant au groupe Oligochaeta.
• Le tableau 2 contient 13 espèces appartenant au groupe Coleoptera.
• Le tableau 3 contient 13 espèces appartenant au groupe Trichoptera.
• Le tableau 4 contient 8 espèces appartenant au groupe Mollusca.
• Le tableau 5 contient 22 espèces appartenant au groupe Diptera.

L’objectif principal de l'étude est de comprendre comment se positionnent les sites les uns par rapport aux autres, et quelles sont les relations entre les différents groupes d’espèces.

Paramétrer une Analyse Factorielle Multiple sur des tableaux de fréquences

Pour afficher la boîte de dialogue de l'Analyse Factorielle Multiple, lancez XLSTAT, puis choisissez les commandes Fonctions avancées / Analyse de données multiblocs / Analyse Factorielle Multiple (AFM). La fonction est également disponible dans le menu Analyse de données sensorielles. Une fois que vous avez cliqué sur le bouton, la boîte de dialogue AFM apparaît.

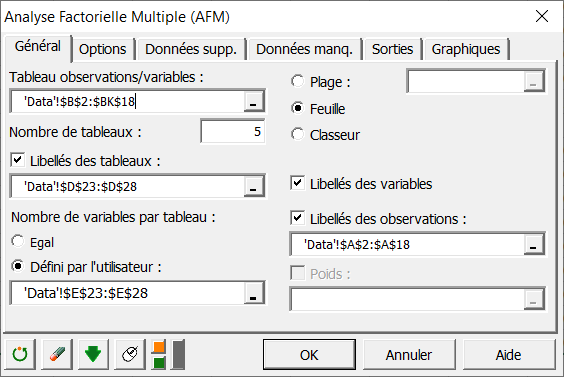
Sélectionnez alors les données correspondant à l'ensemble des variables à analyser. Comme nous l'avons vu en haut, les variables sont regroupées en 5 tableaux distincts. On doit alors indiquer à XLSTAT que le nombre de tableaux est 5.

Nous sélectionnons ensuite les noms que nous avons donnés aux 5 tableaux (Oligochaeta, Coleoptera, Trichoptera, Mollusca et Diptera). On définit ensuite le nombre de variables contenu dans chaque tableau.

Comme le nombre de variables n'est pas le même pour tous les tableaux, nous devons sélectionner la plage de cellules contenant le nombre de variables correspondant à chacun des tableaux.

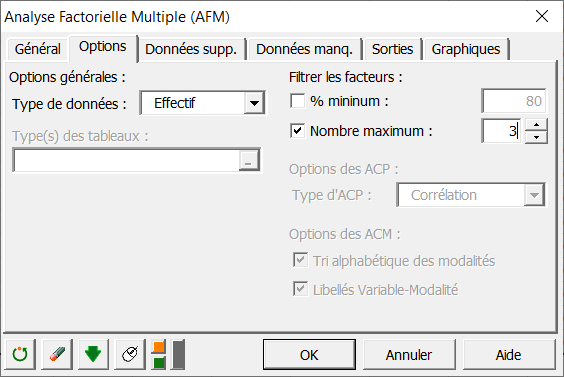
Comme les en-têtes des colonnes ont été sélectionnées avec les données, nous activons l'option Libellés des variables. Cliquez alors sur l'onglet Options pour saisir des informations complémentaires. Nous avons ici des tableaux de fréquences qui correspondent à des effectifs d’espèces sur différents sites, nous sélectionnons donc le type de données Effectif. Nous cliquons ensuite sur le bouton OK, les calculs commencent et les résultats sont affichés sur une nouvelle feuille Excel.

Interpréter les résultats d'une Analyse Factorielle Multiple sur des tableaux de fréquences

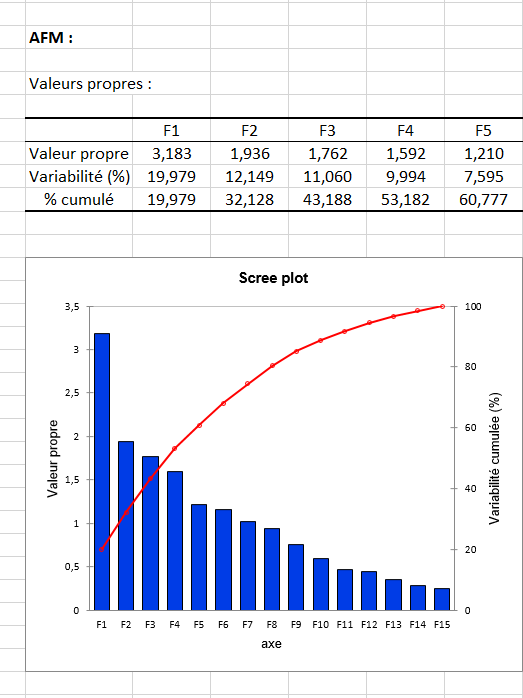
Le premier ensemble de résultats correspond aux statistiques descriptives des diverses variables. Ensuite, des analyses séparées sont effectuées pour chacun des tableaux. Les tableaux sélectionnés étant tous de type « tableau de fréquences » une analyse factorielle des correspondances (AFC) est effectuée sur chacun d’eux. Les résultats de ces analyses préliminaires sont ensuite utilisés dans l'analyse finale, la seconde partie de l'AFM, qui est en fait une ACP pondérée. Les résultats de l'AFM commencent par l'analyse des valeurs propres de l'ACP pondérée. Les premiers résultats concernent les variables (colorées en fonction de leur groupe) et les observations comme dans une ACP classique. 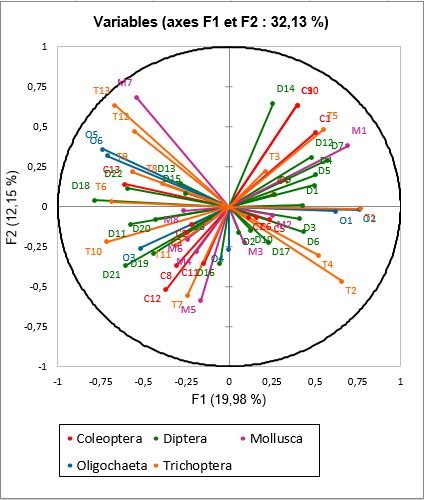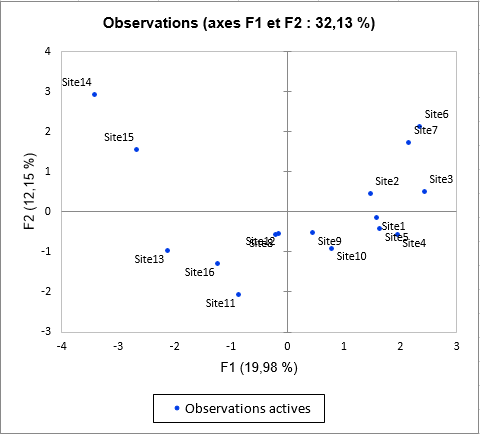En observant le graphique des observations (sites) ci-dessus on remarque un groupe d’observations sur la droite ayant des valeurs positives sur l’axe 1. 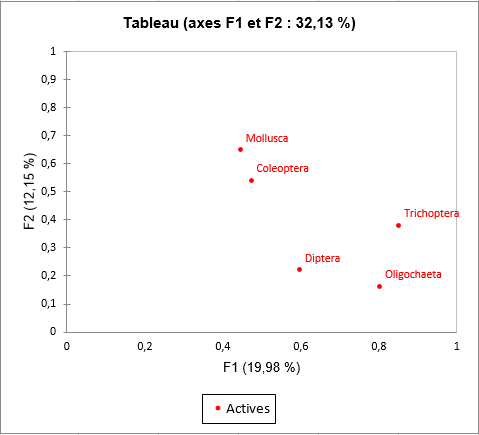Les résultats spécifiques à l’AFM sont ensuite affichés. Tout d’abord, les coordonnées des tableaux sont affichées et utilisées pour créer le graphique de représentation des tableaux. Nous pouvons voir sur le graphique que le premier axe est fortement lié aux tableaux des espèces Trichoptera et Oligochaerta alors que l’axe 2 est lié aux tableaux Mollusca et Coleoptera. 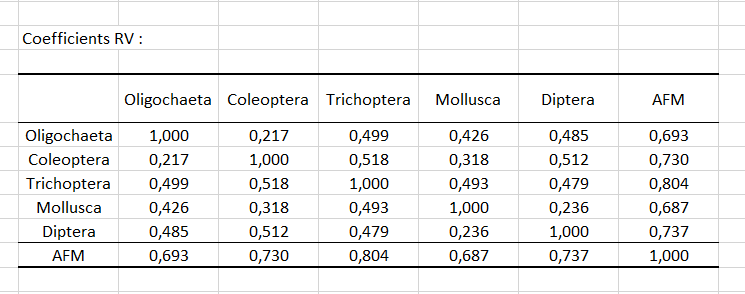Les coefficients Lg de liaison entre les tableaux permettent de mesurer à quel point les tableaux sont liés deux à deux. Les coefficients RV (voir ci-dessous) de liaison entre les tableaux sont une autre mesure dérivée des coefficients Lg. La valeur des coefficients de RV est comprise entre 0 et 1, ce qui en facilite l'interprétation. Nous pouvons voir ici que les deux tableaux les plus liés sont les tableaux Diptera et Coleoptera. Le résultat suivant spécifique à l’AFM correspond à l’analyse des axes partiels. Le graphique des axes partiels permet de voir quels facteurs de chaque analyse séparée de chacun des tableaux sont corrélés avec les axes produits par l'AFM. On voit par exemple que l’axe 1 de l’AFC du tableau Oligochaeta et l’axe 1 de l’AFC du tableau Trichoptera sont fortement corrélés négativement avec l’axe 1 de l’AFM. 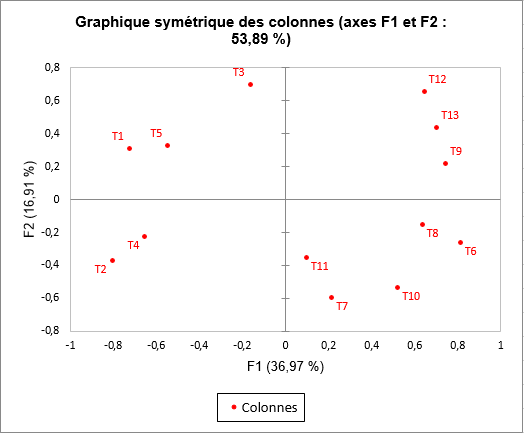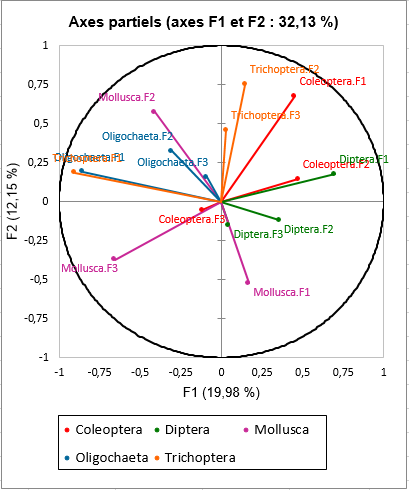Si l’on regarde plus précisément les résultats et notamment les coordonnées des variables de l’AFC du tableau Trichoptera (ligne 517 de la feuille de résultats), on s’aperçoit que des valeurs négatives sur le premier axe de cette AFC correspondent à des fréquences importantes des espèces T1, T2, T3, T4 et T5. 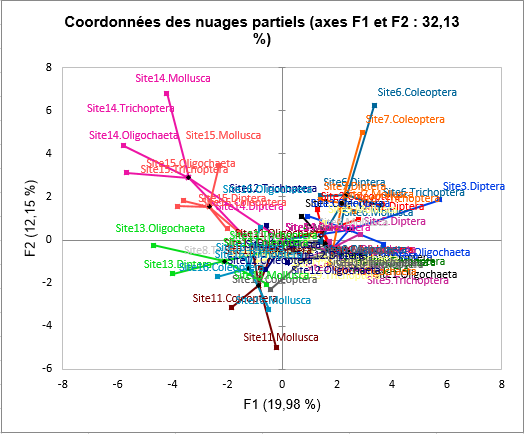Le dernier graphique spécifique à l’AFM est le graphique des nuages partiels. Ce dernier représente les observations pour lesquelles on ajoute les observations partielles, c’est-à-dire les observations vues selon les différents tableaux. Les nuages partiels correspondent aux observations pour lesquelles seulement l'information fournie par un tableau est prise en compte, les valeurs pour les autres tableaux étant mises à 0. Ces observations sont ensuite projetées sur les axes comme des observations supplémentaires. Cela permet de visualiser comment les différents tableaux influencent la position d'un point donné. Par exemple, pour le site 14 on voit que le tableau Mollusca tend à rendre ce site encore plus différent des autres, ceci est aussi vrai pour le site 11 et le tableau Mollusca en bas du graphique.

Conclusion

En conclusion, l'AFM sur des tableaux de fréquences est une méthode intéressante et riche car elle permet d'analyser des jeux de données complexes, tout en fournissant de nombreux résultats graphiques : nous pouvons visualiser les tableaux (dans lesquels les variables sont regroupées), les variables elles-mêmes, et les observations. Dans cet exemple, l'AFM nous a permis de représenter les sites en deux dimensions, et d'interpréter rapidement leur position.