Histogrammes et ajustement de loi de probabilité avec Excel

Le but de ce tutoriel est de créer des histogrammes pour une variable discrète et ensuite tester si un échantillon des 200 valeurs suit une loi binomiale négative sous Excel avec XLSTAT.

Jeu de données pour créer des histogrammes et faire un test d'ajustement à une loi de probabilité

Les données correspondent à une expérience où 200 échantillons d'eau prélevés dans une rivière ont été mis en culture sur un milieu nutritif, afin de déterminer la présence ou non de bactéries de type Escherichia coli. Le nombre de colonnies a été compté après trois jours d'incubation. Dans la colonne "Bact-Data" se trouve le résultat des comptages pour chacun des 200 échantillons.

La loi binomiale négative représente souvent bien le phénomène d'agrégation/dispersion des bactéries dans les milieux aquatiques.

Créer un histogramme

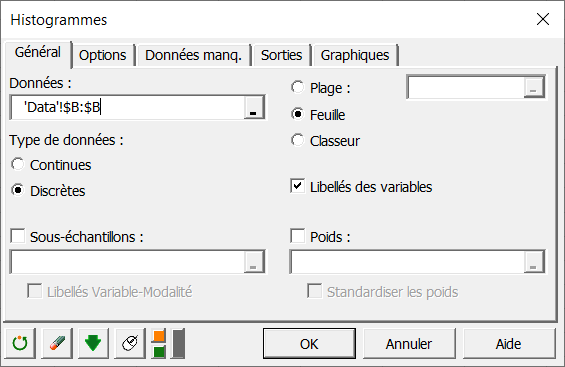
Une fois XLSTAT lancé, choisissez la commande XLSTAT / Visualisation des données / Histogrammes. Une fois le bouton cliqué, la boîte de dialogue apparaît. Vous pouvez alors sélectionner les données sur la feuille Données. L'option Discrètes est activée car les données de comptage sont bien des données discrètes. L'option Libellé des échantillons est laissée activée car la première ligne de la colonne de données comprend le nom de la variable.

Interprétation des résultats de l'histogramme

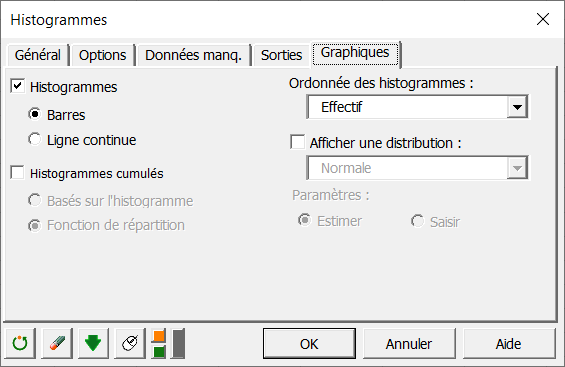
Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués, puis l'histogramme est affiché, suivi du tableau servant à la construction de l'histogramme (voir feuille "Histogramme"). 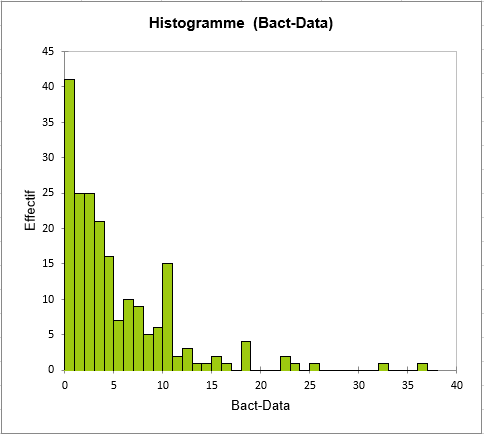Nous voyons que la classe la plus nombreuse est la classe 0, et qu'elle représente plus de 20% des données. Autrement dit dans plus d'un échantillon d'eau sur cinq, aucune bactérie n'a pu être mise en évidence. Ensuite, on observe une décroissance rapide et assez régulière des fréquences relatives. Dans un échantillon, on a trouvé jusqu'à 36 colonies. La vidéo suivante montre comment régler les paramètres pour générer le même histogramme.

Créer un histogramme avec des intervalles spécifiés

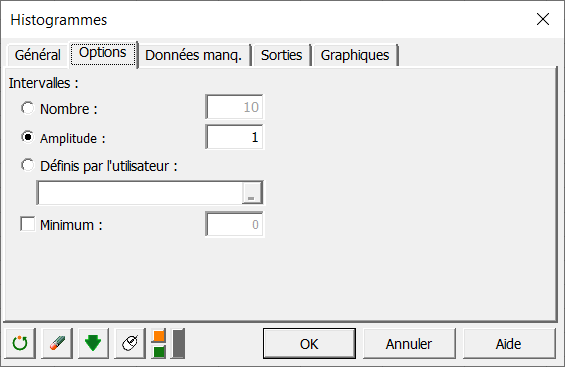
Comme nous voulons faire ensuite un test d'ajustement à la loi binomiale négative (le test du Khi’² nécessite qu'il y ait au moins 5 données par classe), et étant donnée l'imprécision des comptages de bactéries, il semble nécessaire de regrouper les comptages dans des classes plus importantes. Pour cela on crée une liste de bornes (0,1,2,3,4,5,10,15,20,40) qui semble cohérente avec la problématique. Afin de vérifier que les nouvelles classes qui en résultent répondent bien aux exigences du test d'ajustement du Khi’², nous faisons un nouvel histogramme en spécifiant cette fois les bornes des intervalles des classes.

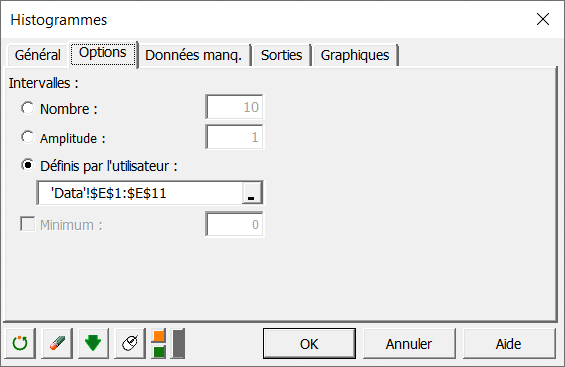
Interprétation des résultats de l'histogramme avec des intervalles spécifiées

Une fois le bouton OK cliqué, une nouvelle feuille est créée ("Histogramme1") contenant l'histogramme correspondant aux classes définies ci-dessus. Nous constatons que toutes les classes contiennent au moins 6 éléments, ce qui est en accord avec le test d'ajustement du Khi’² que nous allons utiliser ci-dessous, pour vérifier si l'échantillon suit bien une loi binomiale négative. La vidéo suivante vous montre comment l'on peut spécifier les bornes des intervalles des classes.

Test d'ajustement à la loi Binomiale négative

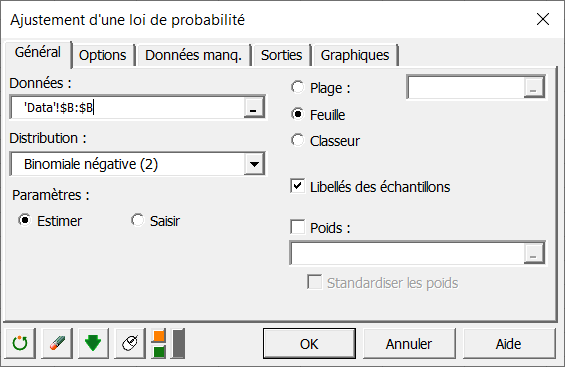
Pour ajuster une loi de probabilité à un échantillon, et tester la qualité de l'ajustement, choisissez la commande XLSTAT / Modélisation / Ajustement d'une loi de probabilité. Une fois le bouton cliqué, la boîte de dialogue apparaît. Vous pouvez alors sélectionner les données sur la feuille Données. Nous laissons XLSTAT libre d'estimer les paramètres de la loi binomiale négative. XLSTAT propose deux formulations de la loi binomiale négative. Celle qui est adaptée à ce type de données est la deuxième. 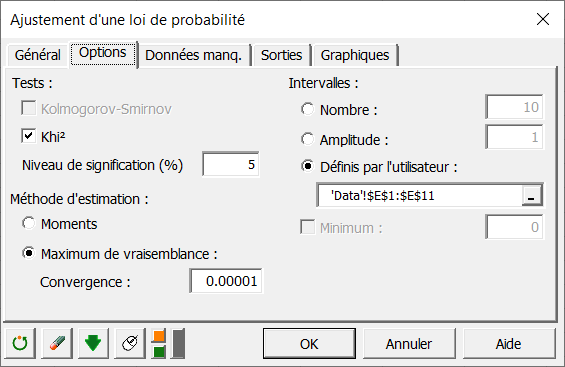Nous activons l'option de test du Khi’², nécessaire pour tester notre hypothèse. Pour le test du Khi’², nous décidons qu'il sera effectué sur les classes que nous avons précédemment créées. Dans l'onglet Graphiques, les options suivantes sont activées.

Interprétation des résultats du test d'ajustement à la loi Binomiale négative

Le premier résultat qui nous intéresse est la valeur des paramètres k et p de la loi binomiale négative (ajustée par la méthode du maximum de vraisemblance) affiché dans le tableau Paramètres estimés. Dans le tableau des statistiques estimées, on peut comparer 4 statistiques élémentaires (moyenne, variance, asymétrie, et aplatissement), calculées à partir des données, et à partir des paramètres en utilisant les propriétés de la loi choisie. 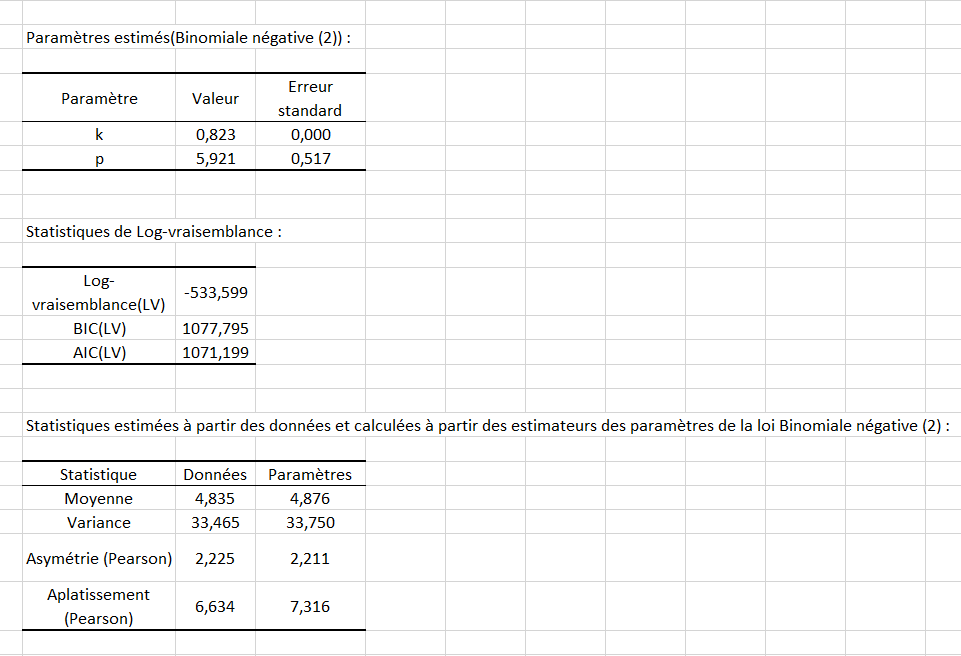Nous constatons ici que les espérances et les variances ne diffèrent pas trop, ce qui se justifie par la taille de l'échantillon et la bonne adéquation à la loi. (NB: l'espérance théorique vaut kp, et la variance théorique vaut kp(p+1)). Le test du Khi’² permet de tester si la distance du Khi’² entre la distribution empirique et la distribution théorique, calculée sur les classes, n'est pas au-delà d'une valeur critique. La comparison visuelle des histogrammes théoriques et observés est possible sur la figure suivante. 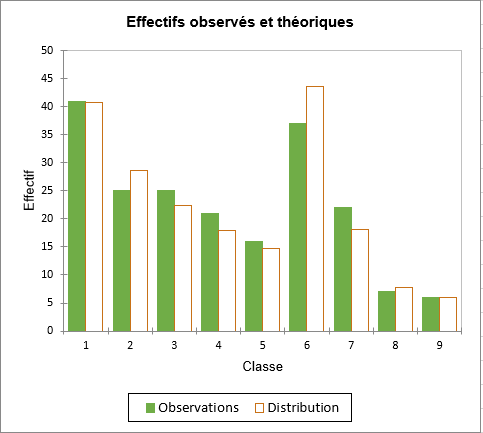Pour les classes 2,6 et 7, il semble y avoir une légère inadéquation. Malgré ces légers écarts, la p-value associée au test (0.770) est nettement supérieure au seuil de signification que l'on s'est fixé (0.05). Le test du Khi’² permet donc de confirmer l'hypothèse selon laquelle l'échantillon est distribué suivant une loi binomiale négative. En conclusion, la présence de la bactérie étudiée dans la rivière dans laquelle ont eu lieu les prélèvements, suit une loi binomiale négative de paramètres (k=0.823, p=5.921), avec une espérance de 4.8 et une variance de 33.4. La vidéo suivante vous fournira des informations complémentaires sur les histogrammes :