Régression PLS (moindres carrés partiels) dans Excel

Ce tutoriel explique comment calculer et interpréter une régression par les moindres carrés partiels dans Excel en utilisant XLSTAT.

Jeu de données pour réaliser une régression par les moindres carrés partiels - PLS

Ce tutoriel est basé sur des données qui ont été largement analysées dans [Tenenhaus, M., Pagès, J., Ambroisine L. et Guinot, C. (2005); Méthodologie PLS pour l'étude des relations entre les jugements hédoniques et les caractéristiques des produits ; Food Quality and Preference. 16, 4, pp 315-325].

Les données utilisées dans cet article correspondent à 6 jus d'orange décrits par 16 descripteurs physico-chimiques et évalués par 96 juges.

Objectif de la régression par Moindres Carrés Partiels dans cet exemple

La régression par Moindres Carrés Partiels va nous permettre d'obtenir une carte simultanée des juges, des descripteurs et des produits, puis d'analyser pour certains juges quels descripteurs sont liés à leurs préférences.

Paramétrer une régression par les moindres carrés partiels - PLS

• Une fois XLSTAT ouvert, cliquez sur Modélisation des données / Régression PLS.

• Après avoir cliqué sur le bouton, la boîte de dialogue de la régression par Moindres Carrés Partiels s'affiche.

• Dans le champ Variable(s) dépendante(s), sélectionnez avec la souris les évaluations des 96 juges.

• Les évaluations sont les "Ys" du modèle puisque nous voulons expliquer les évaluations données par les juges.

• Dans le champ Variable(s) quantitative(s), sélectionnez les variables explicatives, qui sont dans notre cas les descripteurs physico-chimiques.

• Les noms des jus d'orange ont également été sélectionnés comme Étiquettes d'observation.

• Dans l'onglet Options de la boîte de dialogue, nous fixons le nombre de composantes à 4 dans les Conditions d'arrêt.

• Enfin, dans l'onglet Graphiques, l'option Étiquettes colorées a été activée pour faciliter la lecture des graphiques. L'option Vecteurs a été décochée pour ne pas saturer les graphiques.

• Les calculs extrêmement rapides commencent lorsque vous cliquez sur OK. L'affichage des résultats est interrompu pour vous permettre de sélectionner les axes pour les cartes.

• Ensuite, dans la boîte Sélectionner les axes, il suffit de cliquer sur Terminé pour que les graphiques ne soient affichés que pour les deux premiers axes.

Interpréter les résultats d'une régression par les moindres carrés partiels - PLS

Après quelques statistiques de base sur les différentes variables sélectionnées (les variables explicatives sont en noir, et les variables dépendantes en bleu) et la matrice de corrélations correspondante, les résultats propres à la régression PLS sont affichés.

Le premier tableau et le graphique correspondant permettent de visualiser la qualité de la régression PLS en fonction du nombre de composantes retenues.

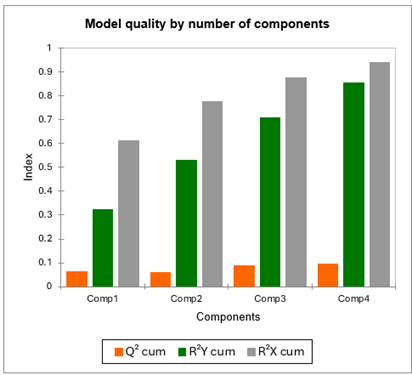
L'indice Q² cumulé est une mesure globale de la qualité de l'ajustement et de la qualité prédictive des 96 modèles. XLSTAT a retenu 4 composantes. On voit que l'indice Q² reste faible. Cela suggère que la qualité de l'ajustement peut être très variable en fonction des juges.

Les R²Y cum et R²X cum qui correspondent aux corrélations entre les composantes et les variables de départ sont proches de un dès la quatrième composante, ce qui indique que les composantes sont à la fois bien représentatives des X et des Y.

Le premier graphique des corrélations permet de visualiser sur les deux premières composantes générées par la régression PLS les corrélations entre X et les Y du modèle.

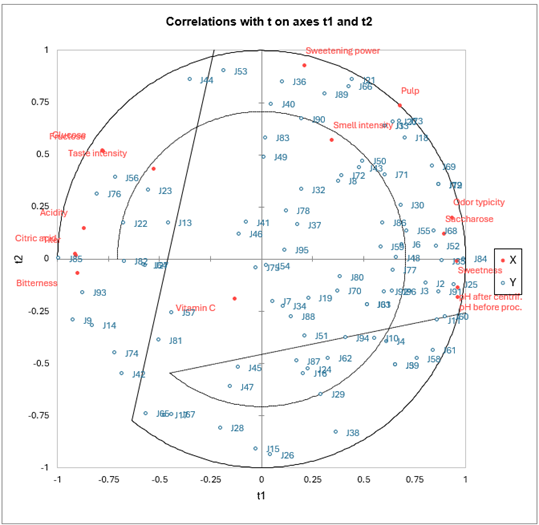
On note que pour quelques juges au centre du graphique les corrélations sont très faibles. En se reportant au tableau, on voit par exemple que le juge 54 n'est lié qu'à la composante t4, globalement peu corrélée avec les variables explicatives.

En ce qui concerne les variables explicatives, on note que seule la vitamine C est mal représentée sur le graphique. Cette dernière est donc globalement faiblement explicative des préférence des juges, ce qui se comprend bien puisque elle n'a pas d'implication directe sur les critères gustatifs qui influencent les juges.

On notera les fortes corrélations positives entre le fructose et le glucose, entre les pH, et la corrélation bien entendu négative entre les pH d'une part, et l'acide citrique et le titre d'autre part. On voit apparaître sur ce graphique une grande différence de préférences entre les juges.

La carte superposant les variables dépendantes sur les vecteurs c et les variables explicatives sur les vecteurs w* permet de visualiser la relation globale entre les variables, sachant que les w* sont représentatifs du poids des variables dans les modèles.

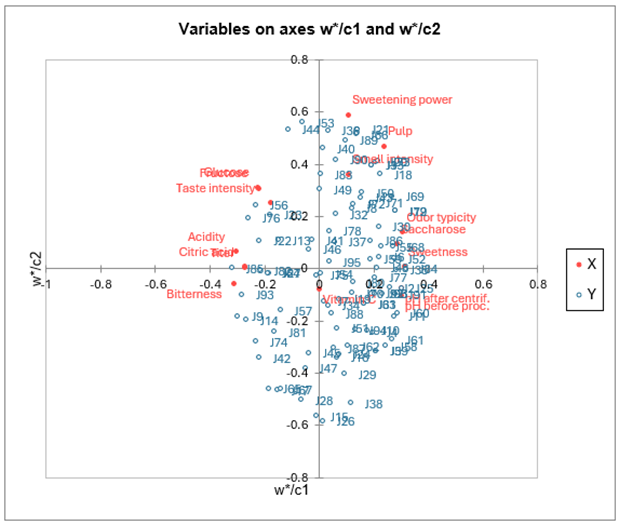
Si l'on projète une variable explicative sur le vecteur d'une variable dépendante (les vecteurs sont affichés s'il y a moins de 50 variables dépendantes et si l'option vecteurs est activée), on a une idée de son poids dans le modèle concernant cette même variable dépendante.

Un tableau donne les coordonnées des produits sur les composantes t. Le graphique correspondant sur les axes t1 et t2 est ensuite affiché. On notera que les produits sont bien distingués.

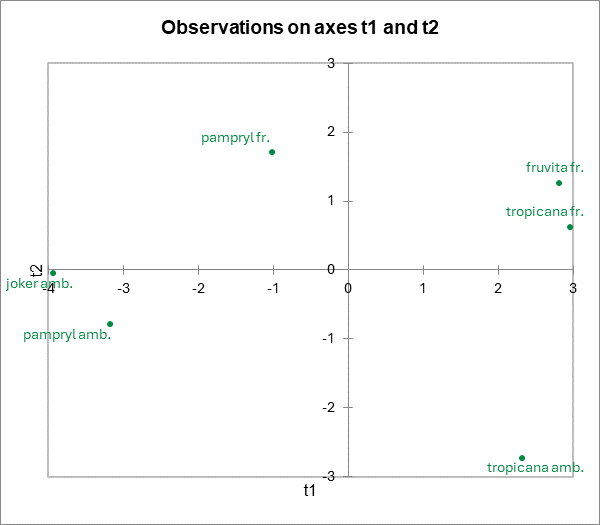
Un dernier graphique de corrélations permet de superposer les produits sur le graphique des corrélations précédemment affiché. Dans la légende, "Obs" a été remplacé manuellement par "Jus", en modifiant l'intitulé de la série dans la barre de formule Excel, après avoir cliqué sur la série pour la sélectionner. Comme presque toujours avec XLSTAT, les graphiques sont des graphiques Excel totalement modifiables.

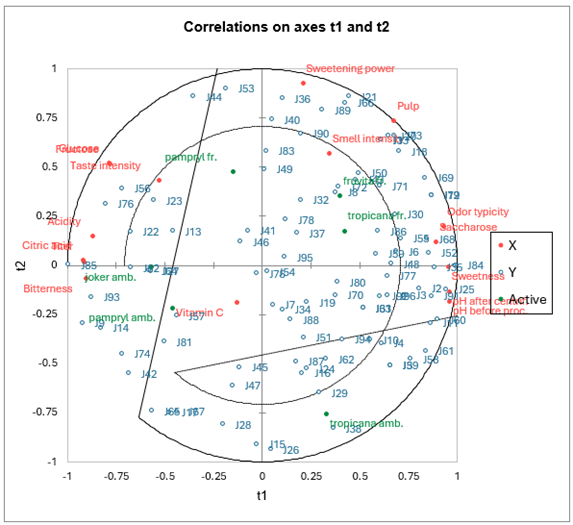
Dans leur article précédemment cité, Tenenhaus et al. interprètent ce graphique en détail. Ils en déduisent notamment l'existence de 4 groupes bien identifiés de juges, sur lesquels il conseillent de réaliser des analyses séparées. Ils obtiennent alors des Q² et R² cumulés plus élevés. Pour le premier groupe identifié ils obtiennent un R²Y de 0.63 au lieu du 0.53 observé ici.

Deux tableaux fournissant des résultats pour les composantes u et u~ sont ensuite affichés. Un graphique permet de visualiser les observations (ici les jus d'orange) dans l'espace des u~.

Les tableaux qui suivent permettent de voir l'évolution des indices Q² et Q² cumulé en fonction du nombre de composantes. pour l'ensemble des variables dépendantes. On remarque que pour plusieurs variables que le maximum du Q² est atteint avec une ou deux composantes (voir par exemple J5, J6, J7).

Une série de tableaux présentant les R² pour chacune des variables d'entrée avec les composantes t est ensuite optionnellement affichée. L'option n'étant pas activée par défaut, les tableaux ne sont pas pris en compte dans ce tutoriel.

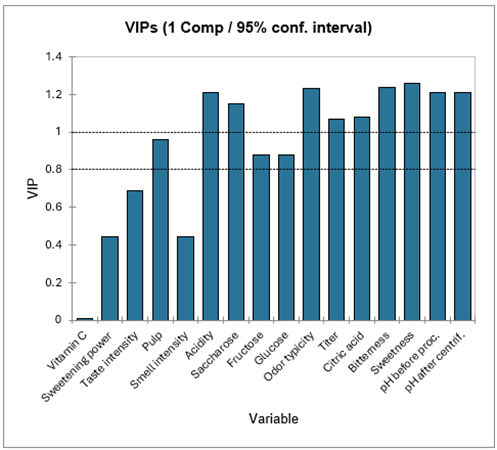
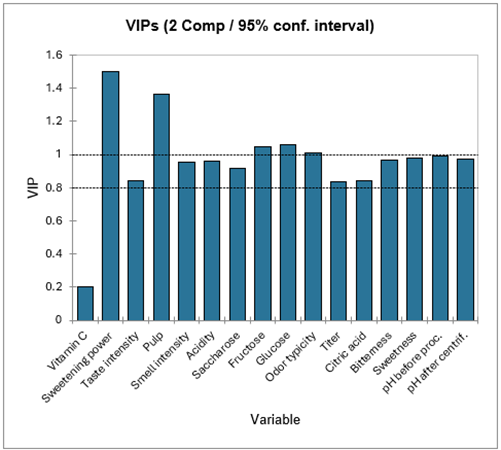
Le tableau suivant présente les VIP (Variable Importance for the Projection) pour chacune des variables explicatives, sur chacun des modèles avec un nombre croissant de composantes. Cela permet d'identifier rapidement quelles sont les variables explicatives les plus importantes sur l'ensemble des modèles. Sur la première composante, la Vitamine C, le Pouvoir Sucrant, l'Intensité Odeur et l'Intensité Goût apparaissent comme étant peu influentes.

Le tableau des paramètres des modèles correspondant à chacune des variables dépendantes est ensuite affiché. Les équations sont ensuite affichées afin de faciliter une éventuelle utilisateur ultérieure.

Pour chaque modèle sont ensuite affichés le tableau des coefficients d'ajustement, le tableau des coefficients normalisés (correspondant aux coefficients bêta de la régression linéaire classique) et enfin le tableau des prédictions et résidus. L'analyse du modèle correspondant au juge J1 nous permet de conclure à une bonne qualité du modèle, le R² vallant 0.88. Cependant, le nombre de degrés de liberté est faible (DDL =1), et on risque un sur-ajustement du modèle. Cela tend à être confirmé par le fait que pour l'ensemble des coefficients normalisés, les intervalles de confiance comprennent la valeur 0. Etant donné que le Q² cumulé diminue dès la troisième composante (cf tableau des Q²), il est fort probable qu'une qualité similaire aurait été atteinte avec seulement deux composantes.

Nous avons donc réalisé une nouvelle régression PLS, en ne sélectionnant que le juge 1, et en forçant XLSTAT à ne prendre en compte que deux composantes. Les résultats sont disponibles sur la feuille PLS2. On obtient alors des résultats plus riches. Le graphique ci-dessous correspond aux coefficients normalisés pour le modèle avec 2 composantes.

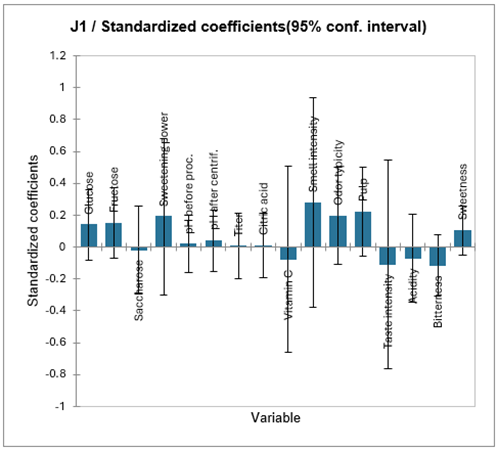
On voit ici que seuls les coefficients de l'intensité d'odeur et la typicité d'odeur sont significatifs. Le tableau des prédictions et résidus permet de vérifier que les notes du juge 1 sont très bien reproduites par le juge 1.

Enfin le tableau des DModX et DModY et les graphiques correspondant permettent d'identifier rapidement des observations qui constitueraient d'éventuels outliers (valeurs extrêmes). Ici, aucune valeur anormale n'a été détectée. Toutes les valeurs sont en effet inférieures aux DCritX et DCritY.