ANOVA déséquilibrée à deux facteurs avec interactions dans Excel
Ce tutoriel explique comment mettre en place et interpréter une analyse de variance déséquilibrée à deux facteurs dans Excel avec XLSTAT.
Jeu de données pour l'analyse de la variance ou ANOVA déséquilibrée à deux facteurs avec interactions
Les données correspondent à une expérience où trois méthodes de culture ont été testées sur quatre types de champs (mêmes sols, mais des expositions différentes).
Le rendement de la culture a été mesuré après la moisson.
Parce que la 3ième méthode n'a pu être testée sur le 4ième type de champ (manque de graines), et parce qu'une expérience n'a pu être menée à bout (méthode 2, type de champ 4) à cause d'un orage de grêle, nous nous trouvons ici dans le cas d'une ANOVA déséquilibrée. Comme l'interaction entre la méthode et le type de champ est intéressante pour l'expérimentateur, nous allons réaliser ici une ANOVA avec interactions.
But de ce tutoriel sur l'ANOVA déséquilibrée à deux facteurs avec interactions
En utilisant l'outil d'ANOVA d'XLSTAT nous cherchons ici à déterminer s'il existe une influence significative de la méthode, du type de champ, et éventuellement de leur interaction.
Paramétrer une ANOVA déséquilibrée à deux facteurs avec interactions
Une fois XLSTAT lancé, choisissez la commande XLSTAT / Modélisation / ANOVA.
Une fois le bouton cliqué, la boîte de dialogue correspondant à l'ANOVA apparaît.
Vous pouvez alors sélectionner les données sur la feuille Excel.
La Variable dépendante correspond à la variable expliquée, soit, dans ce cas précis, au "rendement" de la culture dont nous voulons expliquer la variabilité par l'effet de la "méthode", du "type de champ" et de "méthode*type de champ" (l'interaction).
L'option Libellés des variables est laissée activée car la première ligne des colonnes comprend le nom des variables.
Dans XLSTAT, il est possible de sélectionner les données de deux façons différentes pour l’ANOVA. La première est sous forme de colonne, une colonne pour la variable dépendante, une autre pour les deux variables explicatives.
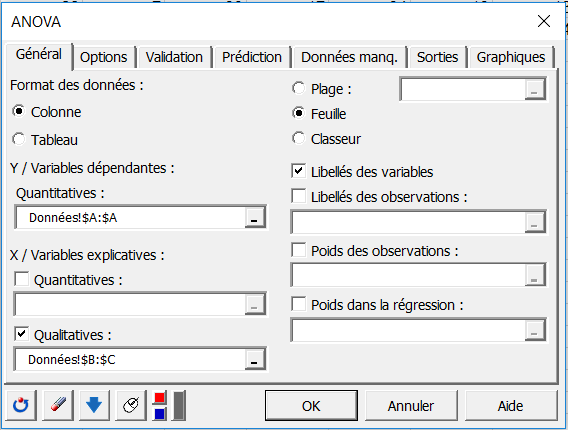
La seconde manière de sélectionner les données est sous forme de tableau, avec, en colonne, les modalités d’une variable explicative, et en lignes, les modalités de la seconde variable explicative.

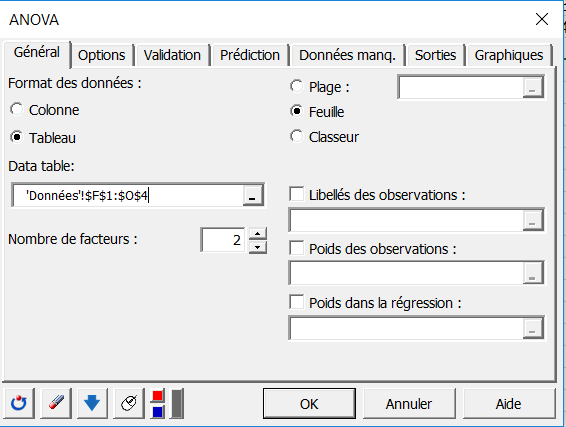
Dans l'onglet Options, l'option Interaction est activée, et le niveau maximum d'interaction est fixé à 2.
L'option de contrainte choisie est a1=0, ce qui implique que le modèle s'écrira de façon à considérer que la méthode 1 et le type de champ 1 auront l'effet de base.
Appliquer une contrainte en ANOVA est indispensable pour des raisons théoriques, mais cela ne change ni les résultats (prévisions, R’², etc.), ni la qualité de l'analyse.
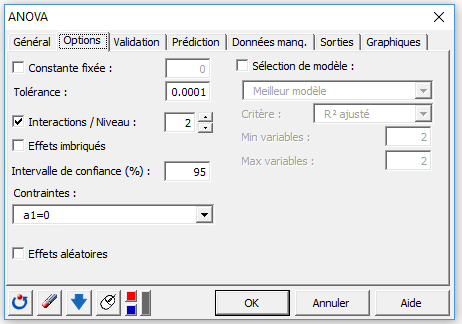
Dans l'onglet Sorties, les options Type I SS et Type III SS est activée car nous voulons analyser les tests effectués dans les tableaux correspondant (SS pour sum of squares, somme des carrés).

Une fois que vous avez cliqué sur le bouton OK, une boîte de dialogue est affichée pour que l'utilisateur puisse confirmer quels facteurs doivent être inclus dans le modèle.

Les calculs de l'ANOVA sont ensuite effectués, et les résultats sont affichés.
Interpréter les résultats d'une ANOVA déséquilibrée à deux facteurs avec interactions
Le premier tableau de résultats fournit les coefficients d'ajustement du modèle. Le R’² (coefficient de détermination) donne une idée du % de variabilité de la variable à modéliser, expliqué par les variables explicatives. Plus ce coefficient est proche de 1, meilleur est le modèle. Dans notre cas, 92% de la variabilité est expliquée par la méthode, le type de champ et l'interaction. Le reste de la variabilité est explicable par des effets qui n'ont pas été identifiés au cours de cette expérience. Ils se trouvent donc inclus dans la partie "aléatoire" du modèle.

Le tableau d'analyse de la variance est un résultat qui doit être analysé attentivement (voir ci-dessous). C'est à ce niveau que l'on teste si l'on peut considérer que les variables explicatives sélectionnées et leurs éventuelles interactions apportent une quantité d'information significative au modèle (hypothèse nulle H0) ou non. En d'autres termes, c'est un moyen de tester si la moyenne de la variable à modéliser suffirait à décrire les résultats obtenus ou non.

Le test du F de Fisher est utilisé. Etant donnée que la probabilité associée au F est de 0.0003, cela signifie que l'on prend un risque de 0.03% en concluant que la variable explicative apporte une quantité d'information significative au modèle. Nous pouvons donc conclure que les deux variables et leur interaction apportent une information significative pour expliquer la variabilité du rendement. Nous voulons maintenant savoir si les variables contribuent toutes autant à expliquer la variabilité. Pour cela nous devons analyser les tableaux de résultats Type I SS et Type III SS.

Le tableau Type I SS est construit en ajoutant les variables une à une dans le modèle, et en évaluant l'impact sur la somme des carrés du modèle. De ce fait, l'ordre dans lequel les variables sont entrées dans le modèle influe sur les résultats obtenus. Le tableau Type III SS est calculé en enlevant ponctuellement chacune des variables du modèle, toutes les autres étant présentes, afin d'évaluer l'impact de la variable supprimée sur le modèle. Ainsi, les valeurs obtenues dans le tableau Type III SS sont indépendantes de l'ordre dans lequel sont sélectionnées les variables. Le tableau Type III SS est souvent préféré pour l'analyse des résultats d'un modèle avec interactions.
Remarque : plus la somme des carrés du Modèle est élevée, plus la somme des carrés des Résidus est faible, et plus importante est l'influence de la variable sur le modèle.
Des résultats du tableau Type III SS, on peut déduire que la méthode est la variable qui apporte le plus d'information au modèle. En analysant les paramètres du modèle (voir ci-dessous) on voit que les méthodes 2 et 3 ont un effet positif sur le rendement. Le type de champ n'a pas d'effet significatif sur le modèle, l'interaction entre cette variable et la méthode a un effet significatif (au seul de 5%). Pour les prochaines analyses, les deux variables principales devront donc être conservées.
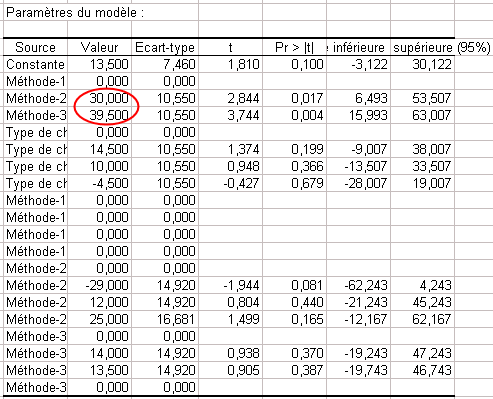
Le tableau ci-dessus peut être utilisé pour étudier l'impact des variables sur le rendement, mais aussi pour prédire des valeurs dans des situations qui n'on pas été rencontrées. Ainsi, d'après le modèle, on peut déterminer que la méthode 3 appliquée sur un type de champ 4, donnerait un rendement moyen de 48.5, tout en sachant que l'influence de l'interaction entre la méthode 4 et le type de champ 3 ne peut être prise en compte.
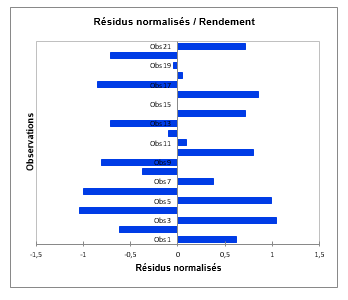
Enfin, une attention particulière doit être portée aux résidus centrés réduits, qui, étant données les hypothèses liées à l'ANOVA, doivent être distribués suivant une loi normale N(0,1). Cela signifie, entre autres, que 95% des résidus doivent se trouver dans l'intervalle [-1.96, 1.96]. Etant donné le faible nombre de données dont on dispose ici, toute valeur en dehors de cet intervalle est révélatrice d'une donnée suspecte. Nous pouvons vérifier qu'ici toutes les données sont dant l'intervalle.
Cet article vous a t-il été utile ?
- Oui
- Non