Unausgeglichene Two-Way ANOVA mit Interaktion

Dieses Tutorium wird Ihnen helfen, eine ANOVA (Analysis of Variance) mit zwei Faktoren für unausgeglichene Daten in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.

Sie sind nicht sicher, ob es sich hierbei um die Modellierungsfunktion handelt, nach der Sie suchen? Weitere Hinweise finden Sie hier.

Datensatz für eine unausgeglichene ANOVA mit zwei Faktoren mit Interaktionen in Excel

Die Daten entsprechen einem Experiment, bei dem 4 neue Methoden des Getreideanbaus auf vier verschiedenen Feldtypen getestet wurden (gleiche Böden aber unterschiedliche Lichtverhältnisse). Der Ertrag wurde nach der Ernte gemessen. Da die dritte Methode nicht auf dem vierten Feldtyp (aus Mangel an Saatgut) getestet wurde, und da die zweite Methode nicht auf dem vierten Feldtyp (aufgrund eines Hagelsturms) getestet wurde, ist dies ein typisches Beispiel einer unausgeglichenen ANOVA. Wir führen eine ANOVA mit Interaktionen durch, um die Interaktionen zwischen den Anbaumethoden und den Feldtypen zu untersuchen.

Mit der XLSTAT ANOVA Funktion, kann man herausfinden, ob die Anbaumethode einen signifikanten Einfluss auf den Ertrag durch die Kontrolle des Feldtyps und die Interaktion zwischen der Anbaumethode und dem Feldtyp.

Einrichten einer unausgeglichenen ANOVA mit zwei Faktoren mit Interaktionen

Nach dem Öffnen von XLSTAT, wählen Sie den Befehl XLSTAT/Modellierung der Daten/ANOVA.

Nach dem Klicken des Buttons erscheint das entsprechende Dialogfenster der ANOVA.

Sie können nun die Daten im Excel-Blatt auswählen.

Es gibt mehrere Arten die Daten in den XLSTAT Dialogfenstern auszuwählen (siehe auch das Tutorial Datenauswahl zu diesem Thema). Im untersuchten Beispiel beginnen die Daten in der ersten Zeile; es ist daher schneller die Spaltenauswahl zu benutzen. Daher erscheinen im Dialogfenster unten die Auswahlen in Form von Spalten.

Die Option „Variablenbeschriftungen“ ist aktiviert, da die erste Zeile der Daten die Namen der Variablen enthält. Wählen Sie die "Abhängigen Variablen" (oder Modellvariable) als die „Ertrag“. Ziel ist es, den Effekt der Anbaumethode, des Feldtyps und der Interaktion beider auf den Ertrag zu untersuchen.

In XLSTAT ist es möglich, die Daten für die ANOVA auf zwei verschiedene Arten auszuwählen. Die erste ist in Form von Spalten, eine Spalte für die abhängige Variable, eine weitere für die erklärende Variable.

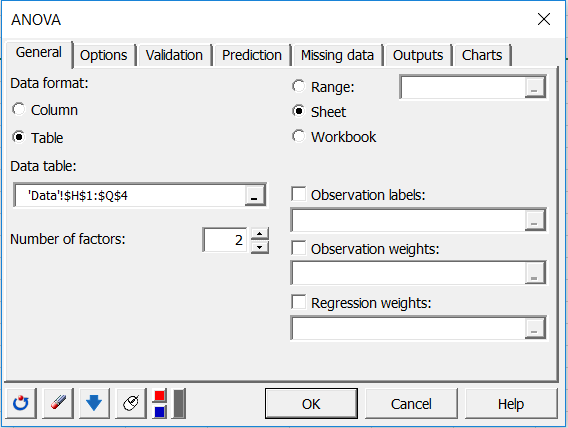
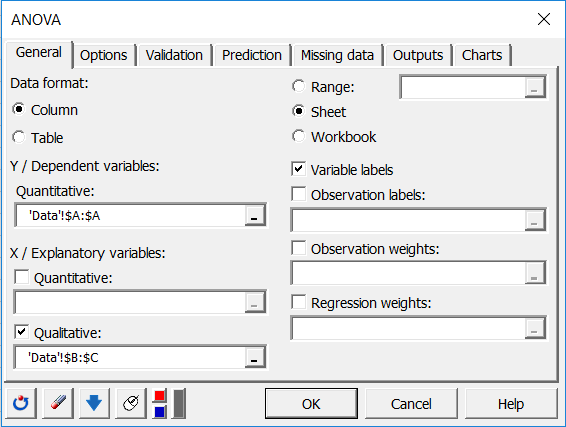Die zweite Möglichkeit, die Daten auszuwählen, besteht in Form einer Tabelle, wobei jede Spalte eine Modalität der erklärenden Variablen darstellt.

Im Reiter Optionen ist die Option "Interaktionen" aktiviert und das maximale Niveau wird als 2 gewählt.

Man lässt die Beschränkungsoption bei "a1=0", was bedeutet, dass man ein Modell auf der Prämisse erzeugt, dass die Methode "1" den Standardeffekt auf den Ertrag hat.

Das Anwenden einer Bedingung ist notwendig für ein ANOVA-Modell aus theoretischen Gründen, aber es hat keine Auswirkung auf die Ergebnisse (Anpassungsgüte, Vorhersagen). Der einzige Unterschied liegt in der Art, in der das Modell beschrieben wird.

Im Reiter "Ausgabe" aktivieren Sie die Option "Typ I SS" und "Typ III SS", da das Modell Interaktionen berücksichtigt und wie die F Werte in den Typ I SS und Typ III SS Tabellen (SS „square sum“ steht für Summe der Quadrate) zu analysieren.

Die Berechnungen beginnen, sobald der Button OK geklickt wird.

Interpretieren der Ergebnisse einer unausgeglichenen ANOVA mit zwei Faktoren mit Interaktionen

Im Dialogfenster zur Auswahl der Faktoren wählen Sie die im Modell zu berücksichtigenden Faktoren aus. Die Ergebnisse werden angezeigt. Die erste Tabelle zeigt die Koeffizienten der Anpassungsgüte des Modells an. Das R(Korrelationskoeffizient), R’² (Determinationskoeffizient) und das angepasste R’². Der Determinationskoeffizient (hier 0.92) gibt den reellen Eindruck über den Prozentsatz der Variabilität der abhängigen Variablen (hier der Ertrag) an, die durch die erklärenden Variablen beschrieben (hier die Anbaumethode, der Feldtyp und ihre Interaktion) wird. In unserem Fall wird 92% der Variabilität erklärt. Die übrigen 8% sind in anderen Variablen versteckt, die nicht verfügbar sind und die das Modell in den "Zufallseffekten" verbirgt. Es ist wichtig die Ergebnisse der Varianzanalyse-Tabelle zu untersuchen (siehe unten). Diese Ergebnisse lassen uns entscheiden, ob die erklärenden Variablen eine signifikante Information (Nullhypothese H0) in das Modell einbringen oder nicht. Mit anderen Worten ausgedrückt, ist dies eine Art zu überprüfen, ob es Sinn macht den Mittelwert zu benutzen, um die gesamte Population zu beschreiben, oder ob die Information, die von der/den erklärenden Variable(n) eingebracht wurde, wertvoll ist. Anhand der Tatsache, dass die Wahrscheinlichkeit die dem F value entspricht kleiner als 0.0003 ist, ist das Risiko kleiner als 0.03%, dass die Annahme der Nullhypothese (kein Einfluss der beiden erklärenden Variablen und ihrer Interaktion) falsch ist. Daher kann man sicher schließen, dass ein Effekt der beiden Variablen und Ihre Interaktion auf die abhängige Variable besteht. Wir möchten ebenfalls herausfinden, ob die beiden Variablen und ihre Interaktion die gleiche Information hergeben. Um dies durchzuführen, müssen wir die Tabellen Typ I SS und Typ III SS näher untersuchen. Die Tabelle Typ I SS wird erzeugt mittels Hinzufügen der Variablen einer nach der anderen in das Modell und die Berechnung der zugehörigen Effekts auf die Quadratsumme des Modells (Modell SS). Als Folge hiervon hat die Reihenfolge der Variablenauswahl einen Einfluss auf das Ergebnis. Die Tabelle Typ III SS wird berechnet mittels Entfernen von je einer Variable aus dem Modell, um den Einfluss auf die Qualität des Modells zu messen. Das heißt, dass die Reihenfolge der Variablenauswahl keinen Einfluss auf die Werte des Typ III SS hat. Die Typ III SS Tabelle wird ist im Allgemeinen die beste Methode zur Interpretation der Ergebnisse, falls eine Interaktion im Modell enthalten ist. Bemerkung: Je größer die Quadratsumme des Modells ist, desto niedriger ist die residuale Quadratsumme des Modells und desto größer der Einfluss der Variablen. Anhand der in der Tabelle Typ III SS angezeigte Ergebnisse, kann man sehen, dass die Variable „Methode“ die Variable mit dem größten Einfluss auf das Modell ist. Betrachtet man die Modellparameter (siehe unten), so kann man sehen, dass Methoden 2 und 3 einen positiven Einfluss auf den Ertrag haben. Die Variable „Feldtyp“ hat einen geringen Einfluss auf den Ertrag, aber der Einfluss der Interaktion zwischen dem Feldtyp und der Methode sollte nicht übersehen werden (der Konfidenzbereich ist 95%, was bedeutet, dass 5% Restrisiko bleiben). Die oben angezeigte Tabelle kann dazu benutzt werden, den Einfluss der erklärenden Variablen auf den Ertrag und/oder zur Vorhersage des durchschnittlichen Ertrags in einer noch nicht durch das Experiment abgedeckten Situation, wie die dritte Methode und der vierte Feldtyp, dienen. In diesem speziellen Beispiel würde der durchschnittliche Ertrag 48.5 unter Berücksichtigung des unbekannten Einflusses der Interaktion betragen. Man kann ebenfalls die reduzierten Residuen (standardisierte Residuen) genauer betrachten, die nach den Prämissen der ANOVA normalverteilt sein sollten. Dies bedeutet unter anderem, dass 95% der Residuen im Intervall [-1.96, 1.96] liegen. Alle Werte außerhalb dieses Intervalls sind potentielle Ausreißer oder deuten darauf, dass die Normalitätsannahme falsch ist. Es scheinen hier keine Ausreißer vorzuliegen, da alle Werte im Bereich [-1.96, 1.96] liegen.