Régression linéaire simple dans Excel

Ce tutoriel vous aidera à mettre en place et à interpréter une régression linéaire simple dans Excel en utilisant le logiciel XLSTAT. La régression linéaire simple est basée sur la méthode des moindres carrés.
Vous n'êtes pas sûr que ce soit la fonction de modélisation que vous recherchez ? Consultez ce guide.

Qu'est-ce qu'une régression linéaire simple ?

La régression linéaire simple permet de prédire une variable en fonction d'une autre variable, sur la base d'une relation linéaire déduite par un algorithme d'apprentissage supervisé.
Si vous cherchez à prédire une variable en fonction de plusieurs autres, n'hésitez pas à lire notre tutoriel sur la Régression linéaire multiple.

Comment réaliser une régression linéaire simple dans XLSTAT ?

Jeu de données pour réaliser une régression linéaire simple

Les données proviennent de Lewis T. and Taylor L.R. (1967). Introduction to Experimental Ecology, New York: Academic Press, Inc. Elles concernent 237 enfants, décrits par leur sexe, leur âge en mois, leur taille en inch (1 inch = 2.54 cm), et leur poids en livres (1 livre = 0.45 kg).

But de ce tutoriel sur la régression linéaire simple

En utilisant la régression linéaire simple, notre but est d'étudier comment le poids varie en fonction de la taille, et si une relation linéaire a un sens. Il s'agit ici d'une régression linéaire simple, car une seule variable explicative est utilisée (la taille).

Cet exemple est repris dans notre tutoriel sur la régression linéaire multiple afin d'étudier l'influence de l'âge sur cette relation.

Cet ensemble de données est également utilisé dans notre tutoriel sur l'ANCOVA, afin d'ajouter le sexe (variable qualitative) comme variable explicative.

Paramétrer une régression linéaire simple

• Ouvrir XLSTAT

• Lancer la commande XLSTAT > Modélisation > Régression linéaire. Une fois le bouton cliqué, la boîte de dialogue correspondant à la régression apparaît.

• Sélectionner ensuite les données sur la feuille Excel. La Variable dépendante correspond à la variable expliquée (ou variable à modéliser), qui est dans ce cas précis le "poids". La variable quantitative explicative est ici la "taille". On veut ici expliquer la variabilité du poids par celle de la taille.

• Activer l'option Libellés des colonnes car la première ligne des colonnes comprend le nom des variables.

• Cliquer sur le bouton OK pour lancer les calculs.

Interpréter les résultats de la régression linéaire simple

Le premier tableau de résultats fournit les coefficients d'ajustement du modèle. Le R² (coefficient de détermination) donne une idée du % de variabilité de la variable à modéliser, expliqué par la variable explicative. Plus ce coefficient est proche de 1, meilleur est le modèle.

Dans notre cas, 60% de la variabilité du poids est expliquée par la taille. Le reste de la variabilité est dû à des effets (autres variables explicatives) qui ne sont pas pris en compte dans cet exemple.

Le tableau d'analyse de la variance est un résultat qui doit être analysé attentivement (voir ci-dessous). C'est à ce niveau que l'on teste si l'on peut considérer que la variable explicative sélectionnée (la taille) apporte une quantité d'information significative au modèle (hypothèse nulle H0) ou non. En d'autres termes, c'est un moyen de tester si la moyenne de la variable à modéliser (le poids) suffirait à décrire les résultats obtenus ou non.

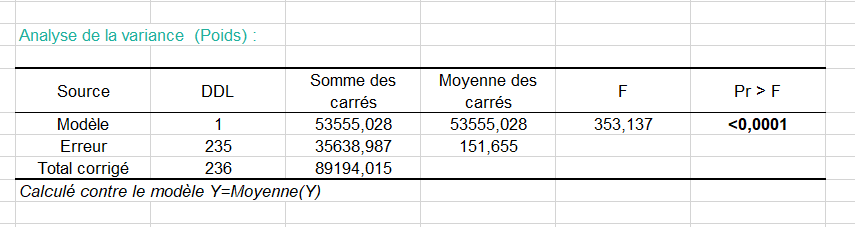
Le test du F de Fisher est utilisé. Étant donné que la probabilité associée au F est dans ce cas inférieure à 0.0001, cela signifie que l'on prend un risque de se tromper de moins de 0.01% en concluant que la variable explicative apporte une quantité d'information significative au modèle.

Le tableau suivant fournit les détails sur le modèle et est essentiel dès lors que le modèle doit être utilisé pour faire des prévisions, des simulations ou s'il doit être comparé à d'autres résultats, par exemple les coefficients que l'on obtiendrait pour les garçons. Nous voyons que si le paramètre de la taille a un intervalle de confiance assez étroit, celui de la constante du modèle est assez large. L'équation du modèle est donnée sous le tableau. Le modèle indique que dans les limites de l'intervalle de variation de la variable taille données par les observations, à chaque fois que la taille augmente d'un inch, le poids augmente de 3,8 livres.

Le tableau qui suit ensuite présente l'analyse des résidus. Une attention particulière doit être portée aux résidus centrés réduits, qui, étant donné les hypothèses liées à la régression linéaire, doivent être distribués suivant une loi normale N(0,1). Cela signifie, entre autres, que 95% des résidus doivent se trouver dans l'intervalle [-1.96, 1.96]. Étant donné le faible nombre de données dont on dispose ici, toute valeur en dehors de cet intervalle est révélatrice d'une donnée suspecte.

Afin de mettre en évidence rapidement les valeurs se trouvant hors de l'intervalle [-1.96, 1.96], nous avons utilisé l'outil DataFlagger de XLSTAT (menu Outils). Sur les 237 observations, neuf d'entre elles (38, 52, 69, 77, 108, 169, 179, 207, 224) sont hors de l'intervalle [-1.96, 1.96]. Cette analyse des résidus n'invalide donc pas l'hypothèse de normalité.

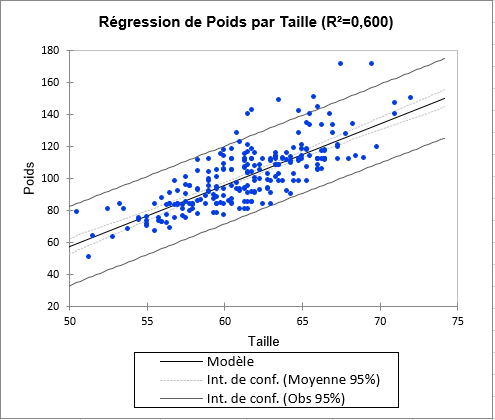
Le premier graphique permet de visualiser les données, la droite de régression, et les deux intervalles de confiance (le plus proche de la courbe est l'intervalle autour de la moyenne de l'estimateur, le second est l'intervalle autour de l'estimation ponctuelle aussi appelé intervalle de prédiction). On voit ainsi clairement une tendance linéaire, mais avec une forte variabilité autour de la droite. Nous pouvons également voir que les 9 observations qui sont en dehors de l'intervalle [-1,96, 1,96] sont également en dehors du second intervalle de confiance.

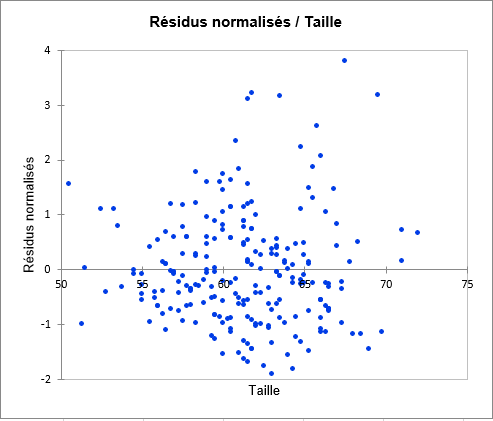
Le troisième graphique semble indiquer que les résidus croissent en fonction du poids.

Le graphique suivant permet de comparer les prévisions aux valeurs observées. Les limites de confiance permettent, comme pour le graphique de régression présenté ci-dessus, d'identifier les valeurs extrêmes.

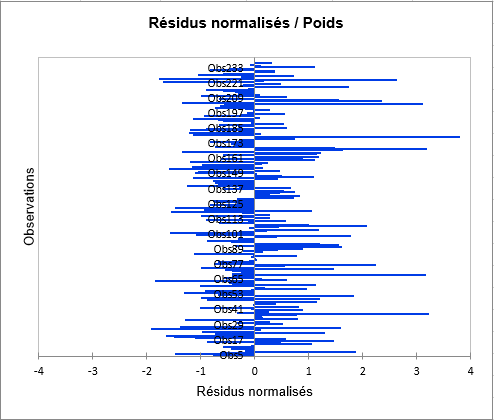
L'histogramme des résidus centrés réduits permet quant à lui de repérer rapidement et visuellement la présence de valeurs hors de l'intervalle [-2, 2].

Conclusion de la régression linéaire simple dans XLSTAT

En conclusion, la taille permet d'expliquer 60% de la variabilité du poids. Pour expliquer la variabilité restante, d'autres sources de variabilité doivent donc être prises en compte dans le modèle. Dans le tutoriel sur la régression linéaire multiple, l'âge est ajouté comme seconde variable explicative.