Tri à plat, mode & diagramme en bâtons sous Excel

Ce tutoriel explique comment décrire une variable qualitative (aussi appelée catégorielle ou nominale) en utilisant des statistiques descriptives, notamment le tri à plat, le mode et le diagramme en bâtons sous Excel avec XLSTAT.

Jeu de données pour calculer des statistiques descriptives sur une variable qualitative

Les données correspondent aux résultats d’une enquête sur le moyen de déplacement utilisé pour le trajet domicile-travail dans deux villes A et B. Les répondants sont représentés en lignes et le moyen de transport ainsi que le nom de la ville sont représentés en colonnes.

Dans cet exemple, les variables Ville et Moyen de transport sont des variables qualitatives, également appelées catégorielles ou nominales. Les valeurs d’une telle variable sont appelées modalités, catégories ou niveaux (bus, voiture par exemple dans le cas de la variable moyen de transport).

Le but de ce tutoriel est de résumer les résultats de l’enquête par ville en utilisant les statistiques descriptives et les graphiques les plus courants :

A) Statistiques descriptives :

1. Le mode qui reflète la modalité la plus fréquente, à savoir le moyen de transport le plus populaire.

2. L’effectif par modalité qui est la fréquence de chacune des modalités. Autrement dit, combien de répondants utilisent un moyen de transport spécifique.

3. La fréquence par modalité (%) qui est la fréquence relative de chacune des modalités effectif par modalité divisé par l’effectif total). Concrètement, quel pourcentage parmi l’ensemble de répondants utilise un moyen de transport spécifique.

Les statistiques 2. et 3. sont également appelées tri à plat.

B) Le Diagramme en bâtons et les barres empilées sont utilisés pour visualiser les fréquences par modalités de deux sous-échantillons (villes).

Dans cet objectif, nous utiliserons la fonction Statistiques Descriptives de XLSTAT. Cet outil nous permettra de produire les statistiques et les graphiques ci-dessus pour chaque sous-échantillons afin de détecter des différences entre les deux villes.

Paramétrer la boite de dialogue des statistiques descriptives

1. Une fois XLSTAT lancé, sélectionnez le menu XLSTAT / Description de donnes / Statistiques Descriptives.

2. La boîte de dialogue Statistiques Descriptives apparaît.

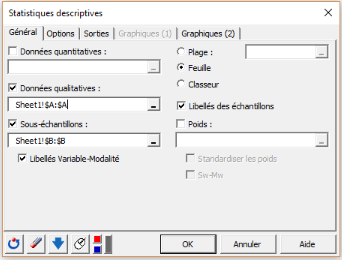
3. Dans l’onglet Général, sélectionnez la colonne Transport dans le champ Données qualitatives et la colonne Ville dans le champ Sous-échantillons afin de résumer les données par ville.

Activez également l’option Libellés Variable-Modalité afin d’afficher des libellés longs dans les sorties.

Ensuite, choisissez l'option Feuille pour que l'affichage des résultats soit effectué sur une nouvelle feuille du même classeur. Cochez également l'option Libellés des échantillons puisque le nom des variables est inclus dans la sélection.

4. Dans l'onglet Options, activez les options suivantes :

5. Dans l’onglet Sorties, sélectionnez les statistiques suivantes : Nb. d'observations, Nb. de modalités, Mode, Mode (effectif), Modalités, Effectif par modalité, Fréquence par modalité (%).

6. Dans l’onglet Graphiques(2), sélectionnez les option suivantes :

Le premier graphique permet de représenter sous forme de diagrammes en bâtons les effectifs ou les fréquences des différentes modalités (vélo, bus, etc.). Ici nous avons choisi de visualiser les fréquences.

Nous voulons également afficher des diagrammes à barres empilées pour illustrer les différences au sein de chaque sous-échantillon (ville).

Interpréter les résultats

Interpréter les statistiques descriptives d’une variable qualitative

Les résultats sont affichés dans une nouvelle feuille nommée Desc (voir ci-dessous).

Le tableau ci-dessus présente les informations suivantes pour chacun des sous échantillons (ville A et B) :

• Le nombre d’observations : 50 observations par sous-échantillon, donc 50 individus de chaque ville ont participé à l’enquête.

• Le nombre de modalités : 5 différents moyens de transport apparaissent dans les réponses.

• Le mode et l’effectif du mode : Les habitants de la ville A se déplacent surtout à vélo (=mode avec effectif égal à 21) pour aller au travail. Les habitants de la ville B préfèrent le métro (=mode avec effectif égal à 26).

• Les modalités : Les cinq moyens de transport de l’enquête sont le vélo, à pieds, le métro, la voiture et le bus.

• L’effectif par modalité : Plus d’individus de la ville B que de la ville A se déplacent en bus pour travailler (12 vs 2).

• La fréquence par modalité (%) : 42% de répondants de la ville A préfèrent le vélo tandis que seulement 3% préfèrent la voiture.

Interpréter un diagramme en bâtons et un diagramme à barres empilées

• Diagramme en bâtons

Les deux graphiques ci-dessous permettent de visualiser les fréquences relatives (fréquence en %) par modalité et par sous-échantillon. Chaque bâton représente la fréquence relative d’une modalité. Le bâton le plus haut correspond au mode.

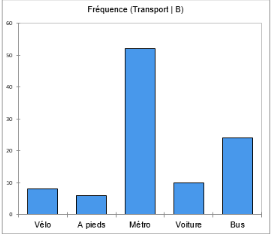
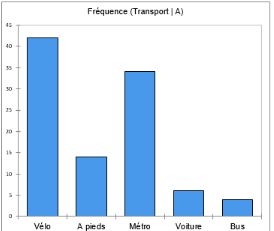
Le premier graphique nous confirme que le vélo est la modalité-mode pour la ville A avec une fréquence relative de plus de 40%. Le deuxième graphique indique que plus de 70% d’individus de la ville B se déplacent en transport en commun pour aller au travail (plus de 50% en métro et plus de 20% en bus).

Une interprétation possible est que la ville A est plus adaptée aux cyclistes ou que les habitants de la ville B travaillent loin de leur domicile donc le déplacement à vélo ou à pieds n’est pas le premier choix.

• Diagramme à barres empilées

L’avantage de ce diagramme est qu’il nous permet de visualiser la composition de plusieurs sous-échantillons en un seul graphique. Comme pour les diagrammes en bâtons, ici, nous utilisons les fréquences en pourcentages donc la longueur totale de chaque barre est la même.

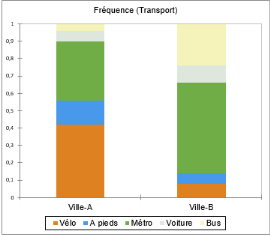
La barre de la ville A reflète le fait que le vélo, et dans une moindre mesure, le métro sont les moyens de transport privilégiés tandis que la voiture et le bus ne sont que très peu utilisés. Au contraire, la barre correspondant à la ville B montre que la majorité des habitants effectuent le trajet domicile-travail en métro (partie verte) tandis que peu de gens se déplacent à pieds (partie bleue).

Aller plus loin : utiliser un tableau de contingence (tri croisé) pour étudier l’association de deux variables qualitatives

Le tableau de contingence, aussi appelle tri croisé, est une méthode qui permet de résumer la relation entre deux variables qualitatives. XLSTAT offre un outil qui génère un tableau de contingence avec une vue 3D du tableau et calcule également des indices statistiques pour caractériser la relation entre les deux variables. Voici comment réaliser un tableau de contingence ou tri croisé avec XLSTAT.

La vidéo suivante vous fournira des informations complémentaires sur les statistiques descriptives de données qualitatives.