Penalty analysis in Excel tutorial

This tutorial helps you set up and interpret a penalty analysis in Excel using the XLSTAT statistical software.

What is Penalty analysis?

Penalty analysis is a method used in sensory data analysis to identify potential directions for the improvement of products, on the basis of surveys performed on consumers or experts. Two types of data are used:

• Preference data (or liking scores) that correspond to a global satisfaction index for a product (for example, liking scores on a 9 point scale for a chocolate bar), or for a characteristic of a product (for example, the comfort of a car rated from 1 to 10).
• Data collected on a JAR (Just About Right) 5 point scale. These correspond to ratings ranging from 1 to 5 for one or more characteristics of the product of interest. 1 corresponds not «’Not enough at all’», 2 to «’Not enough’», 3 to «’JAR’»’ (Just About Right), an ideal for the consumer, 4 to «’Too much’» and 5 to «’Far too much’». For example, for a chocolate bar, one can rate the bitterness, and for the comfort of the car, the sound volume of the engine.

The method, based on multiple comparisons such as those used in ANOVA, consists in identifying, for each characteristic studied on the JAR scale, if the rankings on the JAR scale are related to significantly different results in the liking scores.

Dataset to run a penalty analysis

Our goal is to identify some possible directions for the development of a new product.

Setting up a penalty analysis

After opening XLSTAT, select the XLSTAT / Sensory data analysis / Penalty analysis command, or click on the corresponding button of the XLSTAT-Sensory data analysis​ toolbar (see below).

Once you've clicked the button, the dialog box appears. We select the liking scores, and then the JAR data. The 3 levels JAR labels are also selected. They make the results easier to interpret.

In the Options tab, we define the threshold of the sample size below which the comparison tests won't be performed because they might not be reliable enough.

The following output options have been selected. The Spearman correlation was chosen because the data are ordinal.

The computations begin once you have clicked OK. The results will then be displayed.

Interpreting the results of a penalty analysis

The first results are the descriptive statistics for the liking data and the various JAR variables. The correlation matrix is then displayed.

The correlations between the liking and JAR variables should not be interpreted as the ranks of the JAR data are not true ordinal data (5 is less than 3 on the JAR scale, while 5 is more than 3 on the liking scale).

However if a correlation between a JAR variable and a liking variable is significantly different from 0, which could mean that the JAR variable has a low impact on the liking: if it had a strong impact, the correlation should ideally be 0. If the "too much" cases have a lower impact than the "too little", the correlation might be positive, and vice-versa for the negative correlations.

The next table is a summary of the JAR data. The chart that follows is based on that table and allows visualizing quickly how the JAR scores are distributed for each dimension.

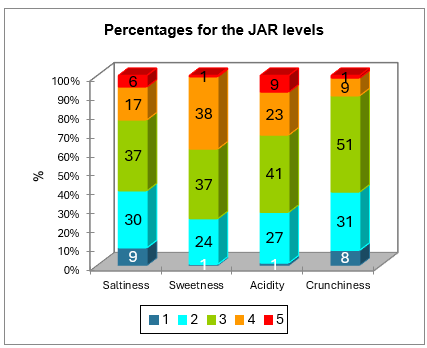
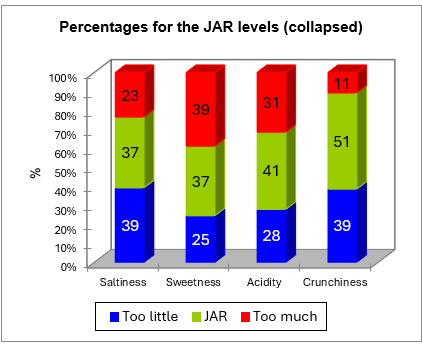
The data are then aggregated into a 3 levels scale. The corresponding frequencies table and chart are displayed below.

The next table corresponds to the penalty analysis.

The following information is displayed for each JAR dimension:

• The name of the JAR dimension.
• The 3 collapsed levels of the JAR data.
• The frequencies corresponding to each level.
• The % corresponding to each level.
• The sum of the liking scores corresponding to each level.
• The average liking for each level.
• The mean drops for the "too much" and "too little" levels (this is the difference between the liking mean for the JAR levels minus the "too much" or "too little" levels. This information is interesting as it shows how many points of liking you lose for having a product "too much" or "too little" for a consumer.
• The standardized differences are intermediate statistic that is then used for the comparison tests.
• The p-values correspond to the comparison test of the mean for the JAR level and the means for the two other levels (this is a multiple comparison with 3 groups).
• An interpretation is then automatically provided, and depends on the selected significance level (here 5%).
• The penalty is then computed. It is a weighted difference between the means (Mean of Liking for JAR - Mean of Liking for the two other levels taken together). This statistic has given its name to the method. It shows how many points of liking you lose for not being as expected by the consumer.
• The standardized difference is an intermediate statistic that is then used for the comparison test.
• The p-value corresponds to the comparison test of the mean for the JAR level with the mean of the other levels. This is equivalent to testing if the penalty is significantly different from 0 or not.
• An interpretation is then automatically provided, and depends on the selected significance level (here 5%).

For the saltiness dimension, we see that the customers strongly penalize the product when they consider it not salty enough. Both mean drops are significantly different from 0, and so is the overall penalty.

For the sweetness dimension, none of the tests is significant.

For the acidity dimension, the overall penalty is slightly significant, although the two mean drops are not. This means that acidity does matter for the customers, but this survey may not have been powerful enough to detect which specific mean drop (not enough acid and/or too acid) is concerned.

For the crunchiness, the mean drops test could not be computed for the "too much" level because the % of cases in this level is lower than the 20% threshold set earlier. When the product is not crunchy enough, the product is highly penalized.

The next two charts summarize the results described above. When a bar is red it means the difference is significant, when it is green, the difference is not significant, and when it is grey, the test was not computed because there were not enough cases.