Diskriminanzanalysen in Excel - Anleitung
Dieses Tutorium wird Ihnen helfen, eine Diskriminanzanalyse (DA) in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.
Datensatz für die Durchführung einer Diskriminanzanalyse
Die Daten stammen von [Fisher M. (1936). The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7, pp 179 -188] und entsprechen 150 Schwerlilienblüten, beschrieben durch vier Variablen (Kelchblattlänge, Kelchblattbreite, Blütenblattlänge und Blütenblattbreite) und Ihrer Spezies. Drei verschiedene Spezies wurden in die Studie einbezogen: Setosa, Versicolor und Virginica.
Absicht dieser Diskriminanzanalyse
Das Ziel ist es, zu überprüfen, ob die vier Variablen das Diskrimieren der Spezies erlauben und die Beobachtungen in einer 2-dimensionalen Karte darzustellen, die so gut wie möglich die Unterscheidung der Gruppen anzeigt.



Iris Setosa, Versicolor und Virginica.
Einrichten einer Diskriminanzanalyse
-
Nach dem Öffnen von XLSTAT, wählen Sie den Befehl XLSTAT/Analyse der Daten /Diskriminanzanalyse.
-
Nach dem Klicken des Buttons erscheint das Dialogfenster der Diskriminanzanalyse.
-
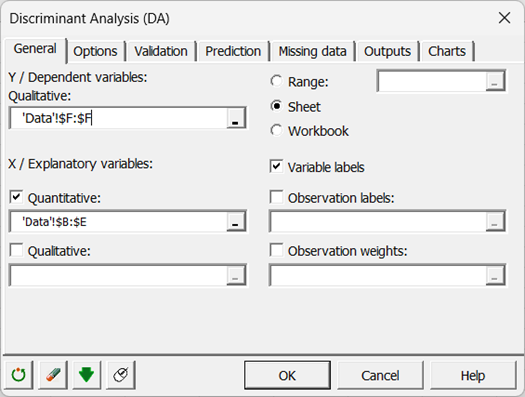
Die „abhängige Variable“ entspricht in diesem Fall der Spezies-Variablen.
-
Die “erklärenden Variablen” sind die vier beschreibenden Variablen.
-
Die “Beobachtungsbeschriftungen” werden mit dem entsprechenden Feld ausgewählt.
-
Im Options-Tab deaktivieren wir die Option Gleichheit der Kovarianzmatrizen, da, wie wir mit dem Box-Test sehen werden, die Annahme, dass die Kovarianzmatrizen der drei Arten gleich sind, falsch wäre.
-
Um zu vermeiden, dass zu viele Informationen in den Diagrammen angezeigt werden, haben wir die Option Beschriftungen im Diagramm-Tab deaktiviert.
-
Die Berechnungen beginnen, sobald Sie auf OK geklickt haben. Die Ergebnisse werden dann angezeigt.
Interpretieren der Ergebnisse einer Diskriminanzanalyse
Nach der Auswahl der beiden anzuzeigenden Achsen, die einfach durch Klicken auf „Beenden“ ausgewählt werden, werden die Ergebnisse angezeigt. Zunächst werden die verschiedenen Matrizen, die während den Berechnungen benutzt werden, angezeigt. Die beiden Box-Test bestätigen die Annahme, dass die Hypothese gleicher Kovarianzmatrizen in den verschiedenen Gruppen zurückgewiesen werden muss.


Der Wilk's Lambda-Test erlaubt es, zu überprüfen of der Vector der Mittelwerte für die verschiedenen Gruppen gleich ist oder nicht (Dies kann als multidimensionelle Variante des Fisher's LSD oder des Tukey's HSD Tests angesehen werden.). Man erkennt, dass die Unterschiede zwischen den verschiedenen Mittelwertvektoren der Gruppen signifikant ist.

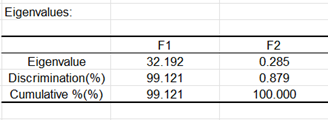
Die nächste Tabelle zeigt die Eigenwerte und die zugehörigen Varianzprozentsätze an. Man kann sehen, dass 99% der Varianz durch den ersten Faktor erklärt wird. Es gibt nur zwei Faktoren: Die maximale Anzahl an Faktoren ist gleich k-1, mit n>p>k, wobei n die Anzahl der Beobachtungen, p die Anzahl der erklärenden Variablen und k die Anzahl der Gruppen ist.
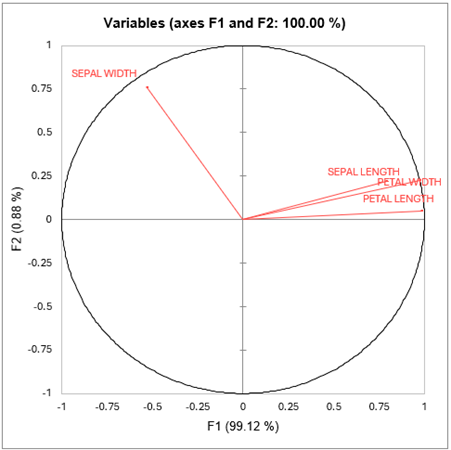
Die folgende Grafik stellt die Korrelation der Ausgangsvariablen zu den beiden Faktoren dar ( Diese Grafik entspricht der Faktorladungstabelle.). Man kann erkennen, dass der Faktor F1 mit der Kelchblattlänge, der Blütenblattlänge und der Blütenblattbreite korreliert. Der Faktor F2 ist mit der Kelchblattbreite korreliert.
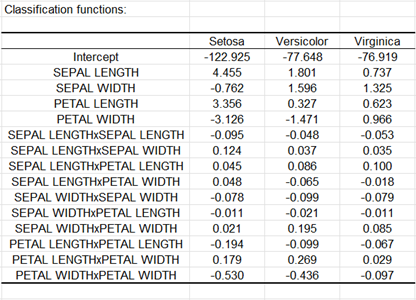
Die folgende Tabelle zeigt die Diskriminanzfunktionen an. Wenn man die Gleichheit der Kovarianzmatrix unterstellt, so sind die zugehörigen Diskriminanzfunktionen linear. Wenn keine Gleichheit der Kovarianzmatrizen unterstellt wird, welches der Fall in diesem Tutoriel ist, so sind die Diskriminanzfunktionen quadratisch. Die Regel basierend auf diesen Funktionen ist die Zuordnung einer Beobachtung zu der Gruppe, deren entsprechende Diskriminanzfunktion den grössten Wert aufweist. Diese Funktionen können ebenfalls in einem Vorhersagemodus auf neue Beobachtungen angewandt werden.
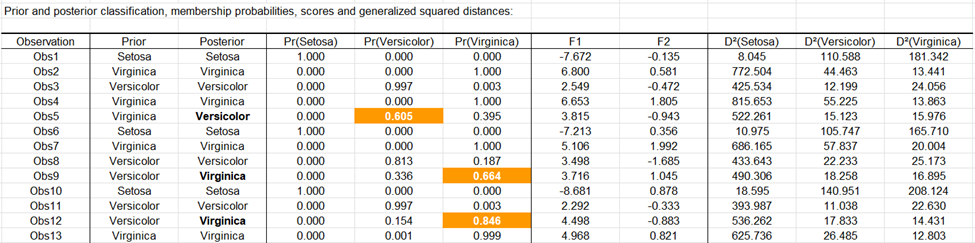
Die nächste Tabelle listet für jede Beobachtung die Faktorscores (die Koordinaten der Beobachtungen im neuen Faktorraum), die Wahrscheinlichkeit der Zugehörigkeit zu jeder der Gruppen und der quadratische Mahalanobisabstand vom Gruppenzentroid. Jede Beobachtung wird der Gruppe zugeordnet, deren Zugehörigkeitswahrscheinlichkeit am grössten ist. Die Wahrscheinlichkeiten sind ex post Werte, die die a priori Zugehörigkeitswahrscheinlichkeiten nach der Bayes Formel berücksichtigen. Man kann sehen, dass drei Beobachtungen (5,9 und 12) erneut klassifiziert wurden. Es verschiedene Interpretationsmöglichkeiten der Ergebnisse: Zum einen könnte die Person, die die Messungen vornahm Fehler bei der Aufzeichnung der Werte begangen haben oder die entsprechenden Schwertlilienblüten hatten einen ungewöhnlichen Wuchs oder die Kriterien des Spezialisten zur Bestimmung der Spezies sind nicht präzise genug oder noch notwendige Informationen zur Diskriminierung der Blumen sind in diesem Fall nicht verfügbar.
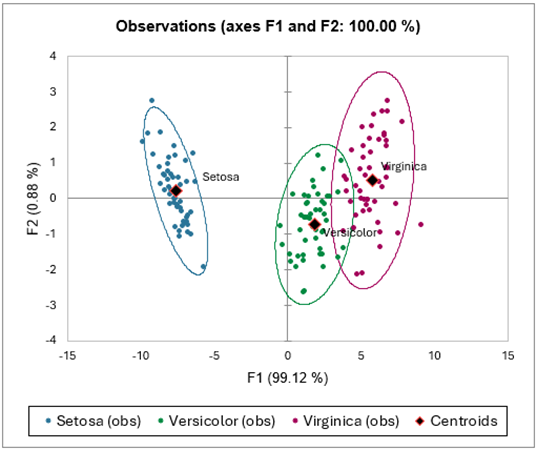
Die folgenden Grafiken stellen die Beobachtungen auf den Faktorachsen dar. Dies erlaubt es zu überprüfen, ob alle Spezies gut diskriminiert auf den Faktorachsen extrahiert aus den Ausgangsvariablen wurden.
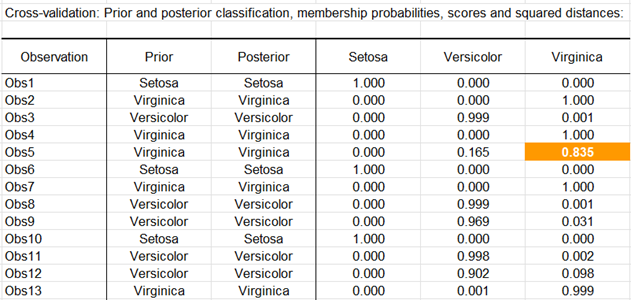
Da die entsprechende Option im Tab „Ausgaben“ des Dialogfelds aktiviert wurde, werden die Vorhersagen für die Kreuzvalidierung berechnet. Die Kreuzvalidierung ermöglicht es zu sehen, was die Vorhersage für eine bestimmte Beobachtung wäre, wenn diese aus der Schätzstichprobe ausgeschlossen würde. Wir sehen hier, dass nur eine weitere Beobachtung (Obs5) falsch klassifiziert ist.
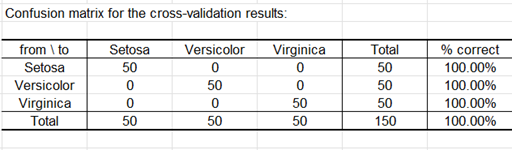
Die Verwechslungsmatrix der Kreuzvalidierung wird unten angezeigt.
War dieser Artikel nützlich?
- Ja
- Nein